.png&blockId=04a8d577-ace8-4bac-bec8-3da8a3f63bbd)
회귀 분석에서 사용된 모형의 일부 설명 변수가 다른 설명 변수와 상관 정도가 높아, 데이터 분석 시 부정적인 영향을 미치는 현상 @Jinyeop Kang @Jihyun Choi @2022년 8월 5일
•
회귀 분석의 전제 가정인 독립 변수들 간의 상관 관계가 높으면 안된다는 조건을 위배하고 동시에 모델에 포함될 때 발생
•
다중 공선성이 있다면 상관 관계가 높지만 상관 관계가 높다고 다중 공선성이 반드시 있는 것은 아님
다중공선성 정의
예시: 음주가 학업 성취도에 미치는 영향
•
종속 변수 Y : 학업 성취도
•
독립 변수 X1 : 일평균 음주량
•
독립 변수 X2 : 혈중 알코올 농도
→ 일평균 음주량이나 혈중 알코올 농도가 높을수록 학업 성취도가 낮아질 것으로 추측되기 때문에
X1과 X2 각각은 독립(설명) 변수가 되기에 적합해 보이지만 이 두 변수의 관계가 서로 독립적이지 않고 오히려 높은 상관 관계를 가지기 때문에 적합하지 않음
(일평균 음주량이 높으면 혈중 알코올 농도도 높을 것이기 때문)
이대로 회귀 분석 한다면?
X1과 X2 중 하나는 유의미한 변수로 나타나지만 다른 하나는 굉장히 불안정한 계숫값을 가질 것
회귀 분석 예시
y = a + b1x1 + b2x2 + b3x3
왜 다중 공선성이 문제인가?
•
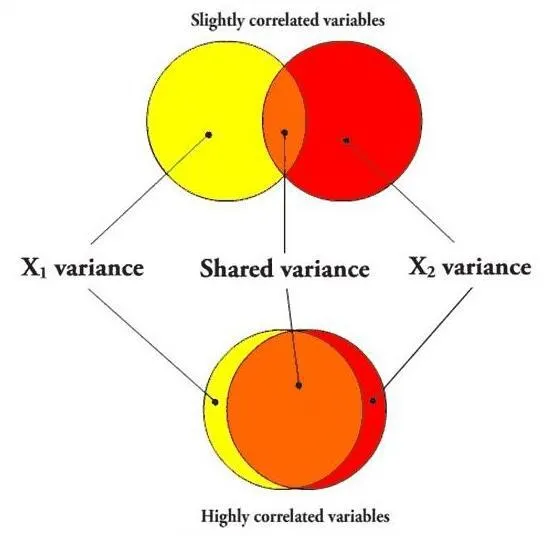
다중 공선성은 독립 변수의 설명이 겹치는 것이며, 극단적으로 상관관계가 높은 독립 변수는 중복과 같이 간주 → 모델의 과적합(overfitting) 야기
•
겹치는 면적이 커지면 다중 공선성이 높은거고 작으면 낮은거임.
•
물론 모든 변수가 완벽히 다중 공선성이 0일 수는 없음.
•
만약 두 변수가 완벽하게 다중 공선성에 걸려있으면 즉, x1 = b2x2라면 같은 변수를 두 번 넣은 것이고 최소 제곱법 계산상 어려움.
•
회귀 계수의 표준 오차(Standard Error)가 비정상적으로 증가함(=예측값의 신뢰 구간이 넓게 형성)
◦
회귀 분석 시 모든 독립 변수들 각각이 종속 변수를 정확히 설명해주기를 바람.
◦
하지만 위의 상황의 경우 X1이 설명하는 부분을 X2 또한 설명해줌.
◦
회귀 모형에서도 마찬가지로 다중 공선성이 생기면 해당되는 변수들의 설명력이 약해져서 표준 오차(Standard Error)의 증가로 드러나게 됨.
다중 공선성 판단 방법
1.
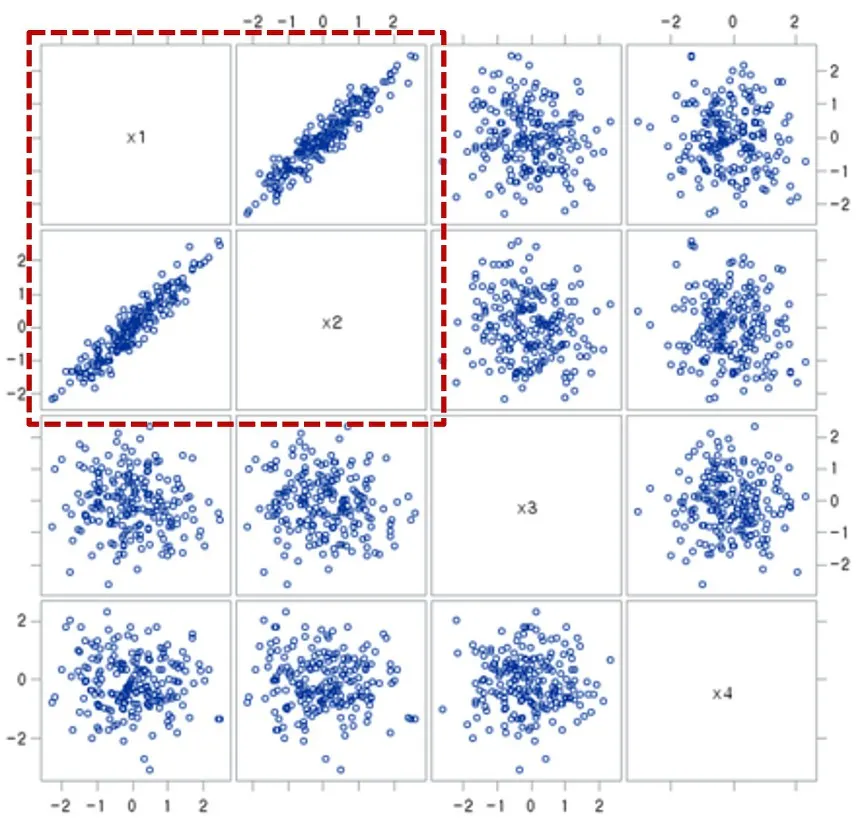
Scatter plot(산점도 그래프)
2.
Heatmap
•
•
독립 변수 a와 b가 서로 상관 관계가 있다고 했을 때 두 변수 모두 VIF가 높음(하나만 높지 않음)
다중 공선성 해결 방법
References
1.
통계학과 사색의 공간, 다중공선선(Multicollinearity)이란?, 네이버 블로그 (link)
3.
4.
다중 공선성에 대해 알아보자!, DACON (link)
5.
귀퉁이 서재, 다중공선성(Multicollinearity)과 VIF(Variance Inflation Factors), 티스토리 (link)
6.
7.
