Search

VIF (Variance Inflation Factor, 분산팽창인자)

@Hyun Ahn @7/29/2022
독립변수 사이의 다중공선성(multicolinearity)을 평가할 때 사용되는 지표

측정 방법

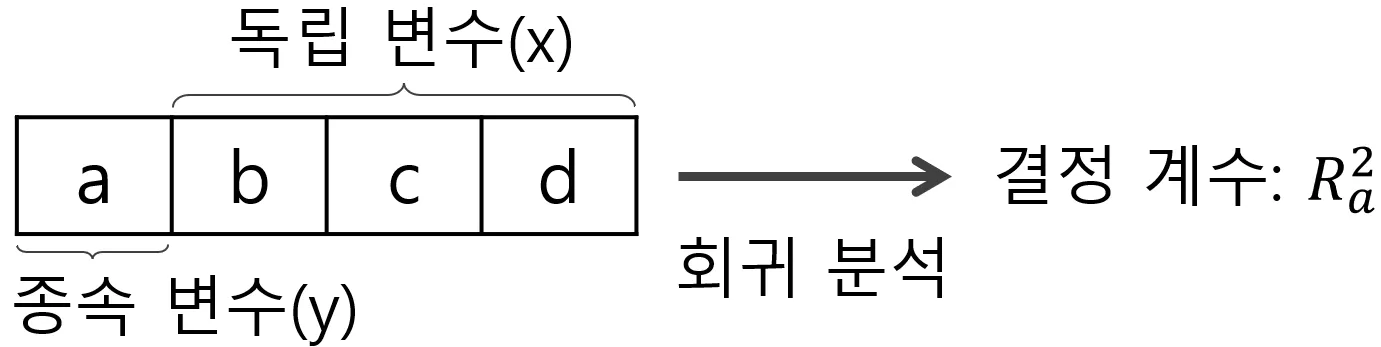
독립 변수 집합 X={a,b,c,d}X={\{a,b,c,d\}} 가 주어질 때, 특정 변수 ii의 VIF 값은 변수 ii를 종속 변수로 하고, 나머지 변수들을 독립 변수로 해서 회귀 분석을 수행
•
예: i=ai=a
•
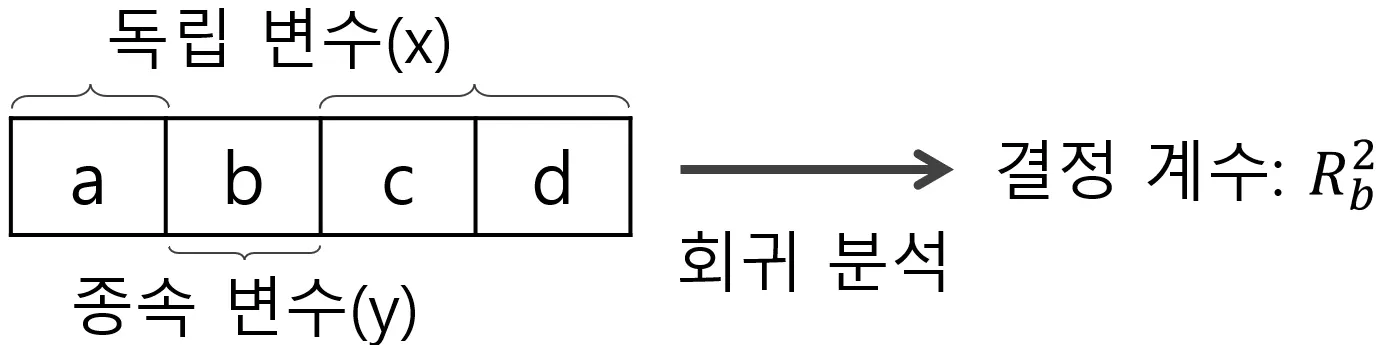
예: i=bi=b
회귀 분석을 통해 각 변수 별 결정계수들(Ra2,Rb2,Rc2,Rd2)(R_{a}^2,R_{b}^2,R_{c}^2,R_{d}^2)이 계산됨
최종적으로 변수 별 VIF 값은 다음 수식과 같음
VIF(i)=11−Ri2VIF(i)=\frac{1}{1-R_{i}^2}
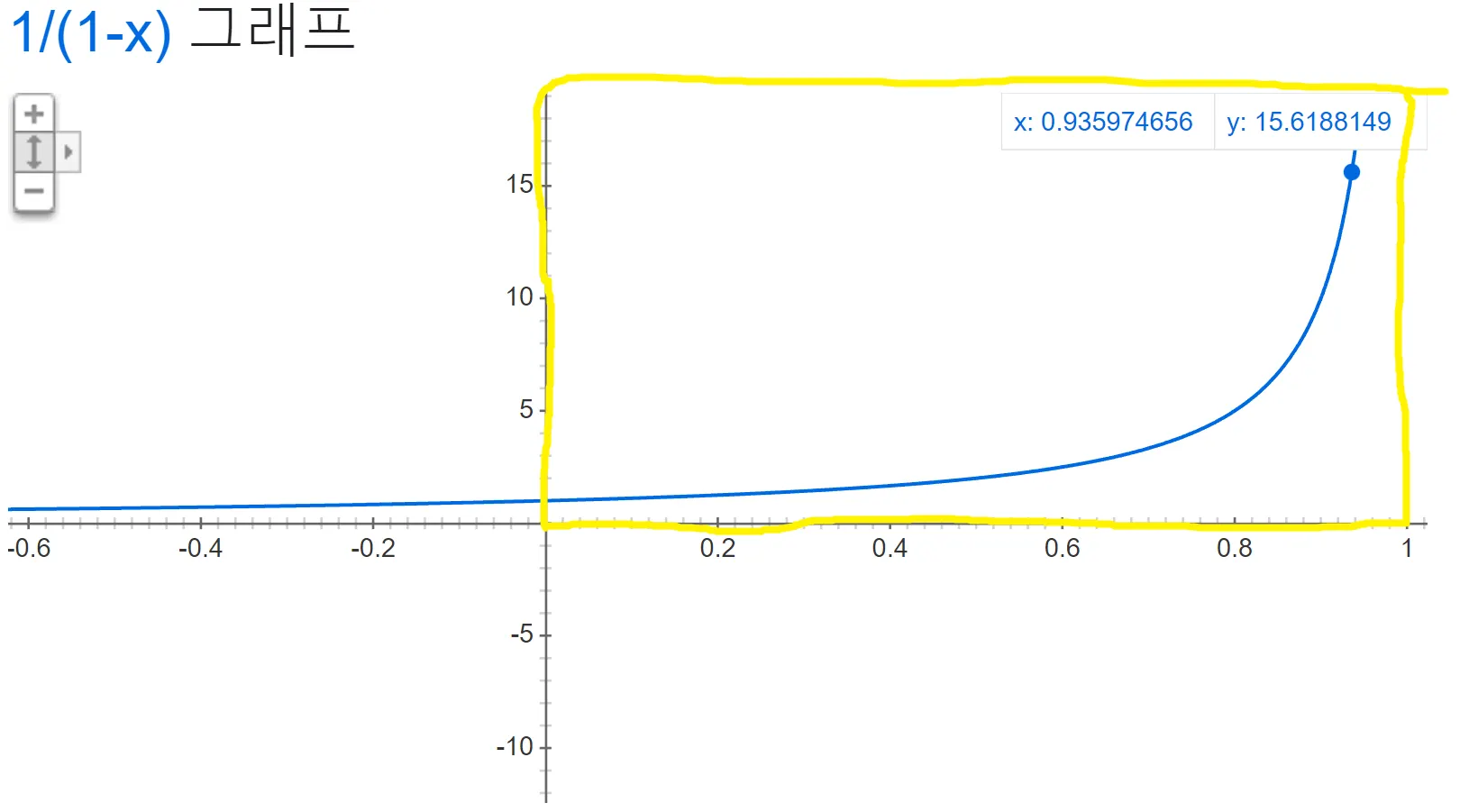
결정계수의 값 범위는 일반적으로 0≤R2≤10\leq R^2 \leq 1 이며, VIF 함수가 11−x\frac{1}{1-x} 꼴을 취하고 있음. 따라서, VIF 값은 결정계수가 작을수록 1에 근접, lim⁡Ri2→0VIF(i)=1\lim_{R_{i}^2\rightarrow 0} VIF(i)=1 . 반대로 결정계수가 클수록 무한대로 발산하는 특징을 가짐, lim⁡Ri2→1VIF(i)=∞\lim_{R_{i}^2\rightarrow 1} VIF(i)=\infty.
VIF 값의 함수적 특징
계산된 VIF(i)VIF(i)가 10 이상이면, 종속 변수 ii가 유의미한 다중공선성을 가지고 있다고 판단하며, 다른 독립 변수들에 의해 이미 충분히 설명되기 때문에 변수 제거가 고려됨

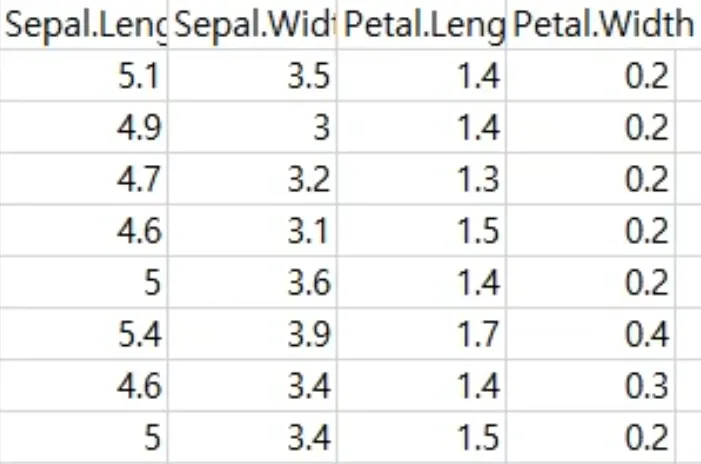
예제: Iris 데이터셋

붓꽃(iris) 종류를 예측하는 분류 모형을 만들기 위해 제공된 4개의 독립 변수들의 VIF를 계산 (출처: Jeehyoung Kim)
변수명
설명
데이터 타입
Species
붓꽃의 종 (대상 변수) (setosa, versicolor, virginica)
명목형
Sepal.Length
꽃받침의 길이
연속형
Sepal.Width
꽃받침의 너비
연속형
Petal.Length
꽃잎의 길이
연속형
Petal.Width
꽃잎의 너비
연속형
Iris 데이터셋 일부 (출처: Jeehyoung Kim)
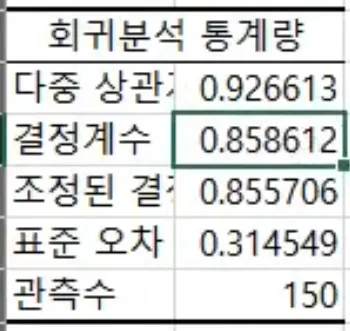
변수 Sepal.Length 의 VIF 값: Sepal.Length 를 종속 변수로, 나머지 변수들을 독립 변수로 구성해서 회귀 분석을 수행하여 얻어진 결정계수를 이용하여 계산
Sepal.Length 변수의 회귀분석 결과. VIF 계산에 필요한 결정계수를 포함한다.
•
VIF(Sepal.Length)=11−RSepal.Length2=11−0.858612=10.141388=7.072736VIF(Sepal.Length)=\frac{1}{1-R^2_{Sepal.Length}}=\frac{1}{1-0.858612}=\frac{1}{0.141388}=7.072736
나머지 변수들의 VIF 값 또한 동일한 방식으로 측정함
•
VIF(Sepal.Width)=11−RSepal.Width2=11−0.524007=10.475993=2.100871VIF(Sepal.Width)=\frac{1}{1-R^2_{Sepal.Width}}=\frac{1}{1-0.524007}=\frac{1}{0.475993}=2.100871
•
VIF(Petal.Length)=11−RPetal.Length2=11−0.968012=10.031988=31.261723VIF(Petal.Length)=\frac{1}{1-R^2_{Petal.Length}}=\frac{1}{1-0.968012}=\frac{1}{0.031988}=31.261723
•
VIF(Petal.Width)=11−RPetal.Width2=11−0.93785=10.06215=16.090105VIF(Petal.Width)=\frac{1}{1-R^2_{Petal.Width}}=\frac{1}{1-0.93785}=\frac{1}{0.06215}=16.090105
결론적으로 변수 Petal.Length와 Petal.Width의 VIF 값이 10을 넘으므로, 다중공선성이 높은 것으로 해석됨
VIF 값이 높은 변수들을 제거하는 방법 외에도 다중공선성을 해결하는 방법은 여러가지가 존재함
•
정규화 회귀분석: Ridge/Lasso regression
•
주성분회귀(PCR: Principle Component Regression) 또는 부분최소제곱회귀(PLS: Partial Least Square)
•
Random Forest, Artificial Neural Networks, SVR(Support Vector Regression) 등
•
학습 표본 크기 증가

참고 문헌

Made with