R-squared (결정계수)

@Hyun Ahn 2022-06-15

: 평균과 회귀선의 데이터 변동(variation)을 비교하여 모델의 적합도를 평가하는 지표

R-squared 의 직관적 이해

•

데이터의 변동은 평균(xˉ)(\bar{x})(xˉ)과 데이터(x)(x)(x)의 차이를 제곱한 값들의 총합

var(mean)=sum(x-\bar{x})^2

•

반면,  모델의 변동은 모델의 회귀선이 예측한 값(x^)(\hat{x})(x^)과 데이터(x)(x)(x)의 차이를 제곱한 값들의 총합

var(line)=sum(x-\hat{x})^2

여기서 떠올릴 수 있는 질문:

만약 회귀선이 평균보다 데이터를 잘 설명한다고 하면, 그 정도를 어떻게 수치로 표현할 수 있을까?

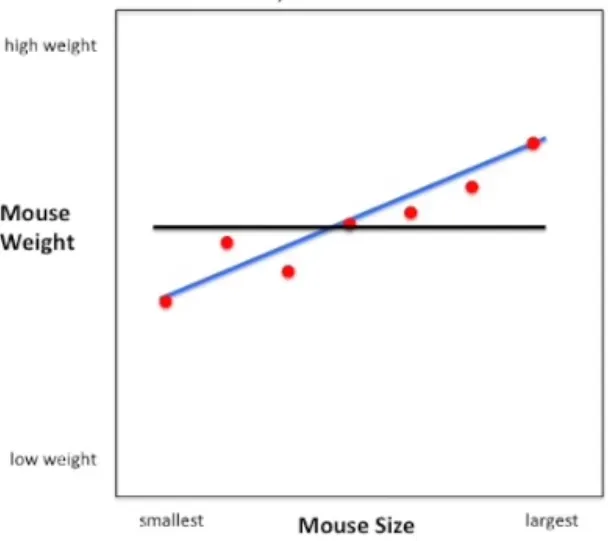
쥐의 크기(x축)와 몸무게(y축)과의 관계를 모델링한 회귀선과 평균선 (출처: [2])

R-Squared 는 평균을 기준으로 한 데이터 변동과 모델의 회귀선을 기준으로 한 데이터 변동을 비교하여 모델의 적합도를 측정하는 방법

R^2=\frac{var(mean)-var(line)}{var(mean)}

만약, 합리적인 모델링을 통해 데이터를 잘 설명하는 회귀선을 만들 경우,

var(line)

은 단순히 평균과의 차이를 기준으로 계산되는

var(mean)

보다 작으므로, 일반적으로 R-Squared 는

0\leq R^2 \leq 1

범위의 값을 갖게 됨

만약 R-Squared 값이 0.8 인 경우, 이는 모델의 회귀선의 변동이 평균의 변동과 대비하여 80% 적다는 의미를 가지므로, 해석이 간편하다는 장점이 있음

일반적인 R-squared 수식

•

Total Sum of Squares(SStot)(SS_{tot})(SStot​): 관측 값(yi)(y_i)(yi​)과 관측 값 평균(yˉ)(\bar{y})(yˉ​)과의 차이를 제곱한 값들의 총합 = 데이터 변동 = var(mean)var(mean)var(mean)

SS_{tot}=\sum_{i=1}^{n}({y_{i}-\bar{y}})^2

•

Residual Sum of Squares(SSres)(SS_{res})(SSres​): 관측 값(yi)(y_i)(yi​)과 모델의 예측 값(yi^)(\hat{y_i})(yi​^​)과의 차이를 제곱한 값들의 총합 = 모델의 오차 = var(line)var(line)var(line)

SS_{res}=\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}

R^2=1-\frac{SS_{res}}{SS_{tot}}