.png&blockId=04a8d577-ace8-4bac-bec8-3da8a3f63bbd)
@Jinyeop Kang, 2022-08-01
1. 변수 정규화
: 아무리 좋은 데이터를 갖고 있어도 모델에 학습시키기 위해서는 스케일링(Scailing)을 해줘야 한다.
정규화를 왜 해주어야 하는가?
: 머신 러닝 모델은 데이터가 가진 피쳐(feature)를 가지고 학습한다. 이 때, 모델이 받아들이는 데이터의 크기가 고르지 않다면 모델이 데이터를 이상하게 해석할 우려가 있다. 따라서 모든 데이터가 같은 정도의 스케일(중요도)로 반영되도록 해주는 것이 정규화의 목표이다. 즉, 정규화는 머신 러닝 모델에 주입 되는 데이터들을 균일하게 만드는 최고의 방법이라고 할 수 있다.
Min-Max Normalization (최소-최대 정규화)
: 모델에 투입될 모든 데이터 중에서 가장 작은 값을 0, 가장 큰 값을 1로 두고, 나머지 값들은 비율을 맞춰서 모두 0과 1 사이의 값으로 스케일링 해주는 것.
•
If the value of X is Min-Max Normalized, it will be
•
이상치(outlier)에 매우 취약하다.
◦
한 데이터만 다른 데이터들과 달라도 고른 형태의 데이터 분포를 기대하기 어렵다.
Z-Score Normalization (Z-점수 정규화)
: 표준화 작업이라고도 부른다.
•
X(원점수)라는 값을 Z(Z-점수)로 정규화 함으로써 평균이 0, 표준편차가 1인 표준 정규 분포를 얻을 수 있다.
•
어떤 데이터가 표준 정규 분포(가우시안 분포)에 해당하도록 값을 바꿔준다.
•
값이 넓게 퍼져 있다면(데이터의 표준 편차가 크면), 정규화 되는 값이 0에 가까워진다.
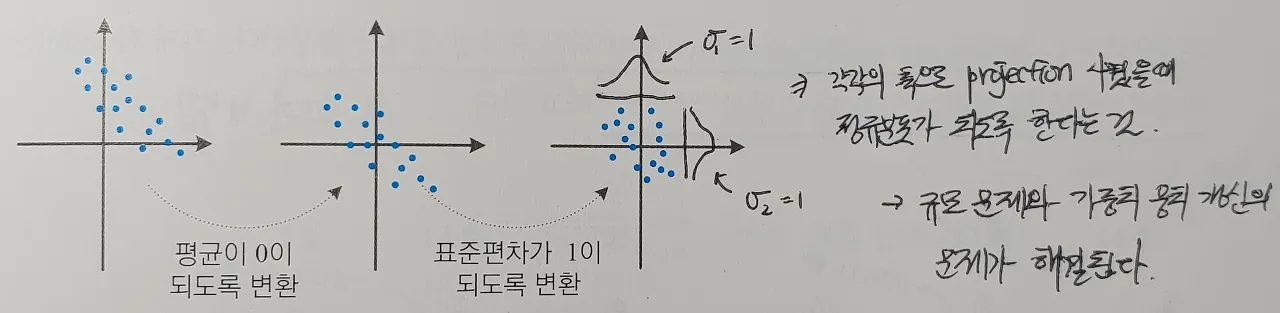
위 그림은 불균형한 데이터 분포를 평균이 0, 표준편차가 1이 되도록 변환한 것을 나타낸다. (정규화) 즉, 각각의 축으로 투영(projection)시켰을 때 정규분포가 되도록 한다는 것이다.
2. 변수 제거
: VIF(Variance Inflation Factors) 기준 10 이상의 변수들을 제거하는 방법이다.
•
다중공선성을 가진 변수는 혼자 존재하지 않는다.
◦
만약 a, b, c, d의 변수를 가진 회귀 분석을 수행할 떄, a 변수 혼자 다중공선성을 가질 수는 없다.
•
해결 방법
1.
두 변수 중 하나를 제거한다.
2.
제거 시 유지되는 변수를 제거한다.
