7️⃣

시계열의 상태공간 모델

상태공간 모델 : 통계 모델과 유사하나 ‘실세계’에서 얻은 동기에 영향을 받는 모델. 참 상태(true state)를 직접 측정할 수 없으며 측정된 것으로부터 추정하는 것만 가능함.

•

추정 시 측정 오류 고려

•

사전 지식이나 믿음을 추정에 주입

내부 역동성 및 외부 압력에 의해 시간에 따라 변함.

Example

•

상대 운전자가 공격적으로 차선 변경을 시도할 때, 차선 진로 변경 추측 

→ 음주운전자로 판단될 경우 경찰에 신고

→ 휴대폰을 보느라 집중력을 잃었던 것이면 신경쓰지 않음

•

우주선으로 발사된 로켓. 

→뉴턴의 법칙을 활용한 시스템 역동성 및 시간에 따른 움직임의 변화 규칙 생성

지상풍이나 태양풍처럼 알 수 없는 노이즈에서도 과정을 만들어내야 함.

→ 이를 위해, 상태공간이라는 개념이 개발되었으며, 당시에는 시스템의 다른 불확실성으로부터 측정 오차를 명확하게 하려함.

일반적으로 상태 공간의 방법

•

선형 가우스 모델에 적용된 칼만 필터

•

은닉 마르코프 모형

•

베이즈 구조적 시계열

7.1 상태공간 모델의 장단점

•

상태공간 모델은 확률적이거나 결정론적인 응용 단계 모두에서 사용 가능하며, 연속적이거나 이산적으로 샘플링된 데이터에 적용 가능함.

→ 상태공간 모델의 활용도가 매우 높고, 상당한 유연성을 가짐.

상태공간 모델의 장단점은 상태공간이 지닌 유연성에서 발생함.

•

상태공간 모델의 장점

◦

노이즈가 존재하는 데이터 자체보다 노이즈한 데이터의 생성 과정과 상태를 모델링하는 데 강점이 있음.

◦

일반적으로 이미 익숙한 시스템의 역동성을 자세히 파악하는 데 유용함.

→ 시간에 따른 상관계수 및 파라미터의 변화를 허용함.(시간에 따라 변화하는 행동을 허용함.)

→ 상태공간 모델 사용 시 정상성 조건을 부과하지 않음.

•

상태공간 모델의 단점

◦

상태공간 모델은 매우 유연하여 수많은 파라미터의 설정이 가능함. 따라서 수많은 종류의 상태공간 모델이 존재할 수 있음.

◦

수많은 파라미터로 구성된 상태공간 모델은 계산적으로 매우 부담스러움. 또한, 많은 파라미터로 구성된 일부 상태공간 모델의 경우 과적합에 취약함.(특히, 데이터가 적은 경우 과적합 발생 가능성이 높아짐.)

7.2 칼만 필터

칼만 필터의 역할 : 시계열로부터 새로운 정보를 결함하는 데 활용되며 과거에 알려진 내부 상태 추정 정보를 지능적으로 결함함.

칼만 필터의 장점 : 계산이 비교적 간단하고, 미래 예측이나 현재를 추정하는 데 과거 데이터의 저장이 필요하지 않음.

시계열 데이터에 노이즈가 들어오더라도 제거에 좋은 역할을 하며, 지속적으로 변화하는 시스템에 이상적임.

•

Kalman Filter

x_t = F\times x_{t-1} + B \times u_t + w_t

y_t = A \times x_t + v_t

◦

F×xt−1F\times x_{t-1}F×xt−1​ : 이전 시간 단계의 상태 항

◦

B×utB\times u_tB×ut​ : 외부압력에 대한 항

◦

wtw_twt​ : 확률적 항(시스템 잡음)

◦

vtv_tvt​ : 측정 잡음

ex.

x_t

는 차량의 실제 위치,

y_t

는 검출로 측정된 위치일 때,

v_t

는 검출기의 측정 오차를 의미함.

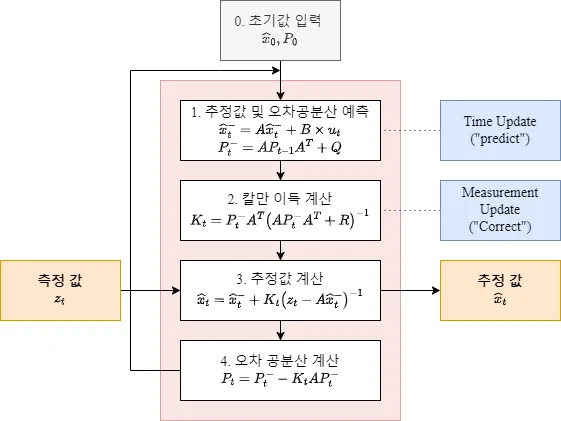
칼만 필터의 계산식

•

계산 식에서는 wt,vtw_t, v_twt​,vt​을 제거한 나머지 항에 대한 연산을 수행함.

•

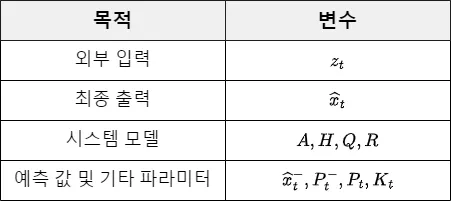
칼만필터의 목적과 변수

◦

칼만 필터의 연산 값은 ‘예측 값 및 기타 파라미터’이며,  ‘시스템 모델’은 정해져 있는 값(데이터)임.

•

시간 ttt에서 새로운 정보가 주어졌을 때, 추정을 갱신하는 방법

\hat x_t = K_t \times y_t + (1-K_t) \times \hat x_{t-1}

•

위의 식에서는 KtK_tKt​가 새로운 정보(yty_tyt​)와 과거의 정보(x^t−1\hat x_{t-1}x^t−1​) 사이의 추정에 대한 균형을 맞추는 데 활용됨을 알 수 있음.

•

동적 과정 세분화(참고)

•

상태의 공분산 추정 값은 PtP_tPt​로 표현됨. (상태 정보는 일반적으로, 다변량이기 때문에 행렬이 됨.)

•

측정 오차의 공분산 행렬, 대각행렬 : RRR

◦

vtv_tvt​에 대한 공분산이 됨.

•

시스템 오차에 대한 공분산 행렬, 대각행렬 : QQQ

◦

wtw_twt​에 대한 공분산이 됨.

◦

RRR과 다르게 명확하지 않으므로 모델링 시 조정이 필요함.

•

시간 0에서 이미 알고 있는  xxx와 추정된 공분산 값인 PPP로 구성된 과정으로 시작함. 이후, 시간 0에서 시간이 뒤로 지연되며 예측과 갱신을 반복함.

•

먼저, 예측 단계가 발생한 다음 갱신 및 필터링 단계가 실행됨.

◦

예측

\hat x^-_t = F \times \hat x_{t-1} + B \times u_t

▪

FFF는 운동방정식에 의한 거리의 변화량을 표현하는 등속 운동의 식임. → 이전(xt−1x_{t-1}xt−1​)에서 FFF를 곱하면 현재 추정 값이 됨. 다만, 가속도에 따른 행렬 형태를 식에 추가할 필요가 있음.

증명(FFF)

▪

BBB는 control matrix를 의미하며, utu_tut​는 control vector를 의미함.

증명(B×utB\times u_tB×ut​)

P^-_t = F \times P_{t-1} \times F^T + Q

◦

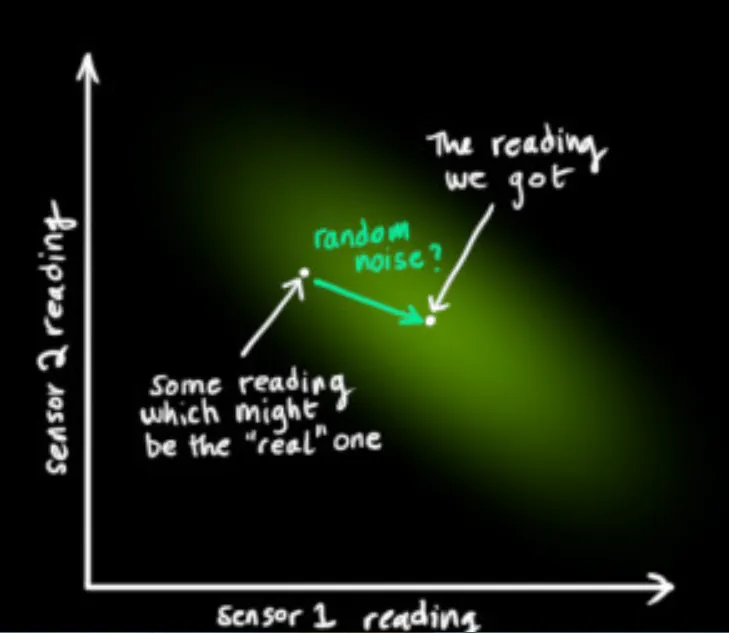
아무리 완벽한 측정기여도 ‘실세계’인 경우 noise가 존재함.

◦

noise QQQ가 추가된 prediction 영역에 대한 추정 오차 분산 값 → 측정한 결과를 항상 신뢰할 수 없기 때문에 노이즈가 포함된. 센서 값의 범위로 변환함.

새로운 불확실성인

P_t

는 이전의 불확실성인

P_{t-1}

로부터 도출된 시스템 내부의 불확실성임.

Q

는 시스템 외부에 존재하는 불확실성을 추가한 경우를 의미함.

◦

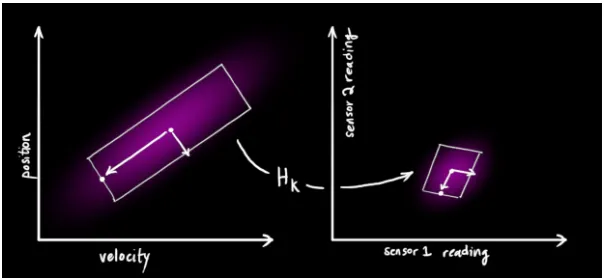
필터링

\hat x_t = \hat x^-_t + K_t \times (y_t - A \times \hat x_t)

▪

예측 값과 센서 값에는 unit 및 scale의 차이가 있을 수 있어 변환할 필요가 있음. AAA는 추정된 예측 값을 센서값으로 변환하기 위한 행렬임. → 이를 ‘상태공간방정식’이라고 부름.

▪

yty_tyt​는 측정값을 의미함.

P_t = (I-K_t \times A) \times P^-_t

◦

KtK_tKt​는 칼만이득으로 다음을 뜻함.

▪

RRR도 noise임. (QQQ는 사용자에 의해 임의로 결정된 적절한 noise를 의미하며, RRR은 측정기에서 발생하는 일반적인 noise를 의미함.)

K_t = P^-_t \times A^T \times (A \times P^-_t \times A^T \times R)^{-1}

◦

결과론적으로, A,Q,H,RA, Q, H, RA,Q,H,R은 칼만 필터와 상관없이 정해진 값이며, xxx와 PPP에 대한 값이 가장 중요함.

•

칼만 필터 계산 과정 (참고)

◦

쉽게 이해하기(참고)

7.2.2 코드로 표현한 칼만 필터

•

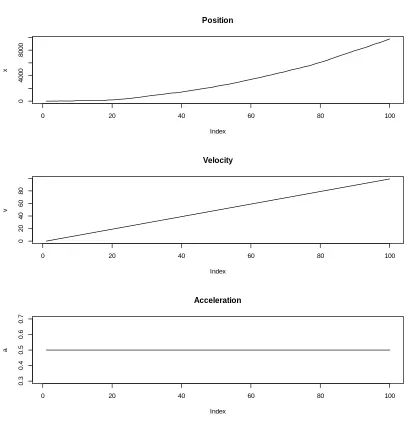
물체의 위치를 물체의 속도와 가속도에 대한 함수로 보는 뉴턴 운동 법칙에 따라 시계열을 생성함.

◦

물체의 움직임은 계속성을 가지며, 측정은 이산적으로 분리됨을 가정함.

◦

가속도에 대한 계열을 정하고, 위치와 속도는 0에서 시작함.

◦

물리적으로 비현실적이나 각 시간 단계의 시작점에서 순간 가속도가 변하고 다시 변하기 전까지 지속적인 값을 가짐을 상정함.

## 로켓은 시간 단계를 100번 거칩니다.
ts. length <- 100
## 가속도가 움직임을 주도합니다.
a <- rep(.05, ts.length)

## 위치와 속도는 0에서 시작합니다.
x <- rep(0, ts.length)
v <- rep(0, ts.length)
for (ts in 2:ts.length) {
	x[ts] <- v[ts-1] * 2 + x[ts-1] + 1/2 * a[ts-1] ^ 2
	x[ts] <- x[ts] + rnorm(1, sd = 20) ## 확률적 요소
	v[ts] <- v[ts-1] + 2 * a[ts-1]
}
R
복사

◦

‘a’라는 변수에 0.05를 100번 반복한 벡터를 할당함. → 가속도는 모든시간 단계에서 일정한 0.05를 가짐.

◦

‘x’와 ‘v’에 각각 0을 할당함. → 초기 위치와 속도를 0으로 만듦.

◦

for 반복문은 2부터 100까지 반복되며, 로켓의 위치와 속도가 시간에 따라 변화하는 과정을 시뮬레이션 함.

•

로켓의 움직임 그래프 그려보기

par(mfrow = c(3,1))
plot(x, main = "Position", type = 'l')
plot(v, main = "Velocity", type = 'l')
plot(a, main = "Acceleration", type = 'l')
R
복사

z <- x + rnorm(ts.length, sd = 300)
plot (x, ylim = range(c(x,z)))
lines(z)
R
복사

•

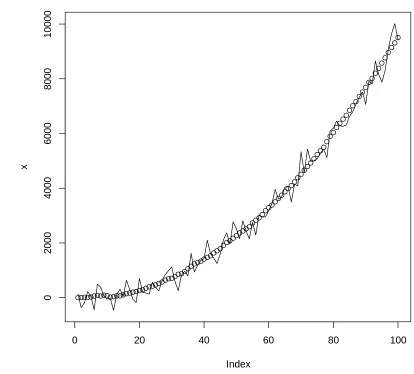
노이즈한 센서로부터 얻을 수 있는 물체의 위치

•

측정된 값이 실제 위치와 어떤 관계를 갖는지에 대한 그래프임.

•

칼만 필터 적용해보기

kalman.motion <- function(z, Q, R, A, H) {
	dimState = dim(Q)[1]
	
	xhatminus <- array(rep(0, ts.length * dimState), c(ts.length, dimState)
	xhat <- array(rep(0, ts.length * dimState), c(ts.length, dimState)
	
	Pminus <- array(rep(0, ts.length * dimState * dimState),
													c(ts.length, dimState, dimState)
	K <- array(rep(0, ts.length * dimState),
								c(ts.length, dimState)) # 칼만이득
	# 초기 추측 = 모든 지표는 0으로 시작함.
	xhat[1, ] <- rep(0, dimState)
	P[1, , ] <- diag(dimState)
	
	# 시간 갱신
	for (k in 2:ts.length) {
		# 예측
		xhatminus[k, ] <- A %*% matrix(xhat[k-1, ]) # %*% 행렬 곱셈 연산자
		Pminus[k, , ] <- A %*% P[k-1, , ] %*% t(A) + Q
		
		# 필터링
		K[k, ] <- Pminus[k, , ] %*% H %*%
							solve(t(H) %*% Pminus[k, , ] %*% H + R )
		xhat[k, ] <- xhatminus[k, ] + K[k, ] %*%
											(z[k] - t(H) %*% xhatminus[k, ])
		P[k, , ] <- (diag(dimState)-K[k, ] %*% t(H)) %*% Pminus[k, , ]
	}
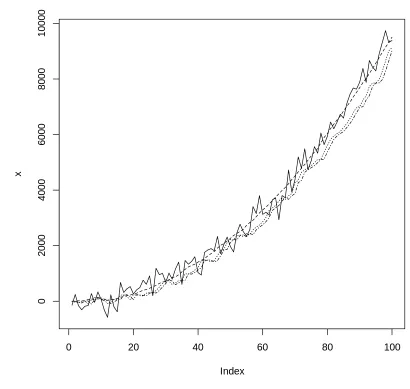
	## 예측과 평활화된 값 모두 반영
	return(list(xhat = xhat, xhatminus = xhatminus))
}
R
복사

•

이 함수는 로켓의 위치만을 측정 가능하게 만들어줌. (속도와 가속도는 포함되지 않음.

## 노이즈 파라미터
R <- 10^2
Q <- 10

## 동적 파라미터
A <- matrix(1) # 사전 x가 나중 x에 얼마나 영향을 미치는 지
H <- matrix(1) # 상태를 측정으로 변환

## 칼만 필터 방법을 데이터를 넣고 돌림.
xhat <- kalman.motion(z, diag(1) * Q, R, A, H)[1]]
R
복사

7.3 은닉 마르코프 모형

7.3.1 모델의 동작방식

•

모델 가정

◦

Hidden Markov Model(HMM)은 직접적으로 관측이 불가능한 상태를 가진 시스템을 상정

◦

미래 사건의 확률이 시스템의 현재 상태만으로도 충분히 계산될 수 있음 

•

Markov과정

◦

두 상태 모두 다른 시간 단계에서 통계적으로 다른 상태로 바
뀌는 것보다는 현 상태를 유지할 가능성이 높다고 가정

◦

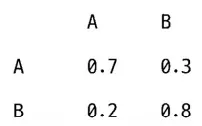
현재 시스템 상태 A，（1 , 0）일때（상태 B는（0 , 1））. 이때 시스템이 상
태 A를 유지할 확률은 0 . 7이며，상태 B로 바뀔 확률은 0 . 3

•

은닉 마르코프 모형(hidden Markov model)

◦

관측으로부터 시스템의 상태를 직접적으로 추론할 수 없고, 관측은 시스템의 상태에 대한 단
서를 제공（그림 7-4）

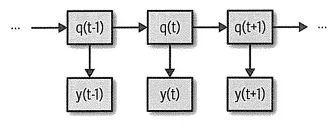
그림 7-4 HMM에 대한 과정으로 특정 시간에서 시스템의 실제 상태를 x(t)로 표현합니다. 또 특정 시간에서 관측 가능한 데이터는y(t)로 표현합니다. y(t) 입장에서는 오로지 x(t)만 고려. 즉 x(t)를 이미 알고 있다면 x{t-1)은 y(t) 예측에 추가 정보를 제공하지 않는 것입니다. 마찬가지로 y(t十1)의 예측에는 x(t)의 영향만 있을 뿐，x(t~ 1)로 부터는 어떠한 추가 정보도 없습니다. 이것이 바로 마르코프가 바라보는 시스템입니다.

•

HMM의 실제 사용 사례

◦

금융시장의 체제 전환식별

◦

DNA 염기순서 정보의 분류，예측，복원

◦

ECG 데이터에 반영된 수면 단계의 인식

7.3.2 모델을 적합 시키는 방법

•

시스템 구성 가정

◦

x(t)에서 x(t+1)로 전환될 확률. 행렬로 표시, 크기는 상태의 개수에 따라 다름

◦

x(t)가 주어졌을 때 관측y(t)가 나타날 확률 emission probability

◦

시스템의 초기 상태

•

모델 적합화 단계

◦

가능한 각 은닉상태에 대한 개별 방출 확률과 각 은닉상태 간의 전환 확률을 추정.(바움-웰치 알고리듬)

◦

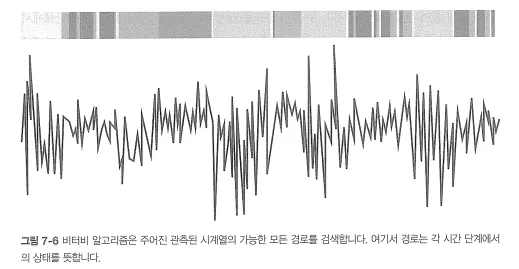
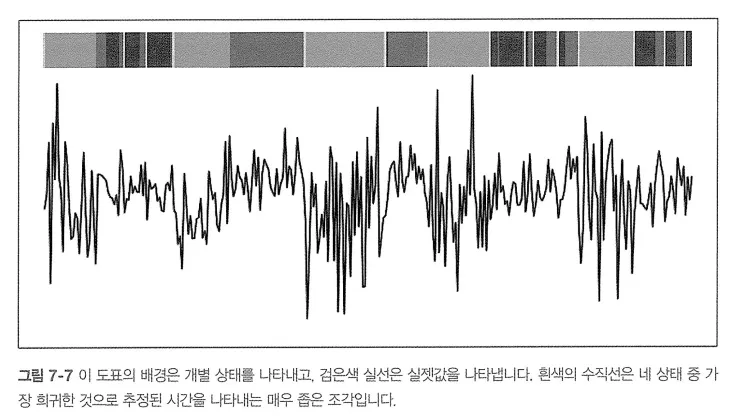
전체 관측에서 각 시간 단계별 가장 가능성이 높은 은닉 상돼를 식별.  (비터비 알고리즘)

•

바움-웰치 알고리듬(Baum-Welch Algorithm)

◦

우도 함수(Likelihood Function)의 정의

▪

 우도 함수는 주로 매개변수 추정, 특히 최대우도추정법(Maximum Likelihood Estimation, MLE)에서 사용. 이 함수는 관찰된 데이터가 주어졌을 때, 가능한 매개변수 값들의 우도를 나타내며, 이를 통해 가장 데이터를 잘 설명하는 매개변수 값을 찾음.

◦

우도 함수의 적용

▪

두 개의 분포를 상정하는 무작위 사건 및 각 시간 단계에서 특정 상태일 확률을 결정（예: 시간 단계 에서 상태 A나 B가 될 확률）

▪

 각 시간 단계에 추정 상태를 할당하면，그 추정 상태로 방출 확률을 재추정

▪

 과정을 반복하여 궤적의 추적 향상 을 위해 새롭게 갱신된 방출 확률변수를 사용하여

미분, 수치적 최적화 기법 등을 사용하여 최대우도 추정값 도출

◦

비터비 알고리즘

▪

HMM 과정의 파라미터가 관측 가능한 측정값으로 구성된 시계열을 구성하게 하는 가장 가능성 높은 상태들의 계열 추정

▪

동적 프로그래밍 알고리즘. 즉 특정 해결책에 도달하기 위해 부분적인 해결책을 만들고 저장하여，적합 범위를 완전하면서도 효율적으로 탐색.

동적 프로그래밍

7.3.3 코드로 보는 HMM의 적합 과정

•

depmixS4 패키지로 작업. 

◦

코드를 시용해 적절한 시계열을 만듬

◦

상기 코드는 매수세, 약세, 중립, 패닉이라는 네 가지 모드의 주식시장에서 영감을 받은 예제. 각 상태의 방출 확률 분포를 설명하는 변수(특정 상태에서 측정된 기대 값을 나타내는  mu 및 -Sd 변수)와 같이 상태가 지속될 일수는 무작위로 선택

◦

샘플이 포괄하는 날 중 몇 일이 상태 추적에 시용하는 변수인 true.mean에 해당하는지 확인해 생성된 시계열의 모양과 각 상태의 빈도를 파악

◦

모델은 두 단계로 적합

▪

 우선 예상 분포, 상태 개수, 적합에 사우될 입력 데이터 등이 depmix() 함수로 지정. 다음 fit 함수를 통해 모델이 적합. 이때 fit 함수에는 모델 사용에 대한 내용이 전달. 

▪

마지막으로 posterior() 함수를 사우하여 적합된 모델로부터 상태 레이블에 대한 사후분포를 생성.

▪

상기 코드에서는 관측데이터로 returns 벡터를 제공하여 hmm.model을 생성. 상태의 개수(4)를 지정, family 파라미터를 통해 방출 확률이 가우스 분포를 따른다는 것 을 지정. 그다음 fit() 함수로 모델을 적합, posterior() 함수로 사후 획률을 계산. 사후 획률은 적합 과정에서 결정된 모델의 피라미터에로 특정 시간에서의 특정 상태에 대한 확률을 제공.

•

다음과 같이 측정된 값으로 상태를 시각화 

•

HMM은 다양한 종류의 데이터를 분석하는 데 적합. 현재 금융시장이 성장기인지, 불황 기인지를 모델링하고 세포 내의 단백질 폴딩이 어느 단계에 있는지 결정하며 (딥러닝이 도래 하기 전) 사람의 움직임을 설명하는 데 시용. 이러한 모델은 예측하기 보다 시스템의 역동성을 이해하는 데 더 지주 우통하게 사용됩니다. 

•

HMM을 시용할 때 다음과 같은 몇 가지 추론 작업에 직면.

◦

괸측의 계열을 생성하는 상태들의 가장 가능성 있는 설명을 결정

◦

관측의 계열, 상태에 대한 설명, 각 상태의 방출과 전환 획률을 통해 가장 기능성이 높은 상태의 연속적인 순서를 결정.

◦

필터링과 평활화입니다. 필터링은 가장 최근의 관측이 주어졌을 때 가장 최근의 시간 단 계에서의 은닉 상태를 추정. 평활회는 특정 시간 단계의 이전, 현재, 이후에 대한 관측을 토대로 해당 시간 단계의 은닉 상태에 대한 가장 가능성 있 는 분포를 결정.

7.4 베이즈 구조적 시계열(BSTS)

•

베이즈 구조적 시계열 모델(BSTS) 

◦

베이지안 통계학과 구조적 시계열 모델을 결합한 형태의 시계열 분석 기법 

◦

특징 : 트렌드, 계절성, 회귀 성분 등 다양한 구조적 구성 요소 포함 

•

베이지안 접근법

◦

베이지안 통계 기본 개념 : 사전확률prior probability과 사후확률posterior probability를 사용하여 불확실성을 정량화 함

베이지안 통계

•

구조적 시계열 모델

◦

시계열 데이터를 구성 요소로 분해, 각 요소 모델링, 결합하여 전체 시계열을 설명하는 방법 

◦

추세, 계절성, 순환성, 잔차, 회귀 등의 구성요소로 분해

◦

시간에 따라 증가하거나 감소하는 장기적인 경향

◦

선형 추세, 다항 추세, 로컬 레벨 추세 

◦

해석 용이성 : 각 구성 요소의 의미를 쉽게 해석할 수 있어, 데이터의 구조를 명확히 이해할 수 있음

◦

유연성 : 다양한 시계열 데이터에 적용할 수 있는 유연한 모델링 기법 

•

BSTS와 칼만 필터  공통점 

◦

상태 공간 모델 기반, 숨겨진 상태 변수를 사용하여 시계열 데이터를 모델링 함 

•

BSTS와 선형 가우스 모델의 차이점

◦

모델링 접근법

▪

선형 가우스 모델 : 시스템의 선형성과 가우스 잡음을 가정 

▪

BSTS : 복잡한 모델링을 위한 다양한 구조적 요소를 베이즈적으로 통합 

◦

추론 방법 

▪

선형 가우스 모델 : 칼만 필터를 통한 점 추정 

▪

BSTS : MCMC(Markov Chain Monte Carlo)를 통한 확률적 추정 

•

BSTS 의 장점 

◦

유연성 : 다양한 구조적 요소를 포함하여 복잡한 시스템을 모델링 

◦

베이즈 추론 : 모델 파라미터와 상태에 대한 불확실성을 자연스럽게 처리 

◦

적합 기법 : 사전 분포와 데이터로부터 모델 파라미터를 추정 

•

구조 설계 및 파라미터 추정 

◦

구조 설계 : 모델에 포함할 트렌드, 계절성, 회귀 요소 등을 정의 

◦

파라미터 추정 : 베이즈 추론을 통해 사전 분포와 데이터로부터 모델 파라미터를 추정 

•

예시 

◦

경제 지표 모델 : GDP 성장률과 실업률을 포함한 경제 지표 모델링 

◦

기상 모델 : 온도, 압력, 습도 등의 기상 데이터를 통한 예측 모델링 

•

BSTS 모델 적합 과정 

◦

사전 확률 및 구조적 모델 정의 

▪

구조적 모델 정의 

•

트렌드, 계절성, 회귀 요소 포함 

•

사전 확률(prior probabilities) 설정 

▪

목적 : 시스템에 대한 이미 알려진 사실이나 가설 반영 

사전확률과 사후 확률 

◦

칼만 필터 적용 

▪

상태 추정 갱신 

•

관측된 데이터를 바탕으로 상태 추정 

•

칼만 필터를 사용하여 현재 상태를 업데이트 

▪

목적 : 실시간으로 상태 변수의 최적 추정치 확보 

◦

스파이크앤슬랩 변수 선택 

▪

변수 선택 방법 

•

Spike and slab method를 사용 

•

중요한 변수와 중요하지 않은 변수 구분 

▪

목적 : 모델의 복잡성을 줄이고 중요한 변수 식별 

스파이크앤슬랩 메소드(Spike and Slab Method) 

◦

베이즈 모델 평균화(Bayesian Model Averaging) 

▪

결과 결합 

•

다양한 모델의 결과 결합 

•

베이즈 모델 평균화 적용 

▪

목적 : 예측의 정확도와 신뢰성 향상 

베이즈 모델 평균화(BMA) 

7.4.1 코드로 살펴보는 bsts

•

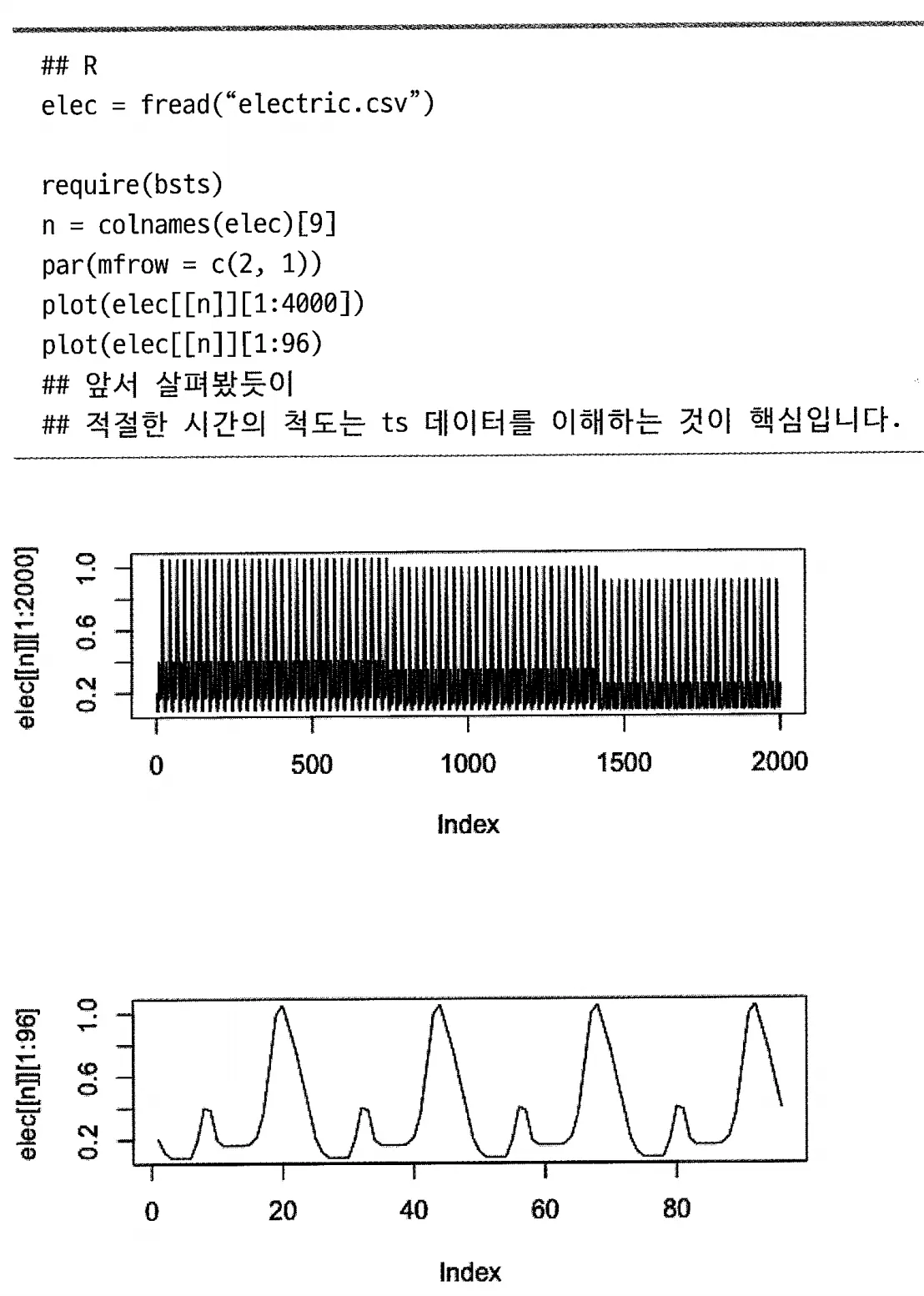
BSTS 패키지인 bsts와 OpenEL.org(http://openei.org/wiki/Main_Page)에서 취득한 개방형 데이터를 사용한 데이터 그래프 (그림 7-8) 

OpenEL.org에서 가져온 전력 소비 데이터를 사용 두개의 다른 시간 척도에서 데이터의 변화를 시각화하는 과정을 보여줌. 첫번째 플롯은 긴 시간 척도에서의 데이터를 두번째 플롯은 짧은 시간 척도에서의 데이터를 나타냄 데이터의 시간적 패턴을 이해하는데 도움이 됨

•

(그림 7-8) 상단 그래프 : 모델을 적합시켜야 하는 전체 계열 
                 하단 그래프 : 전체를 짧게 잘라낸 부분집합 
⇒일일 패턴을 분명히  보여 줄 수 있는 방법 

•

데이터는 명백한 일일 및 요일별 패턴을 보여줌 

•

이러한 패턴들은 모델링에서 계절성을 설명하는데 사용됨

•

전체 데이터를 보면 비정상적인 동작이 보임 

•

데이터의 추세를 반영해 이런 비정상 동작을 허용하는 모델을 만듬 

•

ss <- AddLocalLinearTrend(list(), ele[[n]])

◦

기본 상태 공간 리스트에 로컬 선형 추세 모델을 추가하여 데이터의 추세를 포착함 

•

ss <- AddSeasonal(ss, elec[[n]], nseasons = 24, season.duration =1) 

◦

하루동안의 24시간 주기 계절성을 상태 공간 모델에 추가하여 일일 패턴을 반영함 

•

ss <- AddSeasonal(ss, elec[[n]], nseasons = 7, season.duration = 24) 

◦

 주 단위의 7일 주기 계절성을 추가하여 요일별 패턴을 반영함 

•

지역적 선형 추세(AddLocalLinearTrend) 

◦

데이터 추세의 평균과 기울기가 모두 확률보행을 따른다고 가정

◦

모델의 계절성 요소 

▪

두 개의 인수 (계절의 개수 & 계절의 길이) 

▪

첫번째 요소는 일일 주기를 반영, 매 시간마다 하나의 계절을 가지며 각 계절은 한 시간 지속하도록 설정 

▪

두번째 요소는 주간 주기를 반영, 매 요일마다 하나의 계절을 가지며 각 계절은 24시간 지속하도록 설정 

◦

일관성의 중요성 

▪

정확한 시작 시간보다 데이터의 반복 패턴을 일관되게 반영하는 것이 더 중요함 

▪

데이터를 24시간으로 분할하는 방법은 계절성 분석에 적합함 

•

bsts 패키지의 장점 

◦

사후 확률에 대한 마르코프체인 몬테카를(MCMC)로 계산을 여러 번 수행할 수 있음 

◦

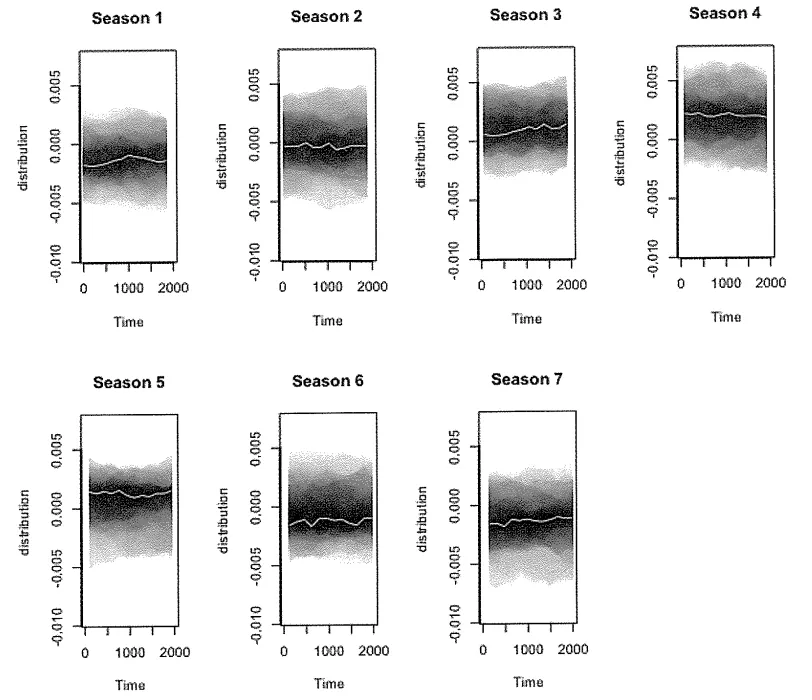
요일별 계절성 요소도 검사할 수 있음 (그림 7-9 및 7-10) 

•

(그림 7-9) 요일별 계절성은 서로 다른 요일에 따라 차이가 있다는 것을 보여줌 

•

요일별 파라미터별 분포는 요일별 추세가 시간의 흐름에 걸쳐 안정적임을 보여줌  

•

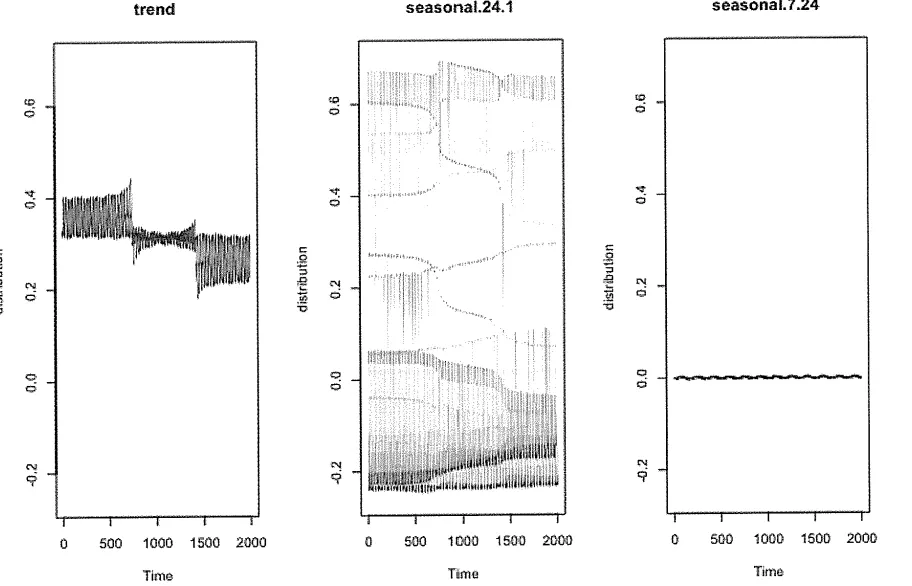
(그림 7-10) 데이터 추세, 일별, 요일별 계절성 요소의 기여도 분포 보여줌 
→ 세 요소 더하면 예측값 얻을 수 있음 

•

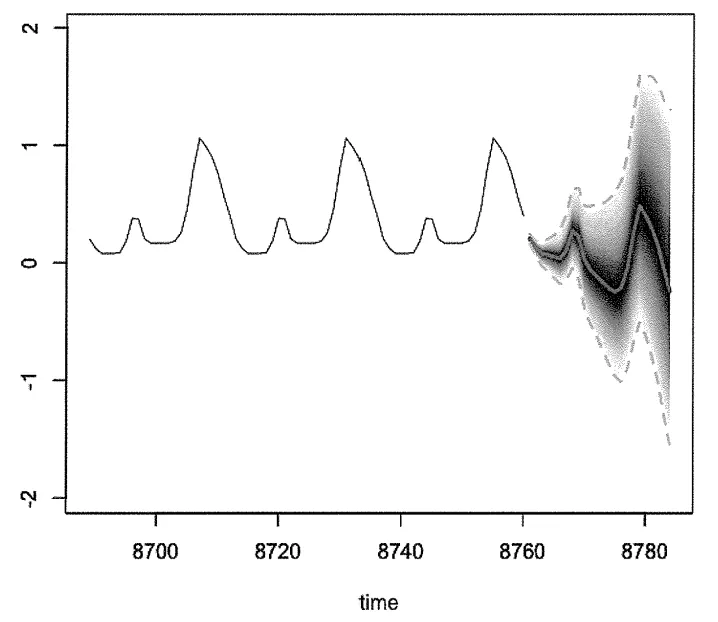
(그림 7-11) 마지막 72시간의 데이터와 예측된 24시간의 데이터의 결합 
                   미래를 예측할 수록 분포가 넓어짐 

•

BSTS 패키지의 유용한 옵션 

◦

비표준적인 사전 확률을 지정

▪

다양한 사전 확률을 모델에 주입할 수 있음 

▪

표준적인 선형 가우스 모델 외에도 비대칭 사전 확률 등 더 많은 옵션을 제공함 

◦

회귀 모델 선택에 스파이크앤슬랩 방법을 사용 

▪

스파이크앤슬랩을 통해 회귀 모델의 변수 선택 수행할 수 있음 

◦

베이즈 모델 평균화를 사용 

▪

여러 모델을 결합하여 초기 모델 선택의 불확실성을 설명할 수 있음

사전 확률 : BSTS 에서는 모든 종류의 사전 확률을 모델링에 주입할 수 있음, 칼만 필터의 표준적인 선형 가우스 모델 보다 훨씬 더 많은 옵션을 제공

변수 선택 : 스파이크 슬랩 방법을 사용하여 모델의 변수 선택을 효과적으로 수행할 수 있음

베이즈 모델 평균화 : 여러 모델은 베이즈 모델 평균화로 결합하여 초기 모델 선택과 관련된 불확실성을 설명하는데 도움됨

7.4 베이즈 구조적 시계열(BSTS)_박소연 작성중