•
베이즈 구조적 시계열 모델(BSTS)
◦
베이지안 통계학과 구조적 시계열 모델을 결합한 형태의 시계열 분석 기법
◦
특징 : 트렌드, 계절성, 회귀 성분 등 다양한 구조적 구성 요소 포함
•
베이지안 접근법
◦
베이지안 통계 기본 개념 : 사전확률prior probability과 사후확률posterior probability를 사용하여 불확실성을 정량화 함
베이지안 통계
•
구조적 시계열 모델
◦
시계열 데이터를 구성 요소로 분해, 각 요소 모델링, 결합하여 전체 시계열을 설명하는 방법
◦
추세, 계절성, 순환성, 잔차, 회귀 등의 구성요소로 분해
◦
시간에 따라 증가하거나 감소하는 장기적인 경향
◦
선형 추세, 다항 추세, 로컬 레벨 추세
◦
해석 용이성 : 각 구성 요소의 의미를 쉽게 해석할 수 있어, 데이터의 구조를 명확히 이해할 수 있음
◦
유연성 : 다양한 시계열 데이터에 적용할 수 있는 유연한 모델링 기법
•
BSTS와 칼만 필터 공통점
◦
상태 공간 모델 기반, 숨겨진 상태 변수를 사용하여 시계열 데이터를 모델링 함
•
BSTS와 선형 가우스 모델의 차이점
◦
모델링 접근법
▪
선형 가우스 모델 : 시스템의 선형성과 가우스 잡음을 가정
▪
BSTS : 복잡한 모델링을 위한 다양한 구조적 요소를 베이즈적으로 통합
◦
추론 방법
▪
선형 가우스 모델 : 칼만 필터를 통한 점 추정
▪
BSTS : MCMC(Markov Chain Monte Carlo)를 통한 확률적 추정
•
BSTS 의 장점
◦
유연성 : 다양한 구조적 요소를 포함하여 복잡한 시스템을 모델링
◦
베이즈 추론 : 모델 파라미터와 상태에 대한 불확실성을 자연스럽게 처리
◦
적합 기법 : 사전 분포와 데이터로부터 모델 파라미터를 추정
•
구조 설계 및 파라미터 추정
◦
구조 설계 : 모델에 포함할 트렌드, 계절성, 회귀 요소 등을 정의
◦
파라미터 추정 : 베이즈 추론을 통해 사전 분포와 데이터로부터 모델 파라미터를 추정
•
예시
◦
경제 지표 모델 : GDP 성장률과 실업률을 포함한 경제 지표 모델링
◦
기상 모델 : 온도, 압력, 습도 등의 기상 데이터를 통한 예측 모델링
•
BSTS 모델 적합 과정
◦
사전 확률 및 구조적 모델 정의
▪
구조적 모델 정의
•
트렌드, 계절성, 회귀 요소 포함
•
사전 확률(prior probabilities) 설정
▪
목적 : 시스템에 대한 이미 알려진 사실이나 가설 반영
사전확률과 사후 확률
◦
칼만 필터 적용
▪
상태 추정 갱신
•
관측된 데이터를 바탕으로 상태 추정
•
칼만 필터를 사용하여 현재 상태를 업데이트
▪
목적 : 실시간으로 상태 변수의 최적 추정치 확보
◦
스파이크앤슬랩 변수 선택
▪
변수 선택 방법
•
Spike and slab method를 사용
•
중요한 변수와 중요하지 않은 변수 구분
▪
목적 : 모델의 복잡성을 줄이고 중요한 변수 식별
스파이크앤슬랩 메소드(Spike and Slab Method)
◦
베이즈 모델 평균화(Bayesian Model Averaging)
▪
결과 결합
•
다양한 모델의 결과 결합
•
베이즈 모델 평균화 적용
▪
목적 : 예측의 정확도와 신뢰성 향상
베이즈 모델 평균화(BMA)
7.4.1 코드로 살펴보는 bsts
•
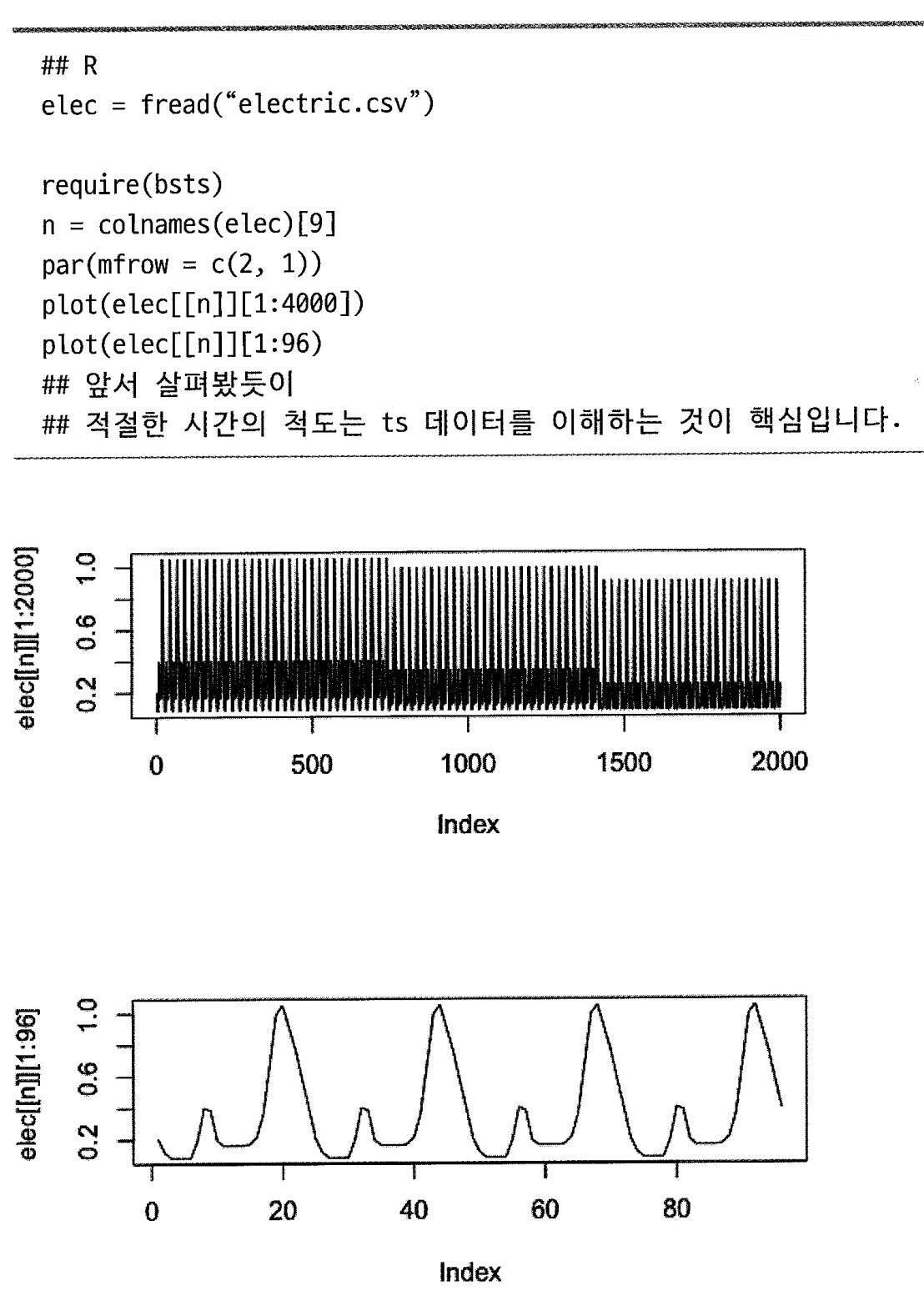
BSTS 패키지인 bsts와 OpenEL.org(http://openei.org/wiki/Main_Page)에서 취득한 개방형 데이터를 사용한 데이터 그래프 (그림 7-8)
OpenEL.org에서 가져온 전력 소비 데이터를 사용
두개의 다른 시간 척도에서 데이터의 변화를 시각화하는 과정을 보여줌.
첫번째 플롯은 긴 시간 척도에서의 데이터를
두번째 플롯은 짧은 시간 척도에서의 데이터를 나타냄
데이터의 시간적 패턴을 이해하는데 도움이 됨
•
(그림 7-8) 상단 그래프 : 모델을 적합시켜야 하는 전체 계열
하단 그래프 : 전체를 짧게 잘라낸 부분집합
⇒일일 패턴을 분명히 보여 줄 수 있는 방법
•
데이터는 명백한 일일 및 요일별 패턴을 보여줌
•
이러한 패턴들은 모델링에서 계절성을 설명하는데 사용됨
•
전체 데이터를 보면 비정상적인 동작이 보임
•
데이터의 추세를 반영해 이런 비정상 동작을 허용하는 모델을 만듬
•
ss <- AddLocalLinearTrend(list(), ele[[n]])
◦
기본 상태 공간 리스트에 로컬 선형 추세 모델을 추가하여 데이터의 추세를 포착함
•
ss <- AddSeasonal(ss, elec[[n]], nseasons = 24, season.duration =1)
◦
하루동안의 24시간 주기 계절성을 상태 공간 모델에 추가하여 일일 패턴을 반영함
•
ss <- AddSeasonal(ss, elec[[n]], nseasons = 7, season.duration = 24)
◦
주 단위의 7일 주기 계절성을 추가하여 요일별 패턴을 반영함
•
지역적 선형 추세(AddLocalLinearTrend)
◦
데이터 추세의 평균과 기울기가 모두 확률보행을 따른다고 가정
◦
모델의 계절성 요소
▪
두 개의 인수 (계절의 개수 & 계절의 길이)
▪
첫번째 요소는 일일 주기를 반영, 매 시간마다 하나의 계절을 가지며 각 계절은 한 시간 지속하도록 설정
▪
두번째 요소는 주간 주기를 반영, 매 요일마다 하나의 계절을 가지며 각 계절은 24시간 지속하도록 설정
◦
일관성의 중요성
▪
정확한 시작 시간보다 데이터의 반복 패턴을 일관되게 반영하는 것이 더 중요함
▪
데이터를 24시간으로 분할하는 방법은 계절성 분석에 적합함
•
bsts 패키지의 장점
◦
사후 확률에 대한 마르코프체인 몬테카를(MCMC)로 계산을 여러 번 수행할 수 있음
◦
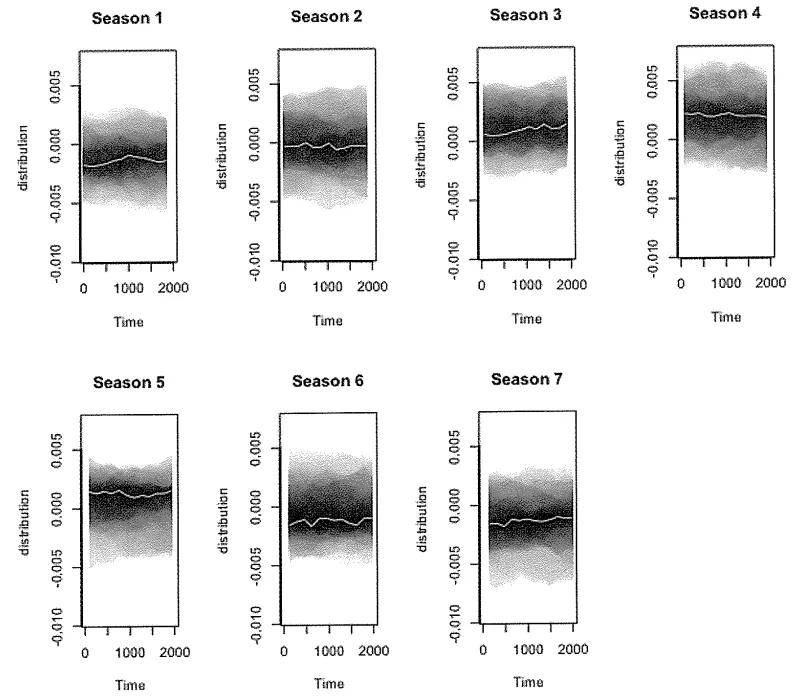
요일별 계절성 요소도 검사할 수 있음 (그림 7-9 및 7-10)
•
(그림 7-9) 요일별 계절성은 서로 다른 요일에 따라 차이가 있다는 것을 보여줌
•
요일별 파라미터별 분포는 요일별 추세가 시간의 흐름에 걸쳐 안정적임을 보여줌
•
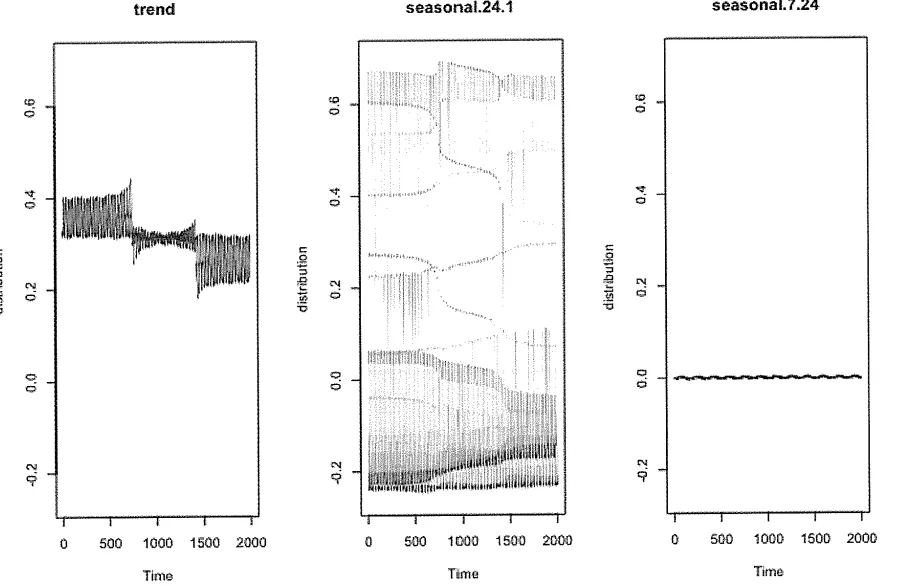
(그림 7-10) 데이터 추세, 일별, 요일별 계절성 요소의 기여도 분포 보여줌
→ 세 요소 더하면 예측값 얻을 수 있음
•
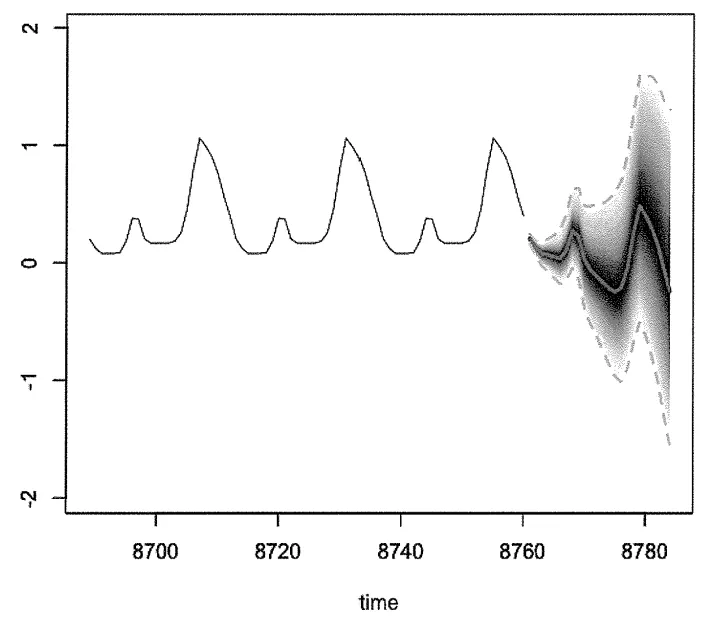
(그림 7-11) 마지막 72시간의 데이터와 예측된 24시간의 데이터의 결합
미래를 예측할 수록 분포가 넓어짐
•
BSTS 패키지의 유용한 옵션
◦
비표준적인 사전 확률을 지정
▪
다양한 사전 확률을 모델에 주입할 수 있음
▪
표준적인 선형 가우스 모델 외에도 비대칭 사전 확률 등 더 많은 옵션을 제공함
◦
회귀 모델 선택에 스파이크앤슬랩 방법을 사용
▪
스파이크앤슬랩을 통해 회귀 모델의 변수 선택 수행할 수 있음
◦
베이즈 모델 평균화를 사용
▪
여러 모델을 결합하여 초기 모델 선택의 불확실성을 설명할 수 있음
사전 확률 : BSTS 에서는 모든 종류의 사전 확률을 모델링에 주입할 수 있음, 칼만 필터의 표준적인 선형 가우스 모델 보다 훨씬 더 많은 옵션을 제공
변수 선택 : 스파이크 슬랩 방법을 사용하여 모델의 변수 선택을 효과적으로 수행할 수 있음
베이즈 모델 평균화 : 여러 모델은 베이즈 모델 평균화로 결합하여 초기 모델 선택과 관련된 불확실성을 설명하는데 도움됨
: