2. 퍼셉트론(Perceptron)

인공 신경망(딥러닝) 분야의 초창기 알고리즘 (by Frank Rosenblatt, 1957)

퍼셉트론은 머신러닝 분야의 신경망의 초창기 알고리즘에 해당된다(출처: Deep Marketer)

2.1 퍼셉트론이란?

•

인공 신경망(Artificial Neural Networks): 사람의 지능을 구현하는 뇌신경 구조와 신호 전달 체계를 모형화

•

퍼셉트론(Perceptron): 사람의 뇌신경을 구성하는 가장 기본 요소인 뉴런 단위의 신호 처리 과정을 모형화

•

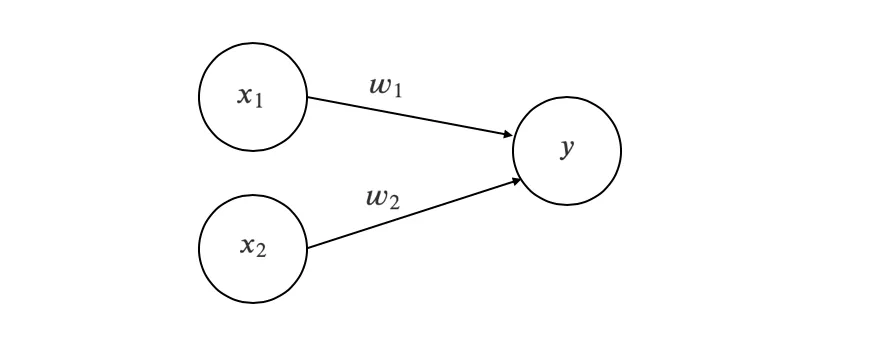
퍼셉트론은 다수의 입력 신호(예: x1,x2)x_1, x_2)x1​,x2​)를 입력으로 받아 하나의 출력 신호(예: yyy)를 생성

◦

1: ‘신호가 흐른다’

◦

0: ‘신호가 흐르지 않는다’

◦

원(circle): 뉴런 또는 노드

◦

가중치(w1,w2w_1,w_2w1​,w2​): 입력 신호의 세기를 조절하는 역할

퍼셉트론의 기본 구조: 입력 신호(x1, x2), 가중치(w1, w2), 출력 신호(y)

•

출력 신호(yyy): 뉴런에서 전달한 신호의 총합이 정해진 한계를 넘을 때 1을 출력함

◦

이를 “뉴런이 활성화(activate)한다.” 라고 표현

◦

정해진 한계 = 임계값(threshold, θ\thetaθ)

y=\begin{cases} 0 & (w_1x_1+w_2x_2 \leq \theta)\\ 1 & (w_1x_1+w_2x_2\gt \theta) \end{cases}

◦

가중치의 역할이 중요함. 가중치가 크다 → 해당 입력 신호가 중요함

2.2 단순한 논리 회로

2.2.1 AND 게이트

•

입력된 두 개의 신호가 모두 1일 때, 1의 신호 값을 출력

•

나머지 경우는 모두 0의 신호 값을 출력

•

퍼셉트론으로 AND 게이트 구현하기: w1,w2,θw_1, w_2, \theta w1​,w2​,θ 를 결정

x1	x2	y
0	0	0
0	1	0
1	0	0
1	1	1

•

[Ex] 퍼셉트론으로 AND 게이트를 구현하기 위해 매개변수 값들의 예를 제시하라.

◦

∴w1=0.5,w2=0.5,θ=0.9\therefore w_1=0.5, w_2=0.5, \theta=0.9∴w1​=0.5,w2​=0.5,θ=0.9  즉,  (0.5,0.5,0.9)(0.5,0.5,0.9)(0.5,0.5,0.9)

◦

x1,x2=0x_1,x_2=0x1​,x2​=0 일 때, 0<0.90<0.90<0.9 이므로 000을 출력

◦

x1=0,x2=1x_1=0, x_2=1x1​=0,x2​=1 일 때, 0.5<0.90.5 < 0.90.5<0.9 이므로 000을 출력

◦

x1=1,x2=0x_1=1, x_2=0x1​=1,x2​=0 일 때, 0.5<0.90.5 < 0.90.5<0.9 이므로 000을 출력

◦

x1=1,x2=1x_1=1, x_2=1x1​=1,x2​=1 일 때, 0.5+0.5>0.90.5+0.5 > 0.90.5+0.5>0.9 이므로 111을 출력

2.2.2 NAND 게이트와 OR 게이트

•

NAND 게이트는 Not AND를 의미하며 AND 게이트의 출력과 정반대

•

[Ex] 퍼셉트론으로 NAND 게이트를 구현하기 위해 매개변수 값들의 예를 제시하라.

◦

∴(−0.3,−0.5,−0.8)\therefore(-0.3,-0.5,-0.8)∴(−0.3,−0.5,−0.8)

x1	x2	y
0	0	1
0	1	1
1	0	1
1	1	0

•

OR 게이트는 두 입력 신호 중 하나 이상 1일 때 1의 신호 값을 출력

•

[Ex] 퍼셉트론으로 OR 게이트를 구현하기 위해 매개변수 값들의 예를 제시하라.

◦

∴(0.2,0.2,0.1)\therefore(0.2,0.2,0.1)∴(0.2,0.2,0.1)

x1	x2	y
0	0	0
0	1	1
1	0	1
1	1	1

•

학습과 기계학습의 정의

◦

학습(learning)이란 가중치(매개변수)를 적절하게 선택하는 작업 

◦

퍼셉트론 기본 모델에서는 사람이 진리표(학습 데이터)를 보고 적절한 매개변수를 직접 선택

◦

그러나, 기계학습에서는 매개변수 선택을 컴퓨터가 자동으로 수행

◦

기계학습에서 사람은 퍼셉트론의 구조(모델)를 고민하고 컴퓨터에 학습할 데이터를 주는 역할을 수행

2.3 퍼셉트론 구현하기

•

w1,w2w_1, w_2w1​,w2​ : 가중치, 각 입력 신호가 결과에 주는 영향력(중요도)조절 매개변수

•

bbb : 편향, 뉴런의 활성화(=1) 조건을 조정하는 매개변수

◦

−θ-\theta−θ를 편향 bbb로 치환

◦

 bbb=-0.1일 때, 각 입력 신호에 가중치를 곱한 값들의 합이 0.1을 초과하면 뉴런 활성화

2.3.1 간단한 구현부터

•

입력 신호 x1, x2에 가중치를 곱한 후 합한 값이 θ\thetaθ를 넘으면 1, 넘지 않으면 0 출력

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1

# 출력
AND(0, 0) # 0
AND(1, 0) # 0
AND(0, 1) # 0
AND(1, 1) # 1
Python
복사

2.3.2 가중치와 편향 도입

import numpy as np

x = np.array([0, 1]) # 입력
w = np.array([0.5, 0.5]) # 가중치
b = -0.7 # 편향

# 출력
w*x # [0.  0.5]
np.sum(w*x) # 0.5
np.sum(w*x)+b # -0.19999999999999996
Python
복사

2.3.3 가중치와 편향 구현하기

•

AND 게이트

◦

입력 신호 x1, x2에 가중치를 곱한 값과 편향을 합한 값이 θ\thetaθ를 넘으면 1, 넘지 않으면 0 출력

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1
Python
복사

•

NAND 게이트

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5]) # AND와는 가중치(w,b)만 다름
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1
Python
복사

•

OR 게이트

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1
Python
복사

2.4 퍼셉트론의 한계

2.4.1 도전! XOR 게이트

•

XOR  게이트

◦

배타적 논리합 논리 회로

▪

배타적 논리합 : 두 개의 명제 중 하나만 참일 때 결과값이 참인 논리 연산

x1	x2	y
0	0	0
1	0	1
0	1	1
1	1	0

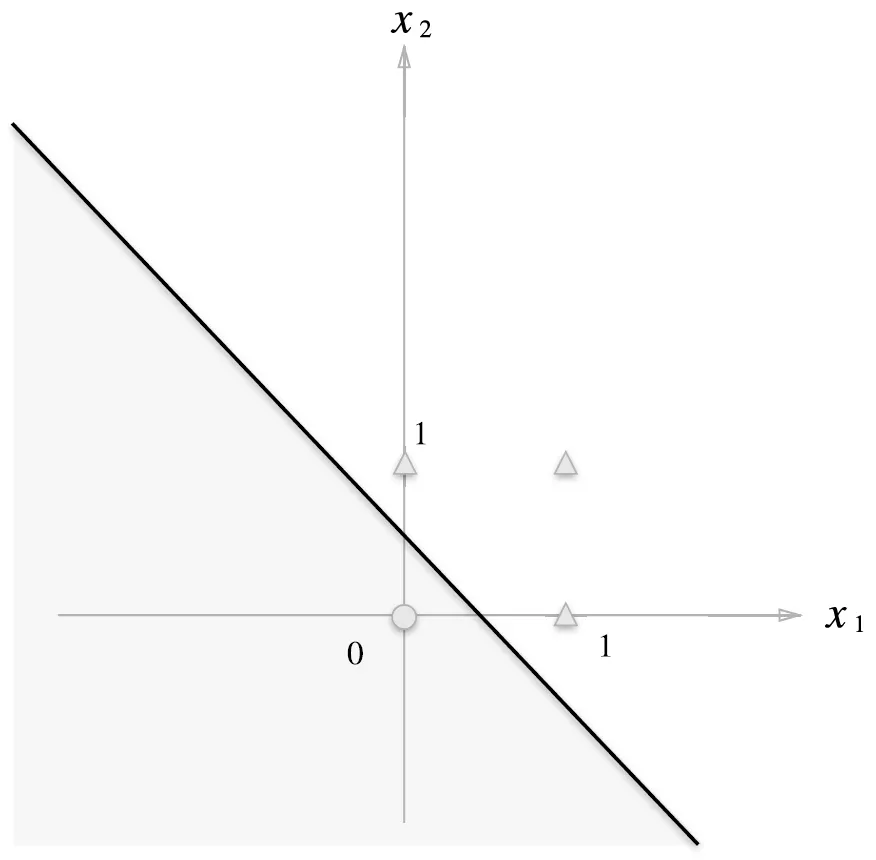
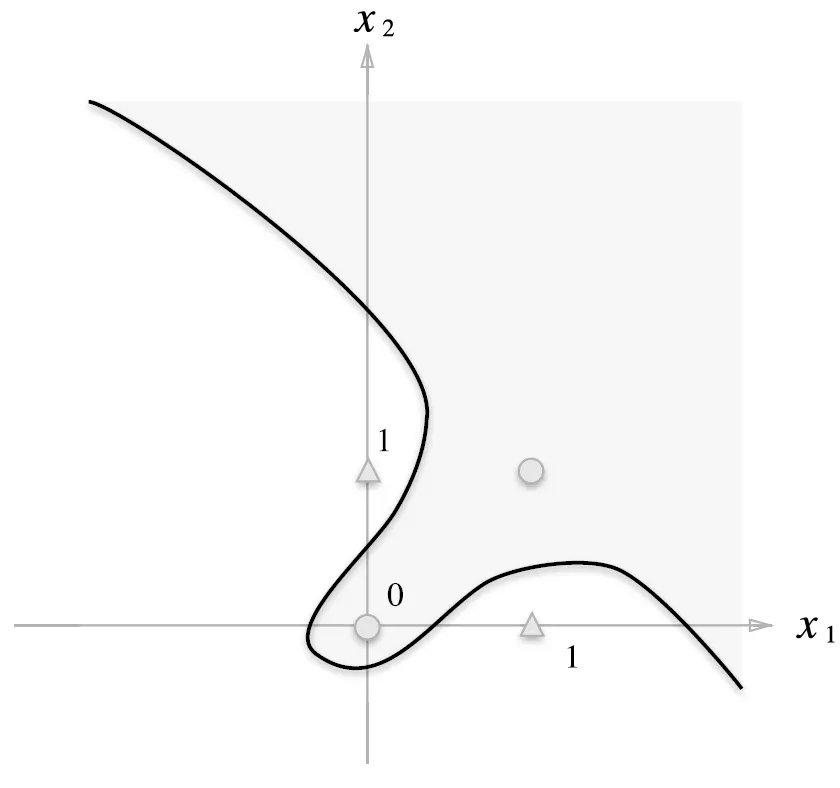
2.4.2 선형과 비선형

•

XOR 게이트를 퍼셉트론으로 구현 → 불가능

◦

선형으로 분리 가능한 AND, OR과 달리 XOR은 비선형으로만 분리 가능하기 때문 

▪

선형 : 직선의 영역

▪

비선형 : 곡선의 영역

OR게이트 영역 구분(회색 영역=0) → 퍼셉트론 O

XOR게이트 영역 구분 → 퍼셉트론 X

“단층 퍼셉트론으로는 XOR 게이트를 표현할 수 없다” ⇒ 다층 퍼셉트론

2.5 다층 퍼셉트론이 출동한다면

•

다층 퍼셉트론 : 층이 여러 개인 퍼셉트론

•

가중치를 갖는 층을 하나의 층으로 봄(결과 yyy는 층에 포함하지 않음)

2.5.1 기존 게이트 조합하기

•

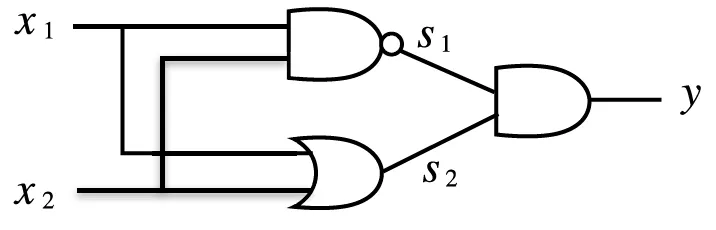
AND, NAND, OR 게이트 기호

•

AND, NAND, OR 게이트 조합으로 표현한 XOR 게이트

◦

x1,x2x_1, x_2x1​,x2​을 입력으로 받은 NAND, OR 게이트의 출력이 다시 AND의 입력이 됨

•

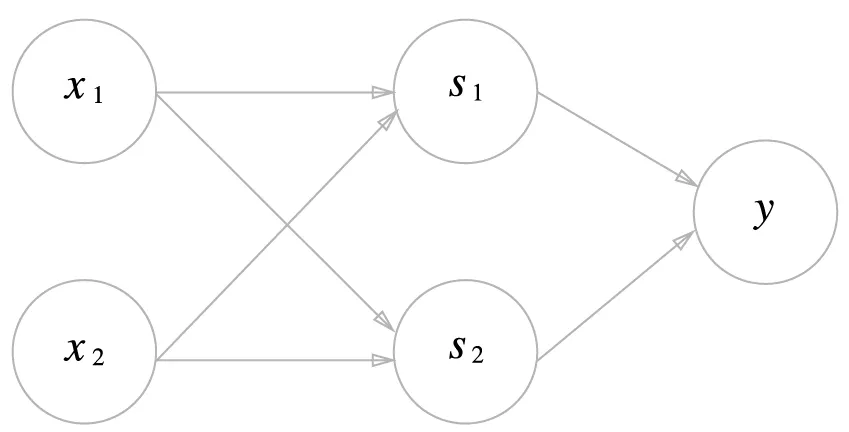
뉴런으로 표현한 XOR의 퍼셉트론

◦

첫 번째 층의 두 뉴런이 입력 신호(x1,x2)(x_1, x_2)(x1​,x2​)를 받아 출력한 값을 두 번째 층으로 보내면, 두 번째 층은 받은 신호(S1,S2)(S_1, S_2)(S1​,S2​)를 입력으로 받아 최종적으로 y\mathrm yy를 출력한다.

•

XOR 게이트 진리표

x1	x2	s1	s2	y
0	0	1	0	0
1	0	1	1	1
0	1	1	1	1
1	1	0	1	0

2.5.2 XOR 게이트 구현하기

def XOR(x1, x2):
		s1 = NAND(x1, x2)
		s2 = OR(x1, x2)
		y = AND(s1, s2)
		return y
Python
복사

XOR(0, 0) # 0
XOR(1, 0) # 1
XOR(0, 1) # 1
XOR(1, 1) # 0
Python
복사

2.6 NAND에서 컴퓨터까지

•

NAND 조합만으로도 컴퓨터를 만들 수 있다

•

(The Elements of Computin Systems: Building a Modern Computer from First Principles(The MIT Press, 2005) → 실제 NAND로 테트리스가 작동하는 컴퓨터 제작

2.7. 정리

•

퍼셉트론은 입출력을 갖춘 알고리즘이다. 입력을 주면 정해진 규칙에 따른 값을 출력한다.

•

퍼셉트론에서는 ‘가중치’와 ‘편향’을 매개변수로 설정한다.

•

퍼셉트론으로 AND, OR 게이트 등의 논리 회로를 표현할 수 있다.

•

XOR 게이트는 단층 퍼셉트론으로는 표현할 수 없다.

•

2층 퍼셉트론을 이용하면  XOR 게이트를 표현할 수 있다.

•

단층 퍼셉트론은 직선형 영역만 표현할 수 있고, 다층 퍼셉트론은 비선형 영역도 표현할 수 있다.

•

다층 퍼셉트론은 (이론상) 컴퓨터를 표현할 수 있다.