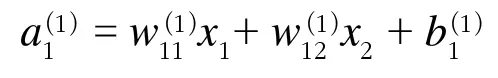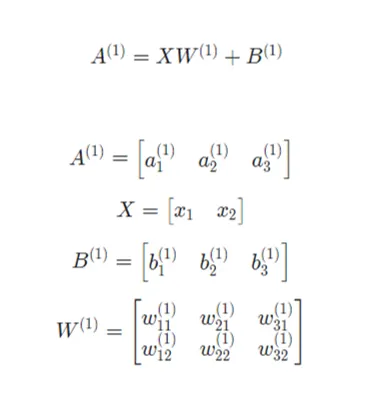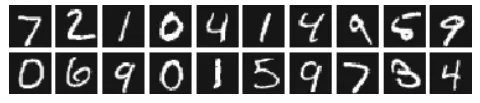3. 신경망

•

퍼셉트론: 다층 퍼셉트론으로 복잡한 함수 또는 기능 구현 가능. 그러나, 가중치를 설정하는 작업은 사람에 의해 수행됨

•

신경망(Neural Networks): 퍼셉트론에 활성화 함수(3장), 손실 함수(4장), 역전파(5장)의 개념이 추가되어 진정한 기계학습의 개념이 구현됨

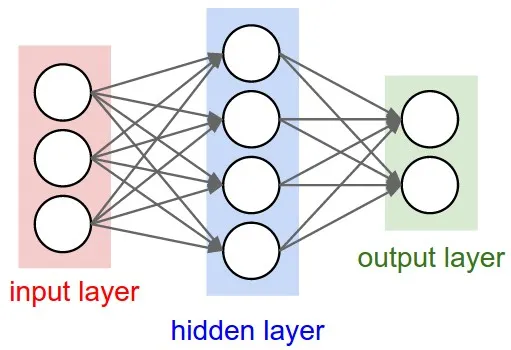
3.1.1 신경망의 예

•

입력층(Input layer) : 입력을 받는 층

•

은닉층(Hidden layer) : 계산이 일어나는 층으로, 입력층과 출력층 사이에 존재

◦

입력층, 출력층과 다르게 사용자가 볼 수 없음(black-box)

•

출력층(Output layer) : 결과를 출력하는 층

3.1.2 퍼셉트론 복습

입력 신호의 총합이

h(x)

라는 함수를 거쳐 변환되어, 변환된 값이

\mathrm {y}

의 출력이 됨을 보여줌.

h(x)

함수는 입력이 0을 넘으면 1을 돌려주고 그렇지 않으면 0을 돌려줌. 결과적으로 위의 식과 동일

⇒ 겹치는 부분이니까 빼도 좋을 듯

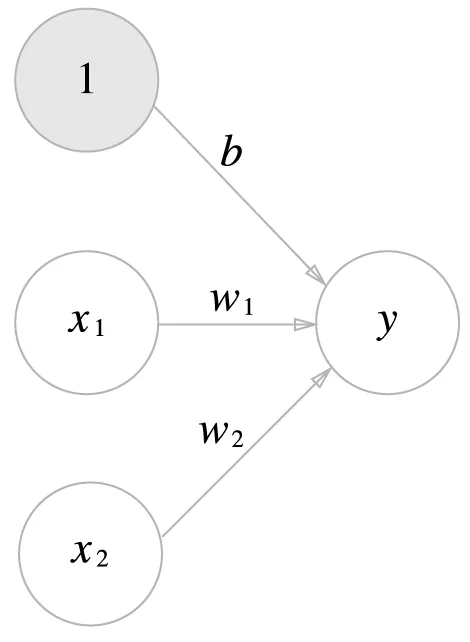
편향을 명시한 퍼셉트론 (뉴런 추가 : 가중치 b, 입력 1)

\mathrm {y} = \begin{cases} 0\ (b+w_1x_1 + w_2x_2 \leq 0) \\ 1\ (b+w_1x_1 + w_2x_2 > 0) \end{cases}

b : 편향을 나타내는 매개 변수 (뉴런 활성화 제어)

w_1, w_2 : 각 신호의 가중치 (신호 영향력 제어)

\mathrm {y} = h(b+w_1x_1 + w_2x_2) \\ h(x) = \begin{cases} 0\ (x \leq 0) \\ 1\ (x > 0) \end{cases}

3.1.3 활성화 함수의 등장

•

활성화 함수(Activation function) : 입력 신호의 총합을 출력 신호로 변환하는 함수

◦

입력 신호의 총합이 활성화를 일으키는 지를 정하는 역할

◦

입력값의 총합(가중치와 입력의 합)을 받아 뉴런의 출력값 결정

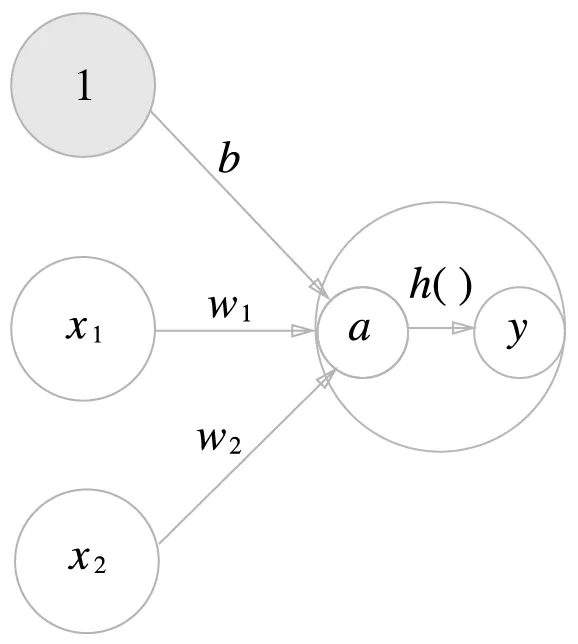
활성화 함수의 처리 과정

a = b + w_1 x_1 + w_2 x_2 \\ \mathrm {y} = h(a)

•

aaa를 함수 h()h()h()에 넣어 y\mathrm {y}y 출력 

•

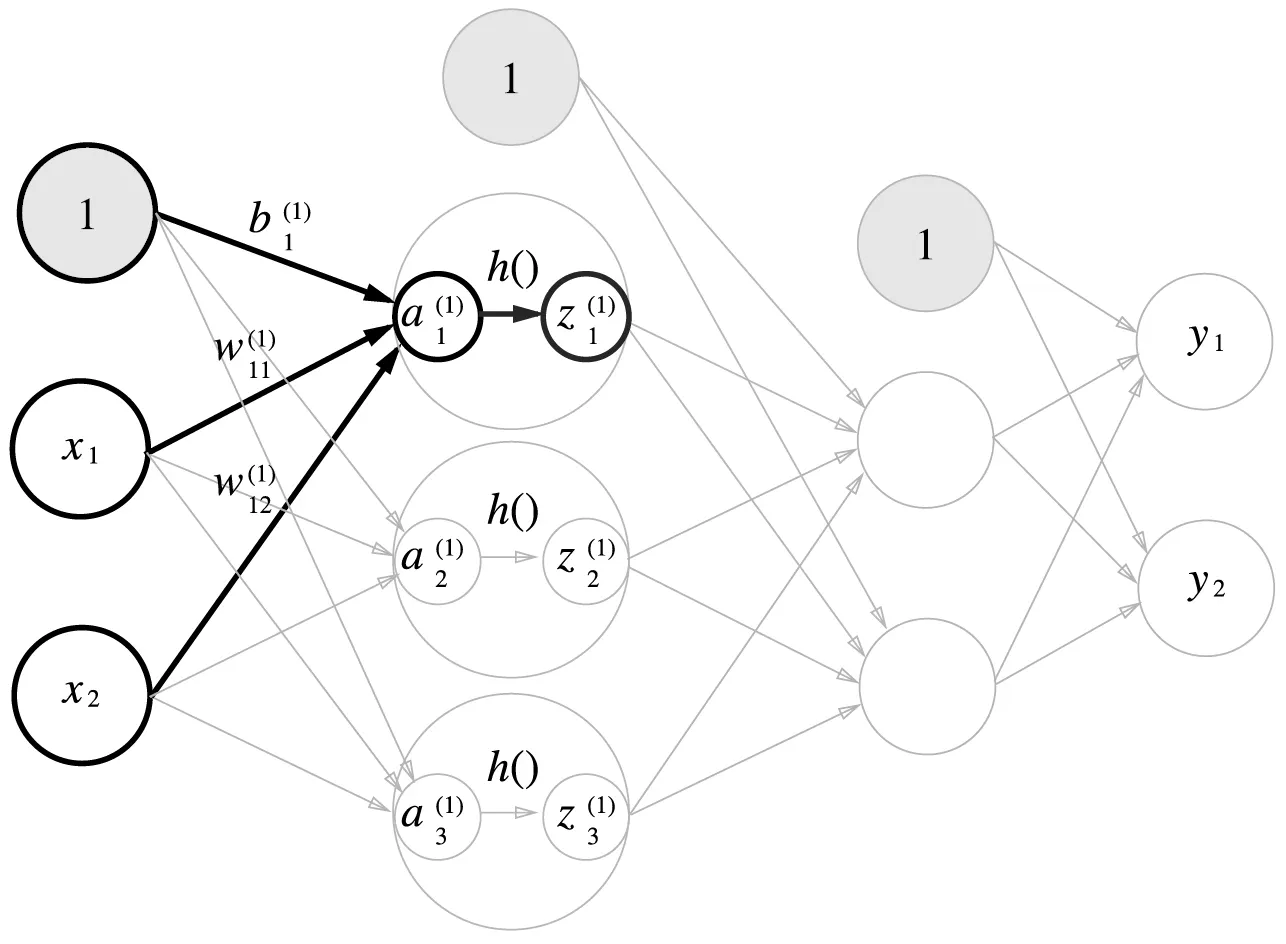
 aaa : 가중치가 적용된 입력 신호와 편향의 총합

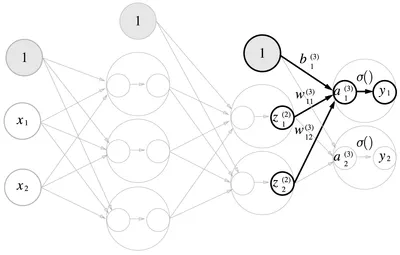
가중치 신호를 조합한 결과가

a

라는 노드가 되고, 활성화 함수

h()

를 통과해

\mathrm {y}

라는 노드로 변환

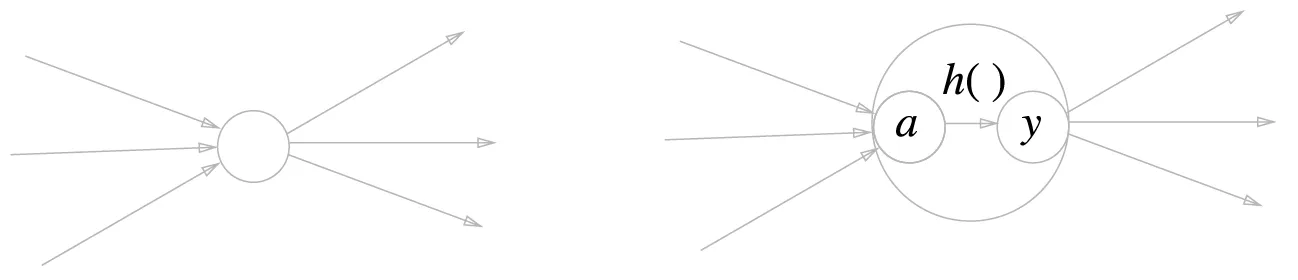
뉴런 = 노드

왼쪽은 일반적인 뉴런, 오른쪽은 활성화 처리 과정을 명시한 뉴런

3.2 활성화 함수

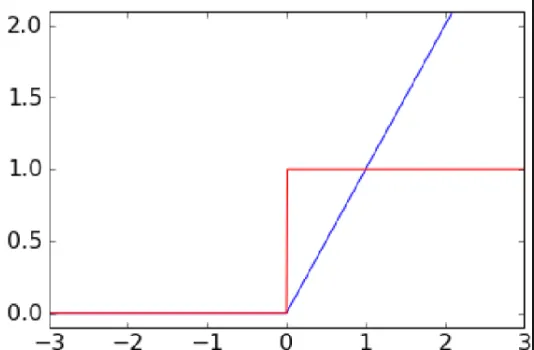
계단 함수(Step function) : 임계값을 경계로 출력이 바뀌는 함수

•

퍼셉트론에서는 활성화 함수로 계단 함수를 이용

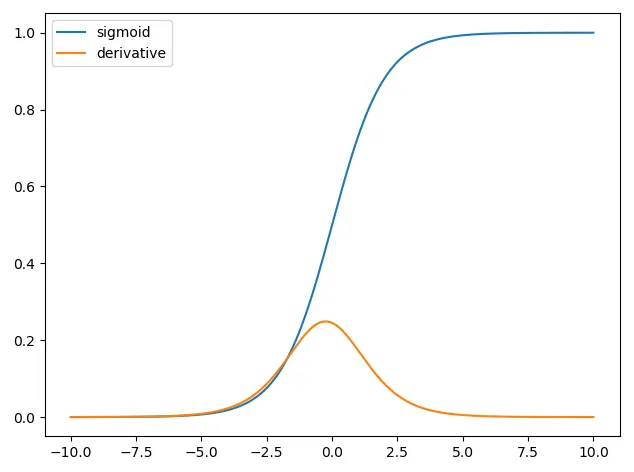
3.2.1 시그모이드 함수

시그모이드 함수(Sigmoid function)

•

S자형 곡선 또는 시그모이드 곡선을 갖는 함수

◦

시그모이드(Sigmoid) : 그리스 문자 ‘sigma’의 S와 같은 모양 →  sigma(ς) + -oid(~같은)

•

입력값을 0과 1 사이의 값으로 변환

◦

입력값이 0일 때 0.5 반환

f(x) = {1 \over 1+\mathrm {exp}(-x)}

•

exp(−x)\mathrm {exp}(-x)exp(−x) : e−xe^{-x}e−x를 뜻하며 eee는 자연 상수로 2.7182와 같은 값을 갖는 실수. 

시그모이드 함수에 만약 1.0과 2.0 입력하면

h(1.0) = 0.731..., h(2.0) = 0.880...

과 같은 특정 값 출력

3.2.2 계단 함수 구현하기

•

입력이 0을 넘으면 1 출력 넘지 않으면 0 출력

def step_fuction(x):
    if x > 0:
        return 1
    else:
        return 0
Python
복사

step_function(2.0) # 1
Python
복사

•

Numpy 배열을 인수로 넣을 수 있도록 코드 수정

def step_function(x):
    y = x > 0
    return y.astype(np.int)
Python
복사

step_function(np.array([1.0, 2.0])) # array([1, 1])
step_function(np.array([2.0])) # array([1])
step_function(2.0) # 오류 : astype -> astype은 Numpy 배열의 데이터 타입을 변경하는 메서드이기 때문
Python
복사

구현 과정 상세

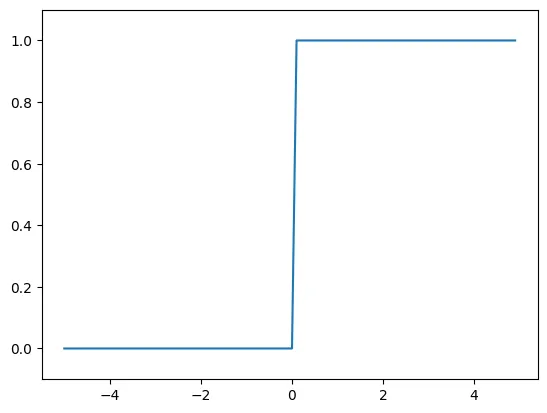
3.2.3 계단 함수의 그래프

def step_function(x):
    return np.array(x > 0, dtype=np.int)
Python
복사

# 시각화
x = np.arange(-5, 5.0, 0.1) # -5.0 ~ 5.0 전까지 0.1 간격의 Numpy array 생성 [-5.0, -4.9 ... 4.9]
y = step_function(x)

plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y축 범위 지정
plt.show()
Python
복사

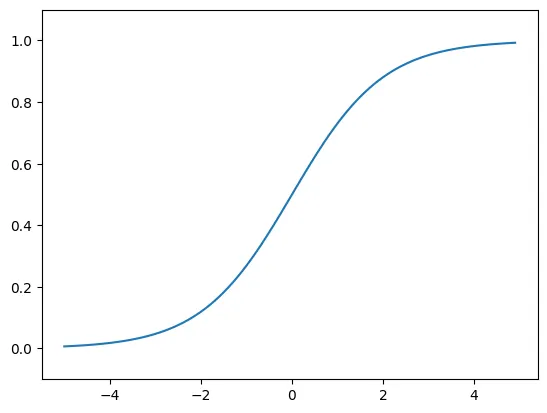
3.2.4 시그모이드 함수 구현하기

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
Python
복사

x = np.array([-1.0, 1.0, 2.0])
sigmoid(x)

# 브로드캐스트 기능 덕분에 가능
Python
복사

Broadcast

x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)

plt.plot(x,y)
plt.ylim(-0.1, 1.1) # y축 범위 지정
plt.show()
Python
복사

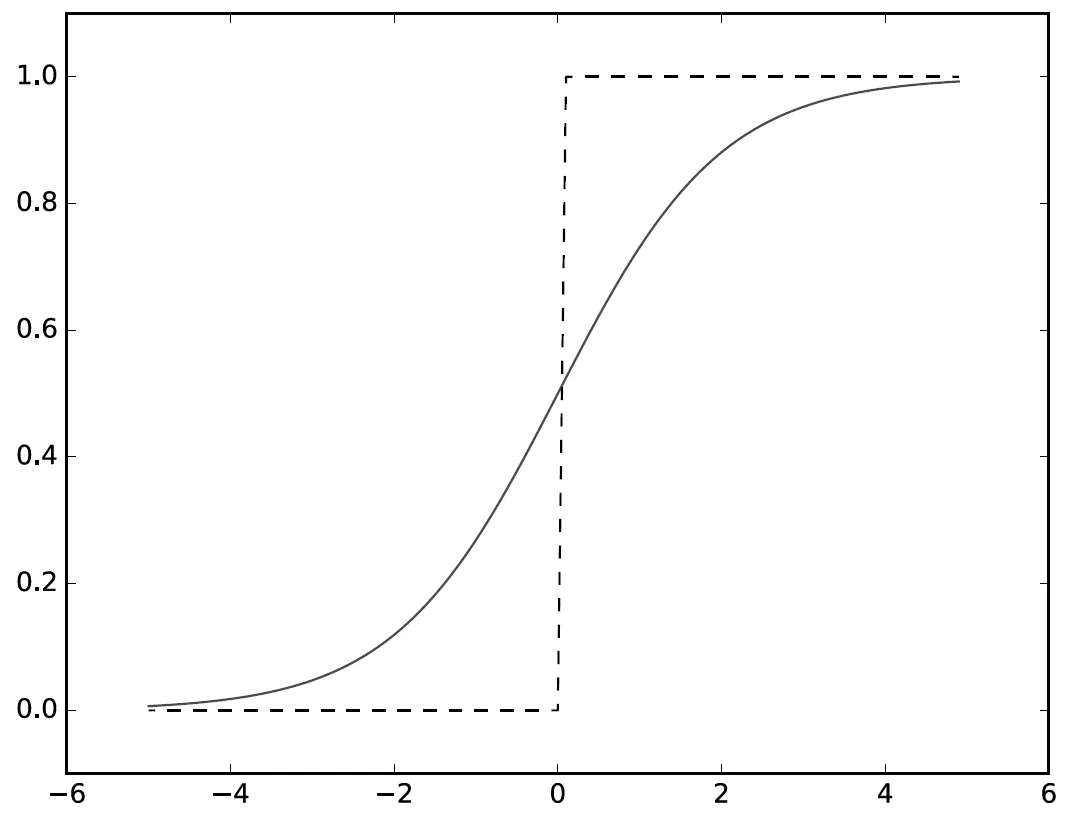
3.2.5 시그모이드 함수와 계단 함수 비교

•

계단 함수는 0과 1 중 하나의 값을, 시그모이드 함수는 실수(0.731…, 0.880… 등)를 출력

◦

퍼셉트론에서는 0 또는 1의 값이, 신경망에서는 연속적인 실수가 흐름

•

두 함수 모두 입력이 중요하면 큰 값을, 중요하지 않으면 작은 값을 출력

◦

입력이 크면 1 또는 1에 가까운 값을, 입력이 작으면 0 또는 0에 가까운 값 출력(0~1의 범위)

3.2.6 비선형 함수

비선형 함수: ‘선형이 아닌’ 함수 (직선 1개로 그릴 수 없는 함수)

•

선형 함수는 출력이 입력의 상수배만큼 변하며 직선에 해당 f(x)=ax+b (a,bf(x) = ax + b\ ( a, bf(x)=ax+b (a,b는 상수) 

신경망에서 비선형 함수를 사용해야 하는 이유? → 선형 함수를 이용하면 신경망의 층의 의미가 없음

h(x) = cx

\mathrm y(x) = h(h(h(x)))

\mathrm y(x) = c*c*c*x

\mathrm y(x) = ax

a = c^3

3.2.7 RELU 함수

ReLU(Rectified Linear Unit)

•

입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수

•

Rectify : 정류하다 → 교류(전파)를 직류로 바꾸다

h(x) = \begin{cases} x\ (x> 0) \\ 0\ (x\leq 0)\end{cases}

def relu(x):
    return np.maximum(0, x)
Python
복사

relu(3) # 3
relu(0) # 0
relu(-1) # 0
Python
복사

3.3 다차원 배열의 계산

3.3.1 다차원 배열

다차원 배열 : ‘숫자의 집합’을 N차원으로 나열하는 것

A = np.array([1, 2, 3, 4])
B = np.array([[1,2], [3,4], [5,6]])

print(A)
print(B)

# 출력
[1 2 3 4]

[[1 2]
 [3 4]
 [5 6]]
Python
복사

# 배열 차원 확인
np.ndim(A)) # 1
np.ndim(B)) # 2

# 배열 형태 확인 -> 튜플(차원 크기 변경을 방지하고 통일된 형태의 결과를 반환하기 위해)
A.shape # (4,)
A.shape[0] # 4

B.shape # (3, 2) -> 2차원 배열(3*2)
B.shape[0] # 3
Python
복사

•

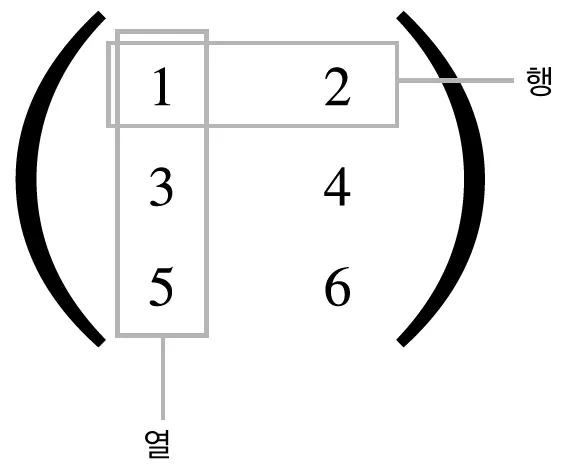
행렬(matrix) : 2차원 배열

◦

가로(row) : 행

◦

세로(column) : 열(차원)

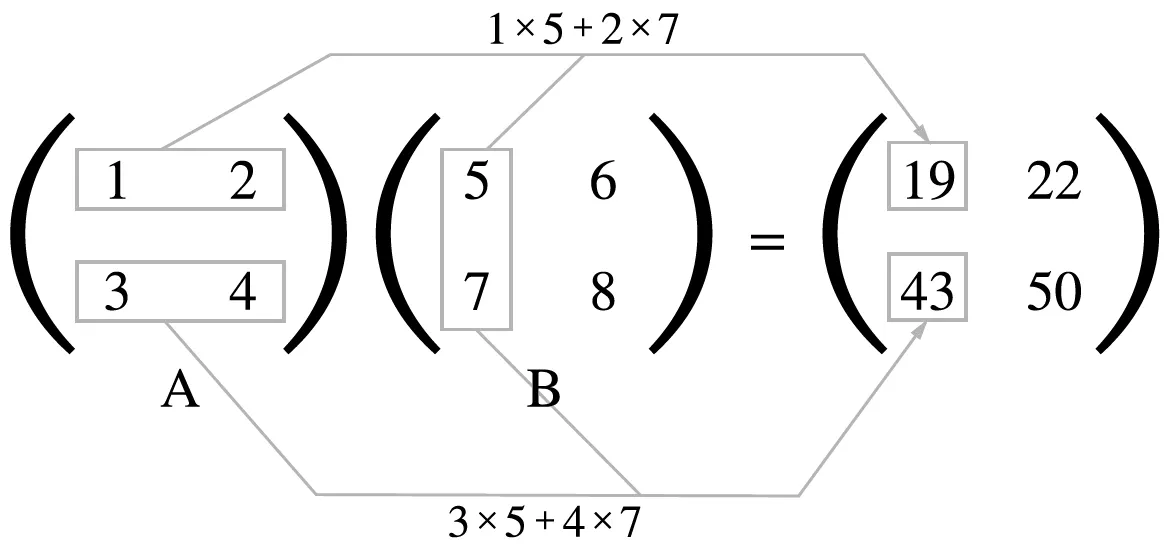
3.3.2 행렬의 곱

•

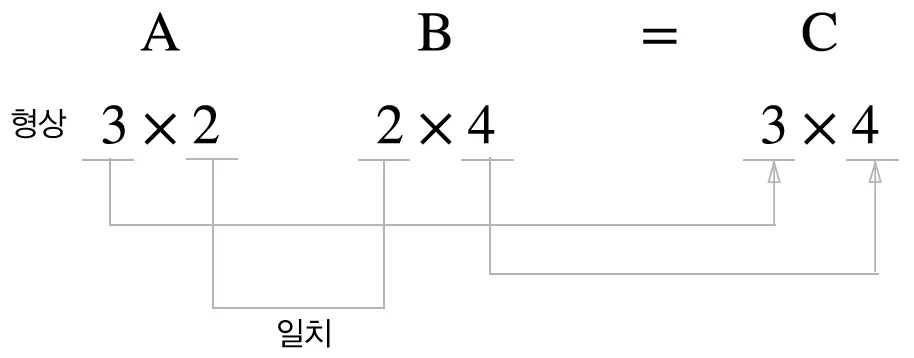
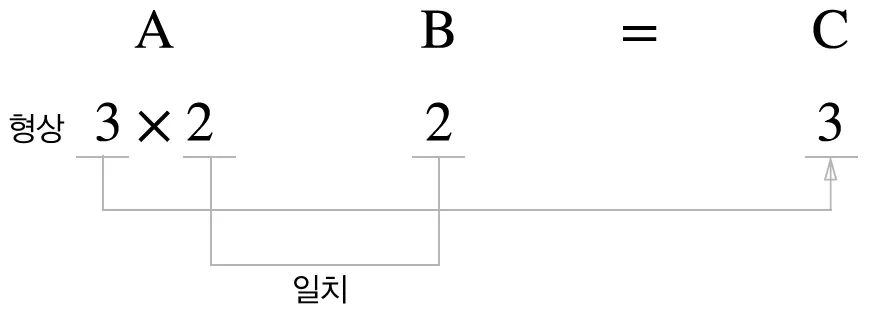
왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소 별로 곱함

◦

두 행렬(A, B)를 곱할 때 A의 행의 수와 B행의 열의 수가 일치해야 함

"""
행렬 곱하기(두 행렬의 크기 일치, 대응 차원 일치)
"""
A = np.array([[1,2], [3,4]])
B = np.array([[5,6], [7,8]])

np.dot(A, B) 

# 출력
array([[19, 22],
       [43, 50]])
Python
복사

"""
행렬 곱하기(두 행렬의 크기 일, 대응 차원 불일치)
"""
A = np.array([[1,2,3], [4,5,6]])
B = np.array([[1,2], [3,4], [5,6]])

np.dot(A, B)

# 출력
array([[22, 28],
       [49, 64]])
Python
복사

"""
행렬 곱하기(두 행렬의 크기 불일치, 대응 차원 불일치)
"""
A = np.array([[1,2,3], [4,5,6]])
C = np.array([[1,2], [3,4]])

# 출력 - 오류 발생
np.dot(A, C)
Python
복사

"""
행렬 곱하기(1차원과 2차원)
"""
A = np.array([[1,2], [3,4],[5,6]])
B = np.array([7,8])

np.dot(A,B) 

# 출력 
array([23, 53, 83])
Python
복사

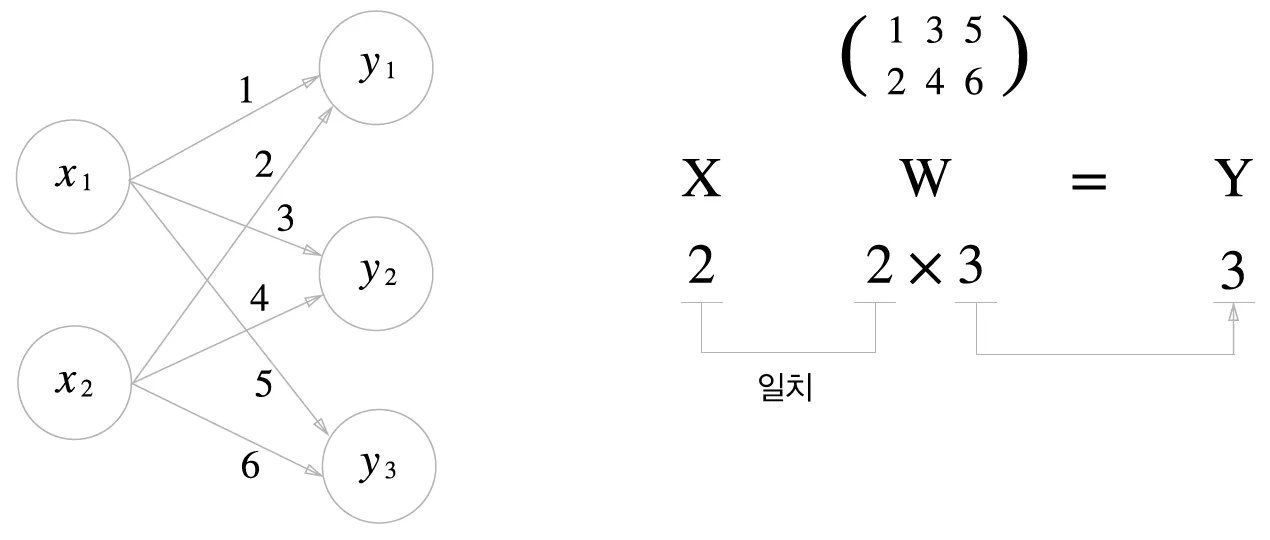
3.3.3 신경망에서의 행렬 곱

•

Numpy 행렬을 사용해 신경망 구현

X = np.array([1,2])
W = np.array([[1,3,5], [2,4,6]])

Y = np.dot(X, W)

print(Y) 

# 출력
[ 5 11 17]
Python
복사

3.4 3층 신경망 구현하기

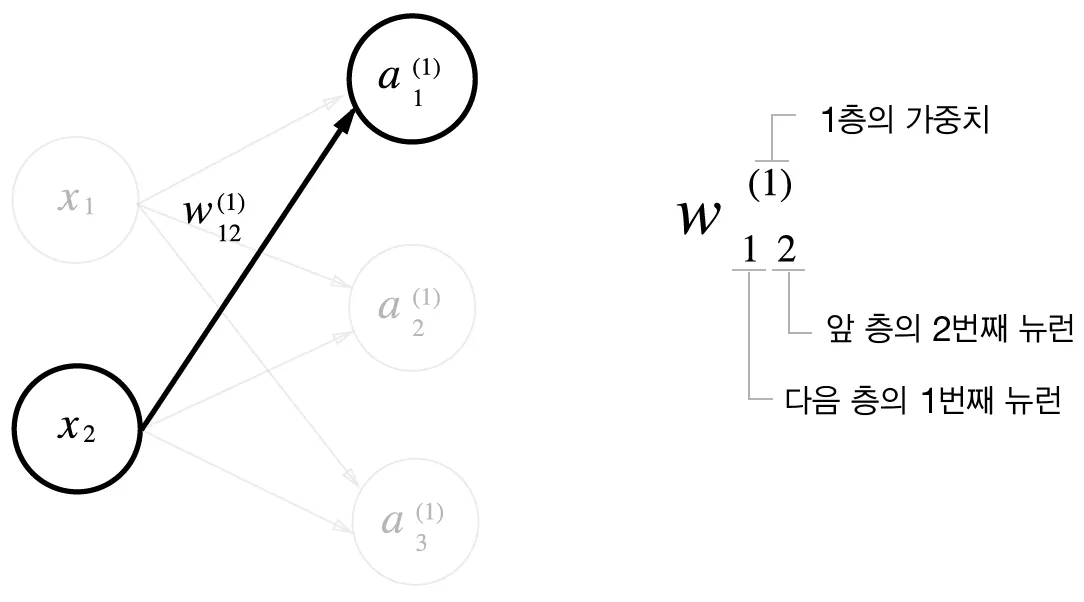
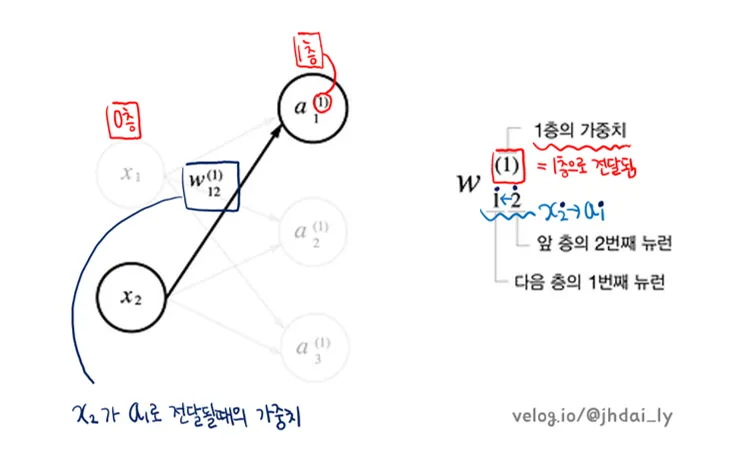
3.4.1 표기법 설명

key point

: 신경망에서의 계산을 행렬 계산으로 정리할 수 있다.

→ 신경망 각 층의 계산은 행렬의 곱으로 처리함

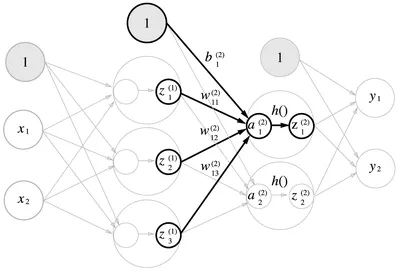
3.4.2 각 층의 신호 전달 구현하기

<1층의 첫 번째 뉴런으로 가는 신호>

인공신경망의 작동 방식을 스칼라나 행렬을 통해 표현할 수 있다고 한다.

◦

스칼라 표현

◦

행렬 표현

그렇다면 왜 스칼라와 행렬을 사용해서 모두 표현할 수 있는데, 왜 우리는 numpy라는 라이브러리, 즉 행렬의 곱셈을 통해 이를 구현하려고 할까?

그리고 행렬의 곱을 이용하면 식을 간소화할 수 있다는 의미는 무엇일까?

만약에 w1~w100까지 1개의 층에 가중치가 100개가 있다고 가정해보자.

우리가 스칼라를 통해 이를 구현하려면 for 문을 통해 각 가중치를 입력 값에 적용하고,

결과를 누적하여 계산하는 방식으로 사용해야 할 것이다.

result = 0
for i in range(100):
  result += weights[i] * input_values[i]
Python
복사

하지만, numpy 라이브러리를 사용하면, 코드가 훨씬 간결해지고 최적화된 행렬 연산을 통해 빠르게 실행된다고 한다.

import numpy as np

#weights = np.array(weights)
#input_values = np.array(input_values)
result = np.dot(weights, input_values)
Python
복사

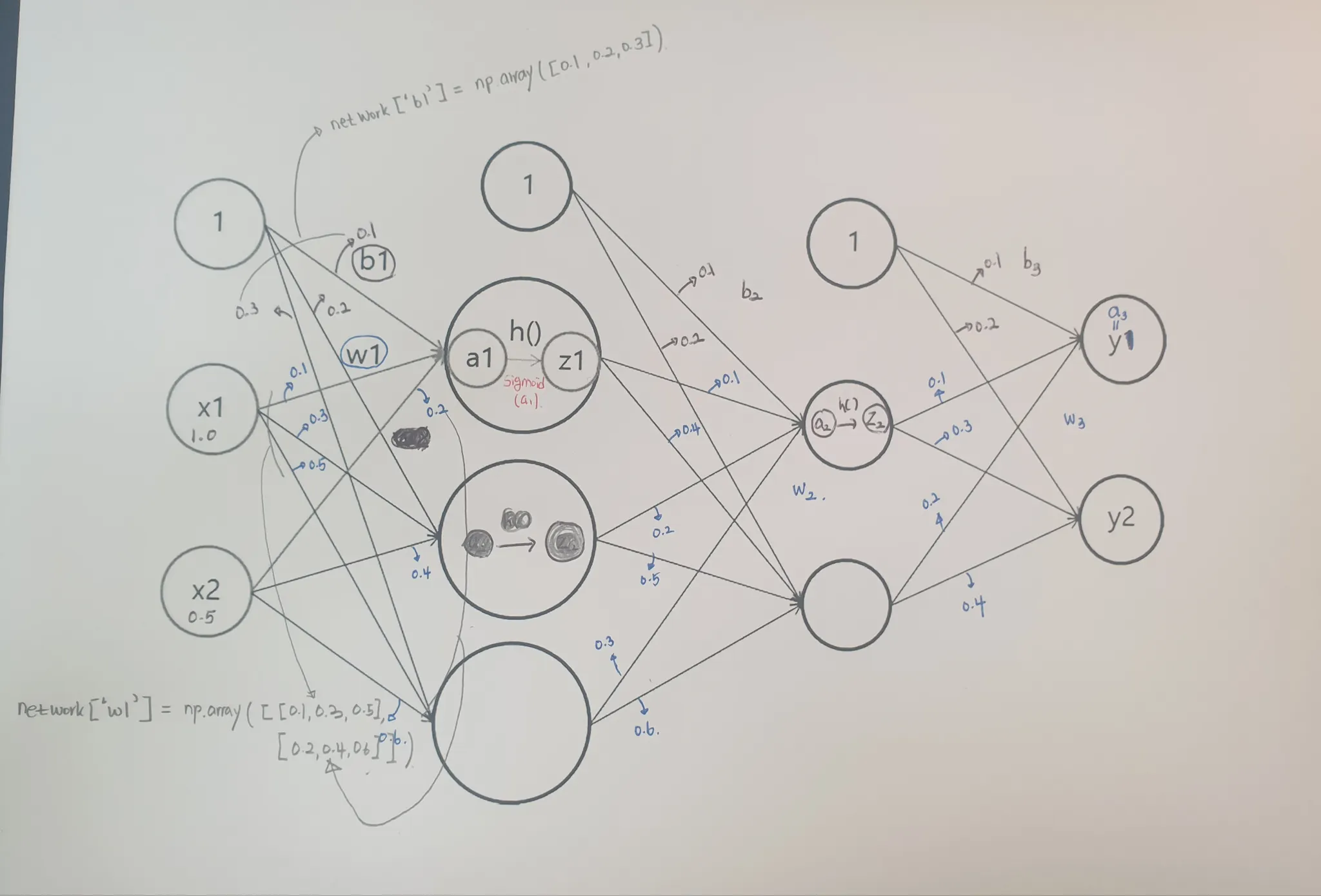
<코드 구현해보기>

import numpy as np
#0층 -> 1층

X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5], [0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])

A1 = np.dot(X,W1) + B1

Z1 = sigmoid(A1)
#def Sigmoid(x):
	#return 1 / (1+np.exp(-x))
Python
복사

#1층 -> 2층
W2 = np.array([[0.1,0.4], [0.2,0.5], [0.3,0.6]])
B2 = np.array([0.1, 0.2])

A2 = np.dot(Z1,W2) + B2
Z2 = sigmoid(A2)
Python
복사

W3 = np.array([[0.1,0.3],[0.2,0.4]])
B3 = np.arrray[0.1,0.2])

A3 = np.dot(Z2,W3) + B3
Y= A3
#def identity_function(x):
	#return x
#Y = identity_function(A3)
Python
복사

3.4.3 구현 정리

import numpy as np

def sigmoid(x):
  return 1 / (1 + np.exp(-x))

#def identity_function(x):
  #return x

#network를 하나의 딕셔너리로 저장하기 -> 가중치와 편향 초기화

def init_network():
  network ={}
  network['W1'] = np.array([[0.1, 0.3, 0.5],[0.2,0.4,0.6]])
  network['b1'] = np.array([0.1,0.2,0.3])

  network['W2'] = np.array([[0.1, 0.4],[0.2,0.5],[0.3,0.6]])
  network['b2'] = np.array([0.1,0.2])

  network['W3'] = np.array([[0.1, 0.3],[0.2,0.4]])
  network['b3'] = np.array([0.1,0.2])
  
  return network

#각 layer로 신호 전달하는 함수

def forward(network , x):
  W1,W2,W3 = network['W1'], network['W2'], network['W3']
  b1,b2,b3 = network['b1'], network['b2'], network['b3']
  
  a1 = np.dot(x,W1) + b1
  z1 = sigmoid(a1)

  a2=  np.dot(z1,W2) + b2
  z2 = sigmoid(a2)

  a3 = np.dot(z2,W3) + b3
  
  # y = identity_function(a3)
  #return y
  
  return a3

network = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
print(y)
JavaScript
복사

3.5 출력층 설계하기

기계학습 문제: 분류(classification)와 회귀(regression)

•

분류: 데이터가 속한 클래스(class)를 예측하는 문제이며, 분류 모델의 출력 결과는 범주형 값

•

회귀: 데이터에 대한 수치를 예측하는 문제이며, 회귀 모델의 출력 결과는 연속형 값

•

활성화 함수의 사용: 일반적으로 분류에서는 소프트맥스(softmax), 회귀에서는 항등 함수를 활성화 함수로 사용

실습파일:

3_neural_networks.ipynb

59.43 KB • ipynb • https://drive.google.com

3.5.1 항등함수와 소프트맥스 함수 구현하기

항등 함수와 소프트맥스 함수 구현하기

•

항등 행렬(identity matrix): AI=AAI=AAI=A 또는 IA=AIA=AIA=A 를 만족하는 행렬 III를 행렬 AAA의 항등 행렬이라고 정의하며 모든 대각선 원소 값이 1이며 그 외의 원소 값은 0

◦

예: A=[123456],I=[100010001]A= \left[
\begin{matrix}
    1 & 2 & 3\\
    4 & 5 & 6\\
\end{matrix}
\right]
, I= \left[
\begin{matrix}
    1 & 0 & 0\\
    0 & 1 & 0\\
    0 & 0 & 1\\
\end{matrix}
\right]A=[14​25​36​],I=​100​010​001​​

AI= \left[ \begin{matrix} \color{blue}1\times 1 \color{gray}+ 2\times 0 + 3\times 0 & \color{gray}1\times 0 + \color{blue}2\times 1 \color{gray}+ 3\times 0 & \color{gray}1\times 0 + 2\times 0 + \color{blue}3\times 1\\ \color{blue}4\times 1 \color{gray}+ 5\times 0 + 6\times 0 & \color{gray}4\times 0 + \color{blue}5\times 1 \color{gray}+ 6\times 0 & \color{gray}4\times 0 + 5\times 0 + \color{blue}6\times 1\\ \end{matrix} \right] = \left[ \begin{matrix} 1 & 2 & 3\\ 4 & 5 & 6\\ \end{matrix} \right]

•

항등 함수(identity function): 모든 원소를 자기 자신으로 대응시키는 함수이며, 정의역과 공역이 같음

◦

집합 MMM이 주어졌을 때, 이에 대한 항등 함수는 idM:M→Mid_M: M\rightarrow MidM​:M→M 으로 정의되며, 원소 x∈Mx\in Mx∈M에 대해 idM(x)=xid_M(x)=xidM​(x)=x 를 만족

•

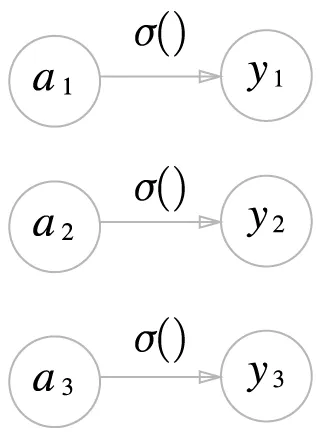
활성화 함수가 항등 함수일 경우: 입력 신호 = 출력 신호

항등 함수

•

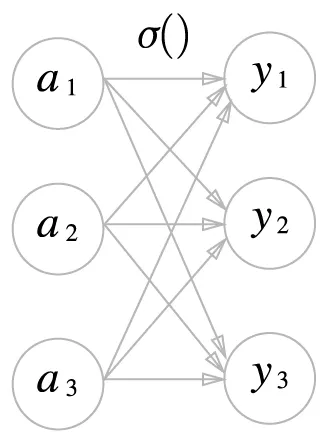
소프트맥스 함수(softmax function): 여러 개의 뉴런을 갖는 출력층에 적용되어 확률 값으로 변환하므로(모든 출력 값의 합 = 1) 다중 분류(multiclass classification)에 적합한 활성화 함수

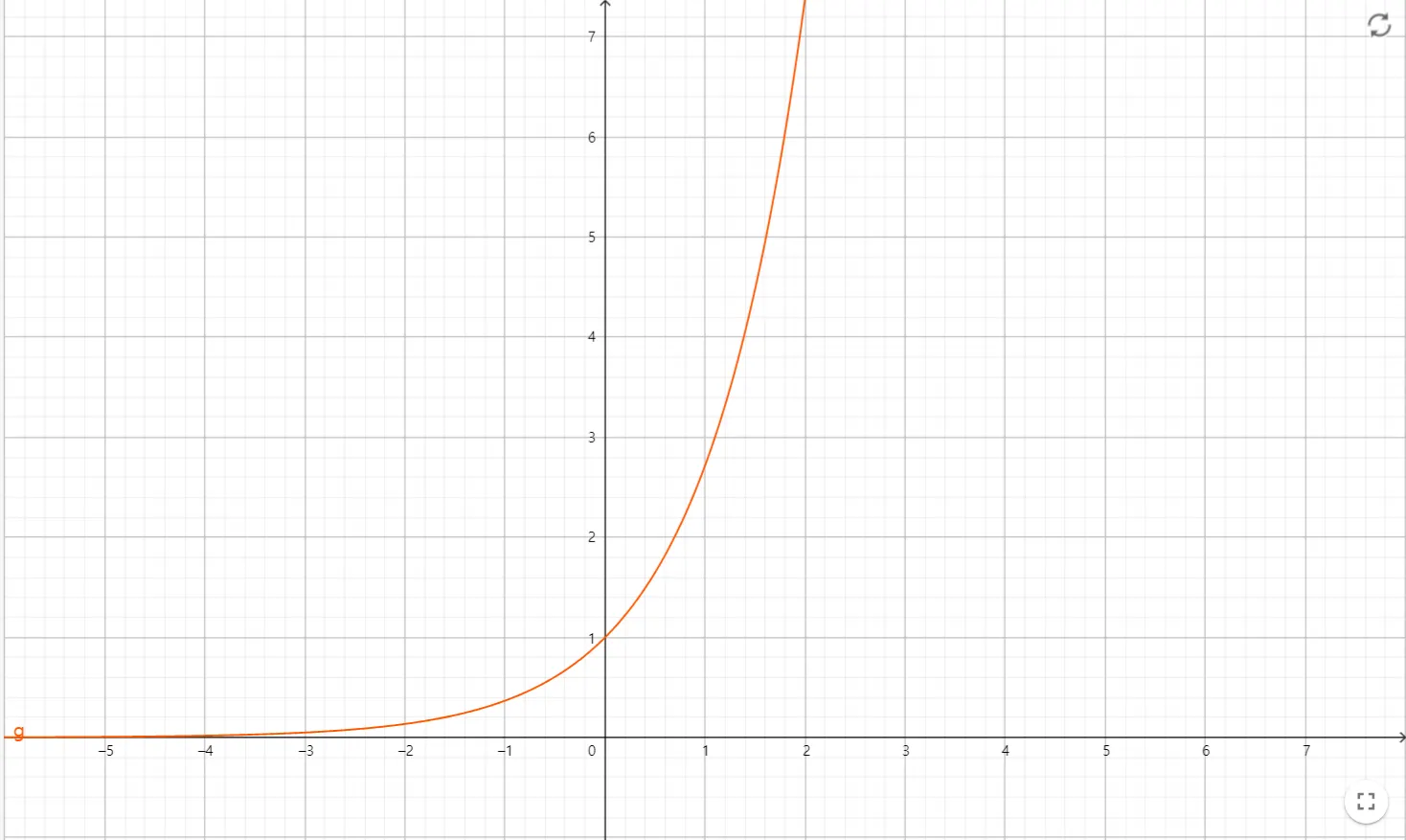
y_k=\frac{\text{exp}(a_k)}{\sum_{i=1}^{n}\text{exp}(a_i)}

◦

exp(x)\text{exp}(x)exp(x): Euler number (e≈2.718e\approx 2.718e≈2.718)의 지수 함수 (=ex=e^x=ex)

지수 함수

e^x

. 함수 값의 범위는 (0,

\infty

) 이다.

◦

nnn: 출력층의 뉴런 수

◦

yky_kyk​: kkk 번째 출력 값

◦

aka_kak​: kkk 번째 입력 신호

◦

소프트맥스 함수의 분자는 입력 신호 aka_kak​의 지수 함수 값( exp(ak)=eak\text{exp}(a_k)=e^{a_k}exp(ak​)=eak​)이며, 분모는 모든 입력 신호의 지수 함수 값의 합을 나타냄

◦

그러므로, ∑yk=1\sum{y_k}=1∑yk​=1 을 만족

소프트맥스 함수. 수식에 따라 각 출력은 모든 입력 신호와 연결된다.

•

소프트맥스에 eee가 사용되는 이유 

모든 입력에 대해 양수 값을 출력 (0,∞)(0, \infty)(0,∞) → 음수 및 zero division 방지 (어떠한 입력이 들어와도 안전하게 확률 값을 계산할 수 있음)

큰 값은 더 크게(중요도 ↑\uparrow↑), 작은 값은 더 작게(중요도 ↓\downarrow↓) 변환함

◦

예: 입력 신호 [0.3, 2.9, 4.0] 의 비중 = [0.042, 0.403, 0.556]
→ 소프트맥스 출력 값 = [0.018, 0.245, 0.737]

◦

단조 함수(monotonic function) 이므로 신호의 대소 관계는 변하지 않음

3.5.2 소프트맥스 함수 구현 시 주의점

◦

소프트맥스 함수: 지수항을 포함하므로, 입력 신호 값에 따라 값이 지수적으로 증가

▪

오버플로우(overflow) 문제: 데이터 타입의 값 범위를 넘어가는 경우가 발생

>>> np.exp(100)
2.6881171418161356e+43

>>> np.exp(1000)
inf
Python
복사
지수 함수의 오버플로우 문제

◦

오버플로우 문제 솔루션: 상수(CCC)를 이용한 트릭

y_k=\frac{\text{exp}(a_k)}{\sum^{n}_{i=1}\text{exp}(a_i)} = \frac{C\text{exp}(a_k)}{C\sum^{n}_{i=1}\text{exp}(a_i)} = \frac{\text{exp}(a_k+\text{log}C)}{\sum^{n}_{i=1}\text{exp}(a_i+\text{log}C)} =\frac{\text{exp}(a_k+C')}{\sum^{n}_{i=1}\text{exp}(a_i+C')}

▪

수식의 의미: 소프트맥스의 지수 함수를 계산할 때, 임의의 상수 CCC를 더하거나 빼도 결과는 동일

def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a-c) # a에 최대값을 빼서 오버플로우 방지
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a
    
    return y
JavaScript
복사

오버플로우를 방지하는 소프트맥스 함수 정의

3.5.3 소프트맥스 함수의 특징

◦

입력 신호에 대응되는 확률 값을 출력

◦

단조 함수이므로 값의 대소 관계가 바뀌지 않음

◦

기계학습 단계: 학습(모델 훈련) → 추론(모델 활용)

▪

학습 단계에서 소프트맥스 함수는 출력층의 예측 값을 확률 값으로 변환하며, 이는 확률 값을 기반으로 오차를 계산하는 크로스 엔트로피(cross entropy, 4장)와 결합되어 오차 역전파 과정으로 이어진다.

▪

반면에, 추론 단계에서 소프트맥스 함수는 불필요하므로(대소 관계 변경 X), 지수 계산에 드는 계산 비용을 방지하기 위해 생략되는 것이 일반적이다.

3.5.4 출력층의 뉴런 수 정하기

◦

출력층의 뉴런 수: 기계학습 문제에 맞게 결정 (예: 분류하고자 하는 클래스 수로 설정)

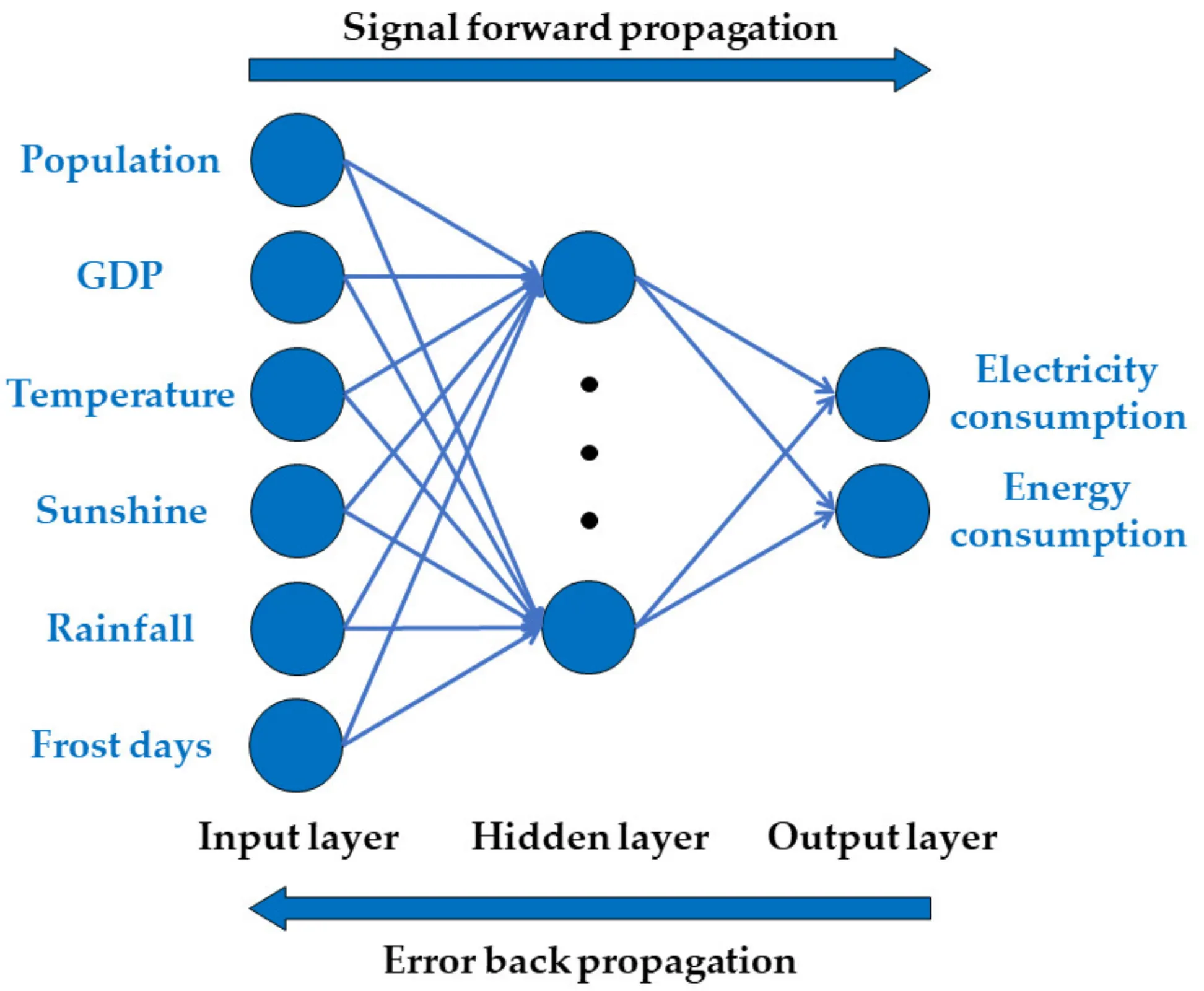
예: 다중 회귀(multiple regression)를 이용한 전력 및 에너지 소비 예측 문제 (Liu 2023, Processes)

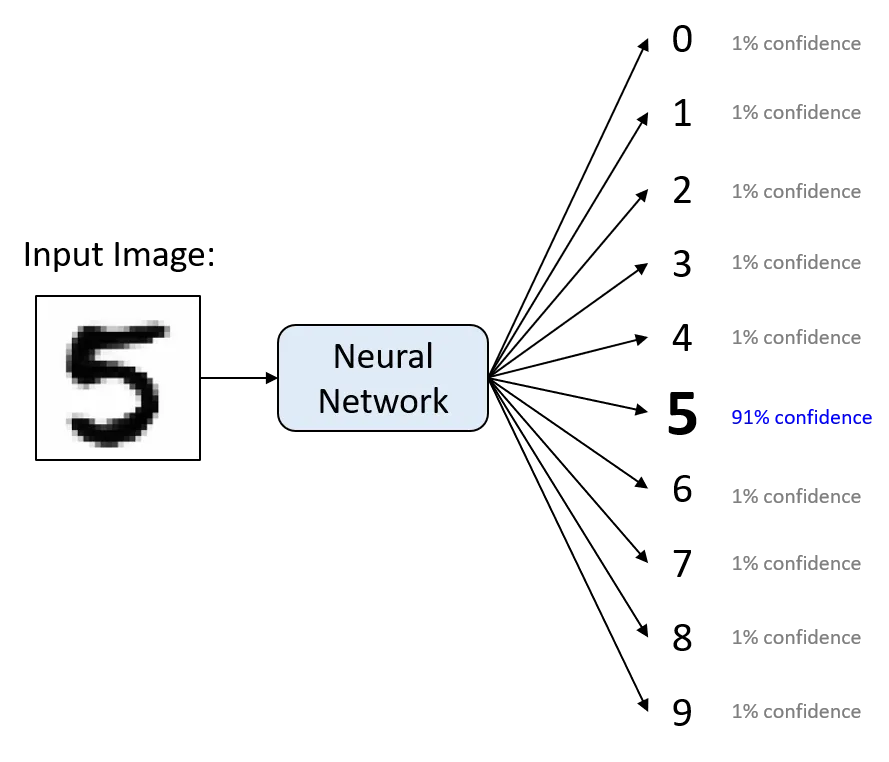
예: 숫자 필기(0-9) 분류 문제 (kaggle.com)

3.6 손글씨 숫자 인식

3.6.1 MNIST 데이터셋

•

MNIST (Mixed National Institute of Standards and Technology)

•

0부터 9까지의 손글씨 숫자 이미지 집합

•

훈련 이미지 60,000장, 시험 이미지 10,000장

•

훈련 이미지를 사용해 학습한 모델로 시험 이미지를 얼마나 정확하게 분류하는지 평가

•

28 * 28 크기의 회색조 이미지(channel=1), 각 픽셀은 0~255(픽셀의 밝기 값)의 값을 취함

•

각 이미지에 레이블 존재(‘7’, ‘2’, ‘1’)

•

라이브러리 및 데이터 불러오기

◦

common파일은 mnist 소스 코드 하단에 배치해야 함

import sys, os
sys.path.append(os.pardir)
import numpy as np
import pickle
from dataset.mnist import load_mnist
from common.functions import sigmoid, softmax

(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)
Python
복사

•

mnist 이미지 출력

from PIL import Image

def img_show(img):
    pil_img = Image.fromarray(np.uint8(img))
    pil_img.show()
    
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False)

img = x_train[0]
label = t_train[0]
img = img.reshape(28, 28) # 1차원 배열 이미지를 numpy array로 변환

img_show(img)
Python
복사

3.6.2 신경망의 추론 처리

•

입력층 뉴런 784개(28*28), 출력층 뉴런 10개(숫자 0~9)

•

은닉층 2개 (첫 번째 은닉층: 50개 뉴런, 두 번째 은닉층: 100개의  뉴런) → 뉴런 수 임의 설정

def get_data():
    (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
    return x_test, t_test

def init_network():
    with open("sample_weight.pkl", 'rb') as f:
        network = pickle.load(f)
        
    return network

def predict(network, x):
    
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']
    
    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = softmax(a3)
    
    return y
Python
복사

•

정확도 평가

x, t = get_data()
network = init_network()
accuracy_cnt = 0
for i in range(len(x)):
    y = predict(network, x[i])
    p = np.argmax(y) # 확률이 가장 높은 원소의 인덱스를 얻음
    if p == t[i]:
        accuracy_cnt += 1
        
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
Python
복사

3.6.3 배치 처리

•

Batch Processing 

: 데이터를 실시간이 아닌 일괄적으로 모아서 처리하는 작업

( Batch : 집단, 무리 한 회분, 일괄적인 처리를 위해 함께 묶다)

◦

일괄 작업 시스템(batch job system) 또는 일괄 처리 시스템(batch processing system)이라고 부름

◦

배치 처리 작업 중에 사용자와 상호작용이 불가능

◦

장점 : 성능 향상(병렬 처리), 메모리 효율성(배치 단위로 메모리에 올려 사용), 일반화 성능 향상(통계적 특정 반영) 등

◦

단점 : 작업 중간 결과 확인 불가, 메모리 요구량 증가(배치 크기가 클 때), 병렬화 문제(데이터 의존성 등), 배치 크기 수동 설정 등

•

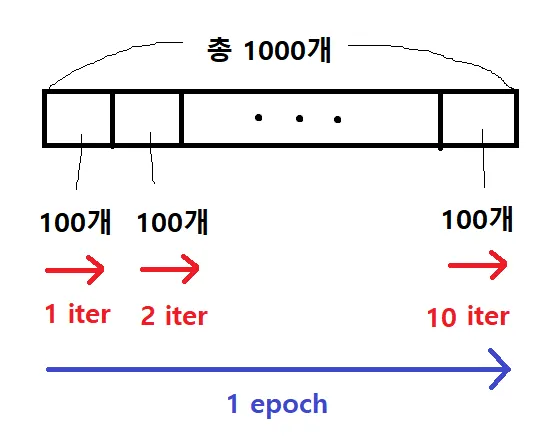
epoch: 전체 데이터셋에 대해 한 번 학습을 완료한 상태(1 epoch)

•

mini batch: 배치 처리 한 단계에 사용하는 작은 데이터 묶음

•

batch size: 하나의 mini batch에 넘겨주는 데이터 개수

•

iteration: 1 epoch을 마치는 데에 필요한 mini batch의 개수

•

배치 처리 구현

x, t = get_data()
network = init_network()

batch_size = 100 # 배치 크기
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])
    
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
Python
복사

3.7 정리

•

신경망에서는 활성화 함수로 시그모이드 함수와 ReLU 함수 같은 매끄럽게 변화하는 함수를 이용한다.

•

넘파이의 다차원 배열을 잘 사용하면 신경망을 효율적으로 구현할 수 있다.

•

기계학습 문제는 크게 회귀와 분류로 나눌 수 있다.

•

출력층의 활성화 함수로는 회귀에서는 주로 항등 함수를, 분류에서는 주로 소프트맥스 함수를 이용한다.

•

분류에서는 출력층의 뉴런 수를 분류하려는 클래스 수와 같게 설정한다.

•

입력 데이터를 묶은 것을 배치라 하며, 추론 처리를 이 배치 단위로 진행하면 결과를 훨씬 빠르게 얻을 수 있다.

손글씨(mnist) 분류 구현 코드

3_neural_network_mnist.zip

23140.2KB