DBSCAN

Density-Based Spatial Clustering of Applications with Noise

밀도 기반 클러스터링

정보통신학과 / 박사과정 4학기 / 오지연

1. 이론적 배경

1.1 정의

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)

•

1996년에 Martin Ester와 그의 동료들에 의해 제안된 밀도 기반 군집화 알고리즘으로, 
밀집된 데이터 포인트를 클러스터로 식별하고 밀도가 낮은 포인트는 노이즈로 간주함
특히 DBSCAN은 불규칙한 형태의 데이터 클러스터를 탐색하는 데 유용하며, 클러스터의 수를 미리 지정할 필요가 없다는 장점이 있음

•

머신 러닝에 주로 사용되는 클러스터링 알고리즘으로 Multi Dimension의 데이터를 밀도 기반으로 서로 가까운 데이터 포인트를 함께 그룹화하는 알고리즘

•

밀도가 다양하거나 모양이 불규칙한 클러스터가 있는 데이터와 같이 모양이 잘 정의되지 않은 데이터를 처리할 때 유용하게 사용 가능

1.2 주요 개념

밀도 기반 클러스터링

•

DBSCAN은 밀도가 높은 영역을 기반으로 군집을 형성, 데이터 분포의 밀도를 분석하여 포인트들이 얼마나 서로 가깝게 모여 있는지를 측정하고, 밀집된 영역을 클러스터로 정의

•

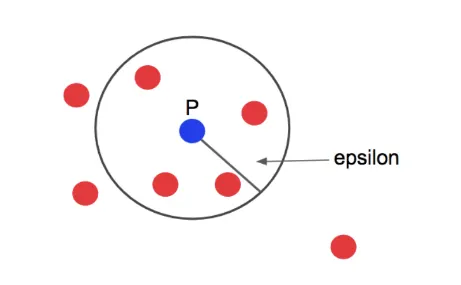
밀집 지역: eps(반경) 내에 일정한 수 이상의 포인트(min_samples, minPts)가 존재하는 지역을 의미

그림 출처 : https://bcho.tistory.com/1205

minPts = 4 라고 하면, 파란점 P를 중심으로 반경 epsilon 내에 점이 4개 이상 있으면 하나의 군집으로 판단할 수 있는데, 아래 그림은 점이 5개가 있기 때문에 하나의 군집으로 판단이 되고, P는 core point

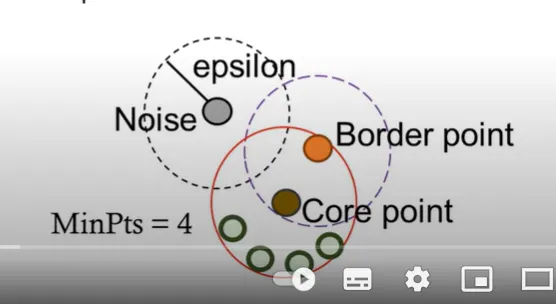
핵심 포인트(Core Point), 경계 포인트(Border Point), 노이즈 포인트(Noise Point)

•

핵심 포인트: 지정된 반경(eps) 내에 최소한의 포인트 수(min_samples)를 가진 포인트로, 클러스터 형성의 중심 역할을 함

•

경계 포인트: 반경 내에 min_samples에는 미치지 않지만, 핵심 포인트와 인접해 있어 클러스터에 포함되는 포인트

•

노이즈 포인트: 어느 클러스터에도 포함되지 않는 포인트로, 밀집되지 않은 외곽 영역의 포인트

그림 출처 : https://www.youtube.com/watch?v=OMO_atK0tVY

밀도 연결 및 밀도 도달성

•

밀도 연결(density-connected): 두 포인트가 서로 핵심 포인트를 통해 연결되어 클러스터를 형성할 수 있는 관계를 의미

•

밀도 도달성(density-reachable): 핵심 포인트에서 시작해 반경 내 다른 포인트로 이동하며 클러스터 내 모든 포인트에 도달할 수 있음

•

DBSCAN은 밀도가 높은 영역을 기반으로 군집을 형성합니다. 데이터 분포의 밀도를 분석하여 포인트들이 얼마나 서로 가깝게 모여 있는지를 측정하고, 밀집된 영역을 클러스터로 정의합니다.

•

밀집 지역: eps(반경) 내에 일정한 수 이상의 포인트(min_samples)가 존재하는 지역을 의미합니다.

1.3 주요 파라미터

•

DBSCAN의 두 가지 주요 파라미터는 eps와 min_samples

•

이 두 파라미터는 클러스터의 크기와 형태를 결정하는 중요한 요소

•

예를 들어, eps가 너무 작으면 작은 군집만 형성되고, 너무 크면 군집이 병합될 수 있음

•

min_samples가 클수록 더 강력한 군집을 형성하지만 노이즈로 분류되는 포인트가 증가할 수 있음

eps(epsilon)

•

포인트들이 서로 밀집되어 있다고 간주하기 위한 거리, 반경 eps 내에 특정 수 이상의 이웃이 있어야 밀집된 영역으로 간주

min_samples

•

하나의 클러스터로 인정하기 위해 eps 내에 있어야 할 최소한의 이웃 포인트 수

1.3 알고리즘 흐름

DBSCAN은 밀도가 낮은 지역을 쉽게 제외하고, 밀도가 높은 지역에서만 클러스터를 형성하는 방식으로 고정된 개수가 아닌 클러스터를 탐지할 수 있음

데이터셋에서 임의의 포인트를 선택

선택된 포인트가 핵심 포인트라면, 해당 포인트를 중심으로 반경 내에 있는 포인트들과 연결하여 클러스터를 형성

반경 내에 min_samples 이하의 포인트가 있으면 해당 포인트를 노이즈로 간주

연결된 모든 포인트가 클러스터로 묶일 때까지, 위 과정을 반복

1.4 장단점

DBSCAN은 고객 세분화, 이상치 탐지, 이미지 분석 등 다양한 분야에서 널리 활용

장점

•

불규칙한 모양의 클러스터: DBSCAN은 클러스터가 원형이 아니더라도 밀도에 따라 복잡한 모양의 클러스터를 찾는 데 유리

•

노이즈 처리: DBSCAN은 노이즈 데이터를 효과적으로 걸러내어 클러스터 내에 이상치가 포함되지 않도록 해야함

•

사전 클러스터 수 지정 불필요: DBSCAN은 k-means처럼 클러스터 수를 미리 지정할 필요가 없음

단점

•

밀도가 다양한 데이터에 약함: 밀도가 크게 차이나는 데이터에 대해선 성능이 떨어질 수 있음

•

eps와 min_samples 설정이 민감: 파라미터 설정에 따라 클러스터링 결과가 크게 달라질 수 있음

2. 동작 원리

DBSCAN의 동작 원리는 밀도 기반 접근 방식으로, 특정 지역의 밀집도를 기준으로 클러스터를 형성하는 것

2.1 기본 개념

DBSCAN은 데이터 포인트가 밀집된 영역을 클러스터로 정의하며, 이 과정에서 두 가지 주요 파라미터를 사용

eps

•

두 포인트가 같은 클러스터에 속하려면 이 정도 거리 이내에 있어야 하는 임계 반경

min_samples

•

한 포인트가 핵심 포인트로 간주되기 위해 eps 내에 포함되어야 할 최소 이웃 포인트 수

2.2 포인트의 유형

DBSCAN은 각 포인트를 다음 세 가지 유형으로 분류

핵심 포인트(Core Point)

•

eps 내에 min_samples 이상 이웃이 있는 포인트입니다. 이 포인트는 클러스터 형성의 중심이 됨

경계 포인트(Border Point)

•

eps 내에 min_samples 미만의 이웃이 있지만, 다른 핵심 포인트와 연결되어 있어 클러스터에 속할 수 있는 포인트

노이즈 포인트(Noise Point)

•

어느 클러스터에도 속하지 않는 포인트입니다. 밀도가 낮은 지역에 위치한 포인트로 간주

2.3 알고리즘 단계

임의 포인트 선택: 데이터셋에서 아직 방문하지 않은 임의의 포인트를 선택

이웃 포인트 탐색: 선택된 포인트를 기준으로 반경 eps 내에 있는 모든 이웃 포인트를 탐색하여, 이 포인트가 핵심 포인트인지 확인

•

이웃 포인트가 min_samples 이상 있으면 해당 포인트는 핵심 포인트로 간주

•

만약 이웃 포인트가 min_samples 미만이면 노이즈로 간주할 수도 있지만, 다른 핵심 포인트와 연결되면 경계 포인트가 될 수 있음

클러스터 확장: 핵심 포인트가 확인되면, 해당 포인트를 중심으로 이웃 포인트들을 클러스터에 추가. 이 과정에서 새롭게 추가된 이웃 포인트가 핵심 포인트일 경우, 이를 중심으로 추가적인 이웃 탐색을 통해 클러스터가 계속 확장됨

노이즈 포인트 구분: 클러스터에 속하지 않은 포인트는 노이즈로 간주 노이즈 포인트는 클러스터에 포함되지 않지만, 후속 클러스터 확장에서 경계 포인트로 변할 가능성도 있음

모든 포인트가 방문될 때까지 반복: 위 과정을 모든 포인트에 대해 반복하며, 더 이상 클러스터로 확장할 수 없는 경우 다음 클러스터 생성을 위해 새로운 미방문 포인트를 선택

2.4 DBSCAN의 강점 및 파라미터의 영향

DBSCAN은 클러스터 수를 미리 정의할 필요가 없고, 클러스터가 불규칙한 모양이어도 잘 찾아냄

하지만 eps와 min_samples 설정에 따라 결과가 크게 달라지므로 적절한 파라미터 튜닝이 필요

eps가 작으면 작은 클러스터가 여러 개 생기고, 크면 클러스터가 과도하게 확장될 수 있음

이러한 원리를 통해 DBSCAN은 고밀도 영역에서 클러스터를 형성하고, 밀도가 낮은 포인트는 노이즈로 분류하는 군집화 방법

3. 코드 구현 및 데모

Python의 scikit-learn 라이브러리는 DBSCAN을 쉽게 사용할 수 있는 기능을 제공

3.1 DBSCAN 알고리즘을 적용하여 클러스터링 결과를 시각화_코드 구현 예시

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.cluster import DBSCAN
from sklearn.preprocessing import StandardScaler

# 데이터셋 생성
X, y = make_moons(n_samples=300, noise=0.1, random_state=0)  # 반달 모양의 데이터셋 생성
X = StandardScaler().fit_transform(X)  # 데이터 표준화

# DBSCAN 모델 설정 및 학습
dbscan = DBSCAN(eps=0.3, min_samples=5)  # eps와 min_samples 설정
labels = dbscan.fit_predict(X)  # 모델을 통해 각 포인트의 클러스터 할당

# 결과 시각화
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=50, marker='o')
plt.xlabel("X-axis")
plt.ylabel("Y-axis")
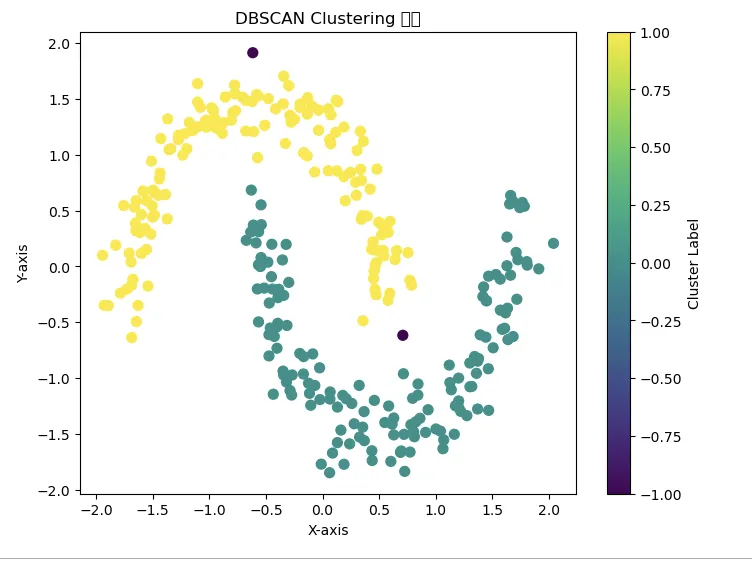
plt.title("DBSCAN Clustering 결과")
plt.colorbar(label="Cluster Label")
plt.show()
Python
복사

3.2 코드 설명

데이터 생성

•

make_moons 함수를 사용하여 반달 모양의 2D 데이터를 생성, 이 데이터는 불규칙한 형태의 클러스터로 이루어져 있어 DBSCAN을 사용하기에 적합

•

StandardScaler를 사용하여 데이터를 표준화하여 스케일 차이가 결과에 영향을 미치지 않도록 함

DBSCAN 모델 설정

•

DBSCAN 객체를 생성하고, eps=0.3과 min_samples=5로 설정

•

eps: 각 포인트에서 이웃 포인트를 찾는 반경(거리)

•

min_samples: 해당 반경 내에 있어야 하는 최소 이웃 포인트 수

모델 학습 및 클러스터 할당

•

fit_predict 메서드를 사용하여 DBSCAN 모델을 학습하고 각 포인트에 대해 클러스터 레이블을 할당

•

labels 변수에는 각 포인트가 속하는 클러스터 번호가 저장되며, 노이즈 포인트는 -1로 표시

결과 시각화

•

matplotlib를 사용하여 각 포인트의 클러스터를 시각화

•

포인트 색상은 클러스터 레이블에 따라 결정되며, 노이즈 포인트는 다른 색상으로 표시

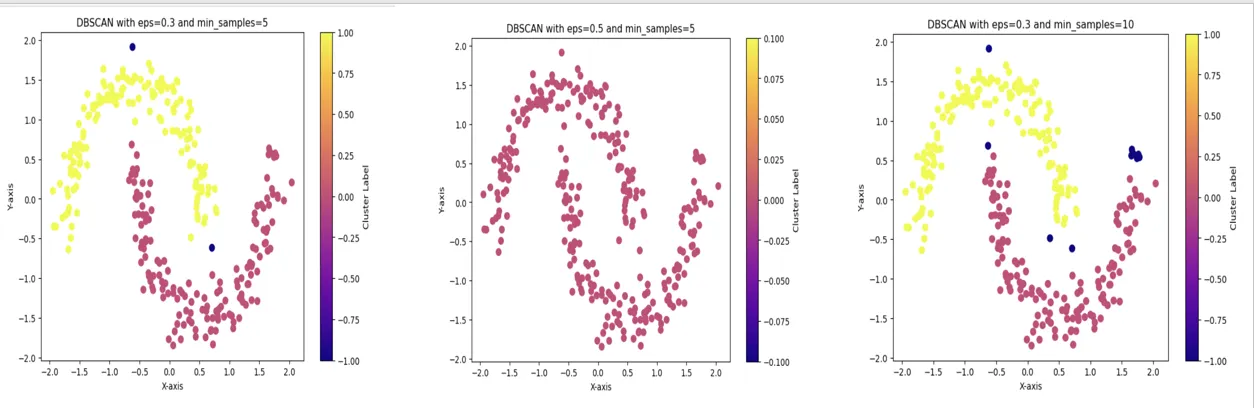
3.3 파라미터 변경에 따른 클러스터링 결과_코드 구현 예시

DBSCAN의 eps와 min_samples 값을 조정하면 결과가 크게 달라질 수 있음. 아래는 파라미터를 조정하며 결과를 비교할 수 있는 코드

# 파라미터 튜닝 실험 함수
def dbscan_experiment(eps_value, min_samples_value):
    # DBSCAN 모델 설정
    dbscan = DBSCAN(eps=eps_value, min_samples=min_samples_value)
    labels = dbscan.fit_predict(X)

    # 결과 시각화
    plt.figure(figsize=(8, 6))
    plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='plasma', s=50, marker='o')
    plt.xlabel("X-axis")
    plt.ylabel("Y-axis")
    plt.title(f"DBSCAN with eps={eps_value} and min_samples={min_samples_value}")
    plt.colorbar(label="Cluster Label")
    plt.show()

# 실행
dbscan_experiment(0.3, 5)  # eps=0.3, min_samples=5
dbscan_experiment(0.5, 5)  # eps=0.5, min_samples=5
dbscan_experiment(0.3, 10) # eps=0.3, min_samples=10
Python
복사

3.4 결과 분석

eps 값의 변화

•

eps가 작아지면 클러스터가 세밀해지지만 작은 군집이 여러 개 형성되고 노이즈로 분류되는 포인트가 증가

•

eps가 커지면 더 큰 영역을 포괄하는 클러스터가 형성되며, 적은 클러스터 수로 나뉠 수 있음

min_samples 값의 변화

•

min_samples 값이 커지면 클러스터에 포함되기 위한 최소 이웃 수가 증가하므로, 밀도가 높은 곳에서만 클러스터가 형성됨 그 결과로 노이즈가 많아질 수 있음

•

min_samples 값이 작아지면 더 많은 포인트가 클러스터로 포함되며, 노이즈가 줄어들 수 있음

이와 같이 파라미터 설정에 따라 클러스터링 결과가 달라질 수 있으므로, 실제 데이터에 맞는 적절한 파라미터 튜닝이 중요

3.5 결론

DBSCAN이 밀도가 높은 지역에서 클러스터를 형성하고 밀도가 낮은 포인트는 노이즈로 구분하는 방식으로 작동한다는 것을 확인할 수 있음

4. 번외

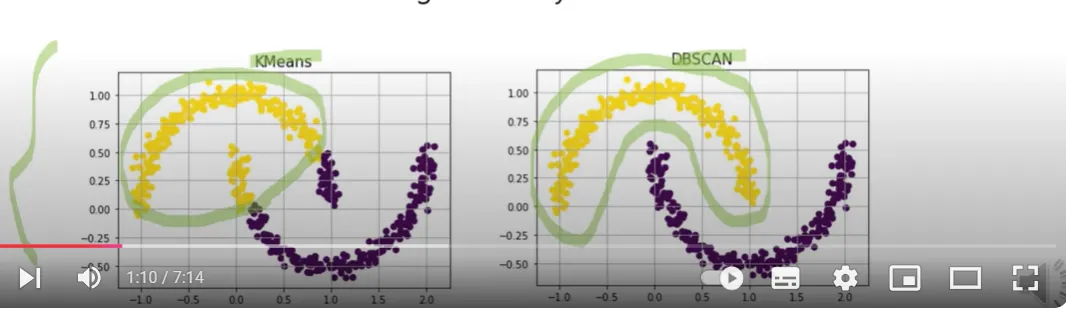
4.1 K-Means Clustering과의 차이

보통 Clustering 문제에서 K-Means Clustering을 우선 떠올리므로, K-Means Clustering과 DBSCAN의 차이 비

특징	DBSCAN	K-means Clustering
Cluster의 모양	데이터의 Cluster 모양이 arbitrary하게 묶이는 경우 잘 Clustering 됨	데이터의 Cluster 모양이 Spherical한 경우에 잘 Clustering 됨
Cluster의 개수	군집화 개수를 미리 정해주지 않아도 됨(밀도 기반)	군집화 될 개수를 미리 정해줘야함 (centroid 기반)
Outlier	Clustering에 포함되지 않는 Outlier를 특정할 수 있음	모든 데이터가 하나의 Cluster에 포함됨
Initial Setting	초기 Cluster 상태가 존재하지 않음	초기 Centroid 설정에 따라 결과가 많이 달라짐

•

DBSCAN과 K-means Clustering 사이에 어느 것이 좋다는 다루는 데이터에 따라 많이 달라짐

•

DBSCAN은 일반적으로 K-means Clustering에 비해 <불규칙 데이터를 다룰 때,  Noise와 Outlier가 많을 것으로 예상될 때, 데이터에 대한 사전 예측이 어려울 때> 활용하는 것이 좋다.

•

DBSCAN은 K-means Clustering에 비해 <Computational Cost가 많이 든다는 점, 예측과 해석이 어렵다는 점>의 단점이 있다.

그림 출처 : https://www.youtube.com/watch?v=OMO_atK0tVY

참고 자료

DBSCAN의 창시 논문

•

Martin Ester, Hans-Peter Kriegel, Jörg Sander, Xiaowei Xu가 발표한 "A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise" 논문리뷰를 참고하여 알고리즘의 기본 개념과 동작 원리 등을 설명

기계 학습 및 데이터 마이닝 기본서

•

"Pattern Recognition and Machine Learning" (Christopher M. Bishop): 클러스터링과 밀도 기반 군집화에 대한 이론적 배경 리뷰 참고

•

"Data Mining: Concepts and Techniques" (Jiawei Han, Micheline Kamber, Jian Pei): 클러스터링 알고리즘, 특히 밀도 기반 클러스터링에 대한 자세한 개념 설명 리뷰 참고

YouTube

•

https://www.youtube.com/watch?v=OMO_atK0tVY

•

https://www.youtube.com/watch?v=OMO_atK0tVY