Search

Probability Distribution (확률분포)

@Hyun Ahn @8/9/2023
사건(event)에 대한 확률이 어떻게 분포되어 있는지를 나타내는 정보이다. 사건의 특성(이산형 or 연속형)에 따라 확률분포를 확률질량함수, 누적분포함수, 확률밀도함수 등의 형태로 정의할 수 있다.

확률변수

확률 변수(random variable)는 발생 가능한 모든 사건에 실수 값(xx)을 할당하는 함수 XX이다. 확률 변수에 할당된 모든 값에 해당되는 사건이 발생할 가능성을 나타내는 정보가 확률분포이다. 예를 들어, 동전을 던지는 실험을 시행해서 나올 수 있는 결과는 앞면(head)과 뒷면(tail)이 있으며, 이를 확률 변수로 표현하면 각각 X(head)=0,X(head)=0, X(tail)=1X(tail)=1과 같이 나타낼 수 있다.
이러한 확률변수는 번호를 붙여 ‘셀 수 있는가(countable)’의 기준에 따라 이산확률변수와 연속확률변수로 구분된다.
•
이산확률변수: 확률변수의 값들을 셀 수 있는 경우
◦
예: 정수 집합, {−2,−1,0,1,2,...}\{-2,-1,0,1,2,...\}
•
연속확률변수: 확률변수의 값들을 셀 수 없는 경우
◦
예: 실수 집합, {x∣1≤x≤3}\{x|1\leq x \leq 3\}. 1.01.0과 1.11.1사이에는 무한히 많은 실수들이 존재한다(실수의 완비성). 그러므로, 범위가 주어진 실수 집합에는 ‘몇 번째 실수’ 라는 개념이 성립되지 않기 때문에 셀 수 없는 존재이다.

이산확률변수

이산확률변수(discrete random variable) XX에 대한 확률분포는 확률질량함수(probability mass function, pmf)로 나타낸다. 이는 이산확률변수 XX에 대해 특정 사건(X=xX=x)이 일어날 확률을 대응하는 함수이다.
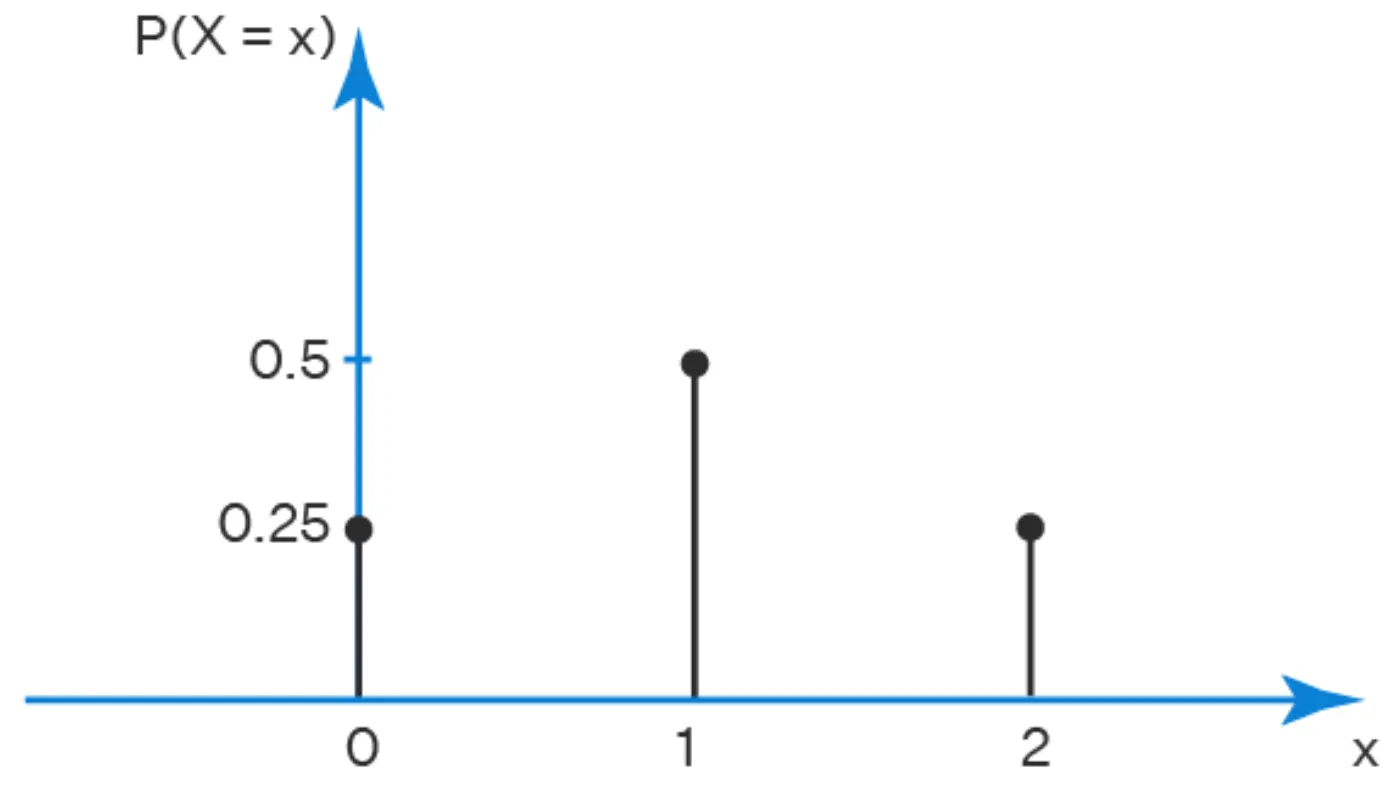
나는 가위바위보 놀이를 할 때, 나의 성향에 따라 가위는 25%, 바위는 50%, 그리고 보는 25% 의 확률로 선택한다.
위의 예시를 확률변수 X(가위)=0,X(바위)=1,X(보)=2X(\text{가위})=0, X(\text{바위})=1, X(\text{보})=2 와 같이 나타내며, 각각의 사건에 대한 확률은 P(X=0)=0.25,P(X=1)=0.5,P(X=2)=0.25P(X=0)=0.25, P(X=1)=0.5, P(X=2)=0.25 이다.
확률변수 XX에 대한 확률질량함수는 pX(x)p_{X}(x)와 같이 표현하며 위의 예시에 적용하면 pX(0)=0.25,pX(1)=0.5,pX(2)=0.25p_{X}(0)=0.25, p_{X}(1)=0.5, p_{X}(2)=0.25 와 같이 표현된다.
가위바위보에 대한 확률질량함수 (출처: Cuemath)

연속확률변수

이산확률변수와는 다르게 연속확률변수(continuous random variable)에서는 확률변수의 값들이 무한히 많고 셀 수 없으므로, 특정 사건에 대한 확률 P(X=x)P(X=x)을 정의할 수 없다. 대신에 누적분포함수 또는 확률밀도함수를 통해 확률변수 값이 특정 범위 내에 있을 확률을 계산할 수 있다.
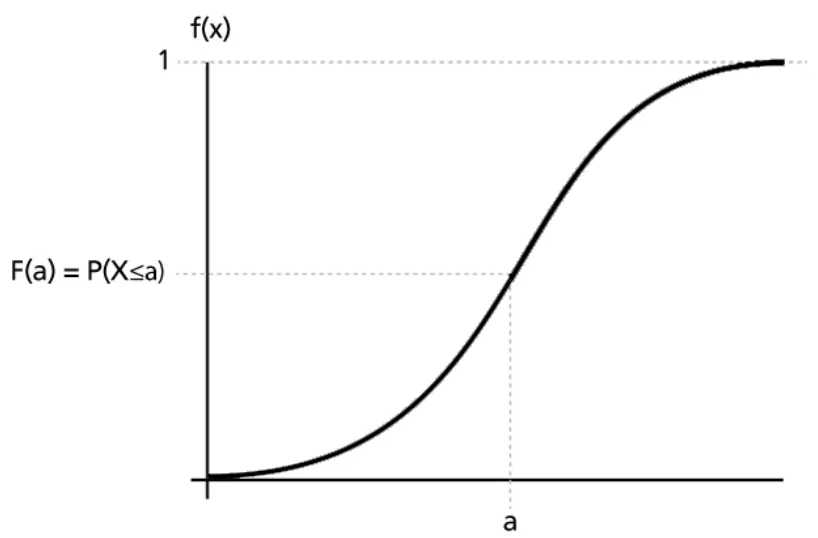
누적분포함수(cumulative distribution function, cdf)는 확률변수 XX가 특정 값 xx 이하가 될 확률을 나타낸다.
F(x)=P(X≤x)F(x)=P(X\leq x)
연속확률변수 X가 a 이하일 확률을 표현하는 누적분포함수 (출처: Reliawiki)
누적분포함수는 이산확률변수와 연속확률변수 모두 적용가능하다. 그러나, 특정 값 이하에 대한 확률을 구할 때 용이한 반면에, 전반적인 확률 분포의 형상을 파악하기 어려운 점이 있다.
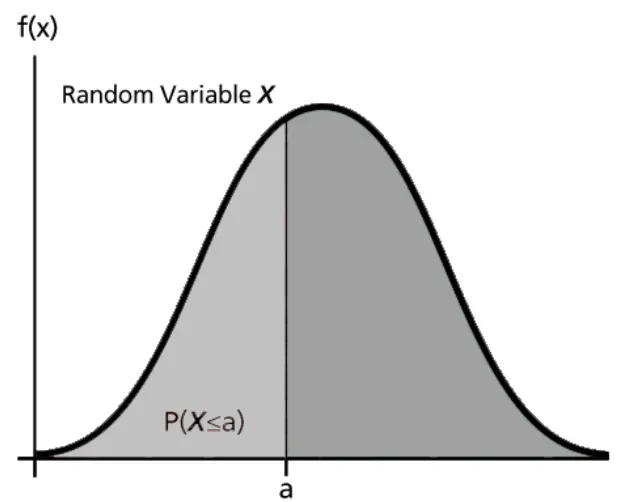
반면에, 확률밀도함수(probability density function, pdf)는 연속확률변수의 확률분포를 누적분포함수보다 더 직관적으로 표현하며 수학적으로는 누적분포함수의 도함수(derivative)로 정의된다.
f(x)=ddxF(x)f(x)=\frac{d}{dx}F(x)
위의 누적분포함수를 나타내는 확률밀도함수
반대로, 확률밀도함수의 적분을 통해 특정 값 xx에 대한 누적분포함수도 구해진다.
F(x)=P(X≤x)=∫0xf(s)dsF(x)=P(X\leq x)=\int_{0}^{x}f(s)ds
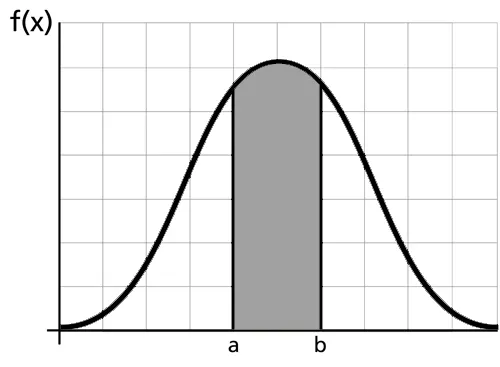
누적분포함수와는 다르게 확률밀도함수에서는 적분을 통해 임의의 구간 [a,b][a, b]에 대한 확률을 구할 수 있다.
P(a≤X≤b)=∫abf(x)dxP(a\leq X \leq b)=\int_{a}^{b}f(x)dx
임의의 구간에 대한 확률밀도함수
표본공간 전체(−∞,+∞)(-\infty, +\infty)에 대한 확률밀도함수의 면적은 항상 11을 만족한다.
∫−∞+∞f(x)dx=1\int_{-\infty}^{+\infty}f(x)dx=1
위와 같이 누적분포함수와 확률밀도함수는 특정 값에 대한 확률을 의미하지 않고, 연속확률변수의 특정 범위에 대한 확률을 구할 때 사용될 수 있다.

참고 자료

•
Basic Statistical Background, ReliaWiki (link)
•
통계의 본질, 이산 vs 연속확률변수 (1) 구별 방법, 티스토리 (link)
•
확률밀도함수는 확률이 아니다?, 성균관대 수학과 (link)
•
확률분포함수, 데이터 사이언스 스쿨 (link)
Made with