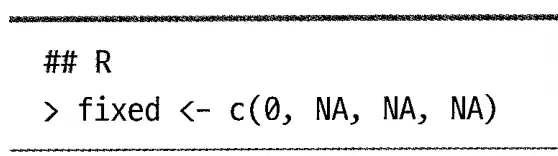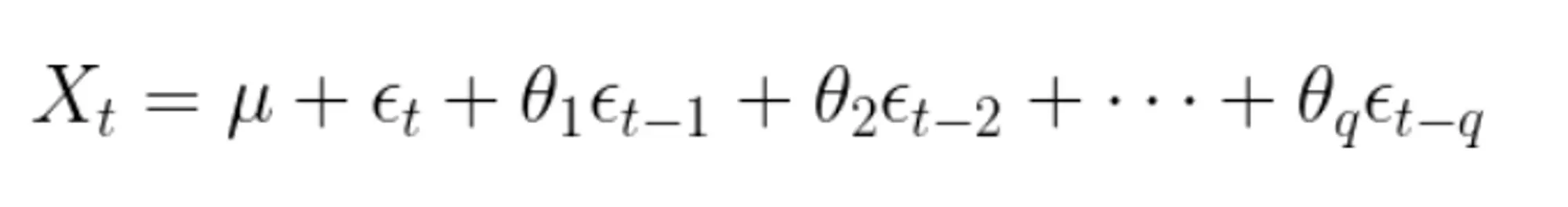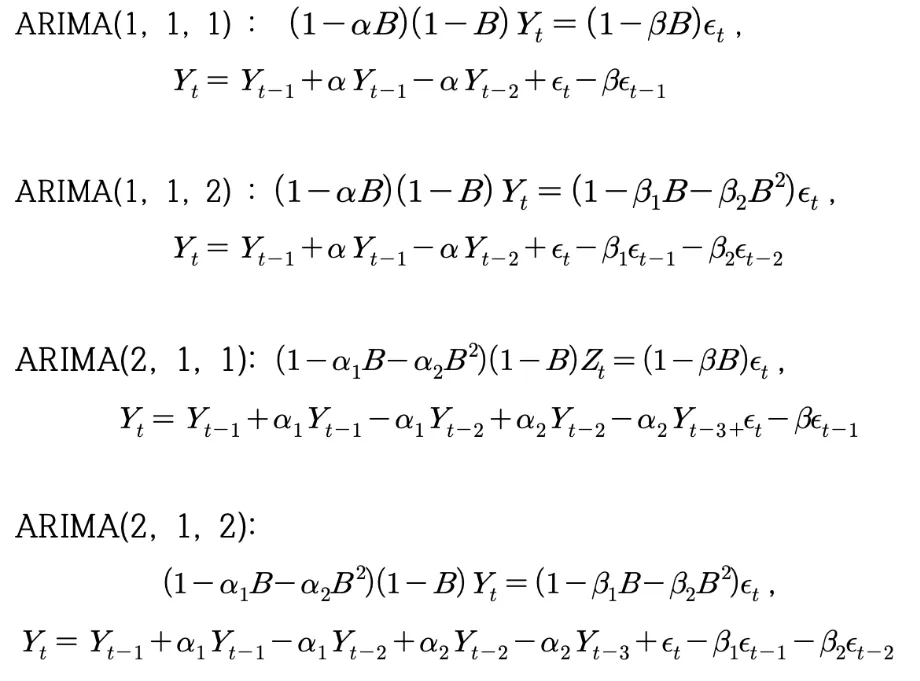6️⃣

시계열의 통계 모델

•

시계열에 대한 몇가지 선형적인 통계모델들 

→같은 시계열 내 데이터 간 발생하는 상관관계 정보 제공

◦

자기회귀autoregressive(AR) 모델  

◦

이동평균moving average(MA) 모델 

◦

자기회귀누적이동평균autoregressive integrated moving average(ARIMA)모델 

◦

벡터자기회귀vector autoregressive(VAR) 

◦

계층형hierarchical 모델 

6.1 선형회귀를 사용하지 않는 이유

•

시계열 데이터에는 통상적으로 회귀모델 사용하지 않음

◦

선형 회귀 분석의 가정인 독립항등분포 Independently and Identically Distributed(IID) 조건이 시계열 데이터에서는 성립하지 않는 경우가 대부분

◦

데이터는 그 시간 step에 영향이 클수록 시간과 강한 상관관계를 가짐
위 가정이 성립되지 않아 선형 회귀 쓰는 것이 바람직하지 않음 

독립항등분포 : 동일한 모집단에서 독립적인 추출을 시행. 확률변수가 여러 개 있을 때 (X1 , X2 , ... , Xn) 이들이 상호독립적이며, 모두 동일한 확률분포 f(x)를 가진다

자기상관Autocorrelation

이전 시간 단계의 값이 현재 값에 영향을 줄수 있고, 이는 자기상관 구조를 만들어냄

선형회귀 모델은 이러한 자기상관을 고려하지 않기때문에 시계열 데이터에 적합하지 않음

비정상성Non-stationarity

시계열 데이터는 시간에 따라 평균, 분산 또는 자기상관 구조가 일정하지 않을 수 있음

이런경우 선형회귀 모델의 가정이 깨지며 모델의 예측력이 크게 저하됨

계절성과 트랜드Seasonality and Trend

시계열 데이터는 계절성과 트랜드 포함

이런 패턴은 선형회귀모델로 충분히 설명하기 어려움

비선형성Non-linearity

시계열 데이터는 종종 비선형적인 패턴을 보일수 있음

선형회귀 모델은 비선형성을 적절히 모델링하지 못함

•

다음과 같은 조건 충족시 최소제곱선형회귀least squares linear regression모델을 시계열 데이터에 적용 가능

◦

시계열의 행동에 대한 가정 

▪

시계열은 예측 변수에 대한 선형적 반응 보임 

▪

입력 변수는 시간에 따라 일정하지 않거나, 다른 입력 변수와 완벽한 상관관계를 갖지 앉음 

◦

오차에 대한 가정 

▪

각 시점 데이터에 대해 모든 앞뒤 시기의 설명변수에 대한 예상 오차값은 0 

▪

특정 시기의 오차는 과거나 미래의 모든 시기에 대한 입력과 관련 없음.
오차에 대한 자기상관 함수 그래프는 어떤 패턴도 띄지 않음 

▪

오차의 분산은 시간으로부터 독립적 

•

위의 가정이 성립된다면 보통최소제곱회귀ordinary least squares regression는 주어진 입력에 대한 계수의 비편향추정량unbiased estimator이 되며 이는 시계열 데이터에서도 마찬가지임 

보통최소제곱회귀OLS

비편향추정량이란

6.2 시계열을 위해 개발된 통계 모델

6.2.1 자기회귀모델

•

자기회귀autoregressive, (AR) 모델은 과거가 미래를 예측한다는 직관적인 사실에 의존함  

•

특정 시점 t의 값은 이전 시점들을 구성하는 값들의 함수라는 시계열 과정을 상정함

AR(AutoRegressive)

대수학을 활용한 AR 처리 과정의 제약 사항 이해

•

자기회귀는 과거 값들에 대한 회귀로 미래 값을 예측하는 방식임

•

간단한 AR 모델예시

AR(1):

y_t = b_0 + b_1 *y_{t-1}+e_t

•

시간 t에서 계열의 값은 상수b0b_0b0​ 

•

이전 시간 단계에서 값에 상수를 곱한 b1∗yt−1b_1*y_{t-1}b1​∗yt−1​ 

•

시간에 따라 달라지는 오차항 ete_tet​에 대한 함수는 일정한 분산 및 평균 0을 가진다고 가정 

•

 자기회귀라는 용어는 직전 시간만 되돌아보는 AR(1)을 얘기함  

•

AR(1)모델은 하나의 원인 변수만 지닌 간단한 선형회귀 모델과 동일한 형식

Y=b_0+b_1*x+e

와 매핑됨

•

b0,b1b_0,b_1b0​,b1​값을 알고 있다면, 주어진 yt−1y_{t-1}yt−1​ 조건에서의 yty_tyt​의 기대값 분산 모두 계산 가능 

식6-1

E(y_t|y_{t-1})=b_0+b_1*y_{t-1}+e_t

Var(y_t|y_{t-1})=Var(e_t)=Var(e)

•

AR() 표기를 일반화 할때 p를 사용할 수 있음 

⇒ AR(p)라고 식을 일반화할 수 있음, p는 가장 최근 값들의 개수를 의미함

•

전통적인 표기법

◦

여기서 사용된 ϕ는 자기회기계수 auto regression coefficient를 나타냄

자기회기계수

y_t=ϕ_0+ϕ_1*y_{t-1}+ϕ_2*y_{t-2}+...+ϕ_p*y_{t-p}+e_t

•

시계열 분석의 가장 핵심은 정상성임 

•

정상성은 AR 모델을 포함한 많은 시계열 모델에서 기본적으로 가정 :

시계열의 평균, 분산, 공분산과 같은 통계적 속성이 시간이 지남에 따라

변화하지 않는 것

AR 모델의 다양한 형태

AR(p) 모델의 파라미터 선택

•

데이터가 AR 모델 적합한지 평가시

◦

과정과 편자기상관함수partial autocorrelation function, PACF 그래프 이용

•

AR과정의 PACF는

◦

차수 p를 넘는 부분을 0으로 잘라버림

◦

그 결과 데이터에서 실증적으로 볼 수 있는 AR 과정 차수를 구체적이며 시각적으로 표시

◦

AR 과정은 시간의 위치가 증가(미래)할수록 지수적으로 완화됨을 의미하는 자기상관함수(ACF)의 형태를 갖지만 유의미한 ACF는 아님 

⇒ 이를 통해, 0으로 잘라버리기 직전의 p를 확인하여 유의미한 차수를 결정

ACF

PACF

•

실습 

◦

사용 데이터 UCI 머신러닝 저장소에 게시된 수요 예측 데이터(https://perma.cc/B7EQ-DNLU)  

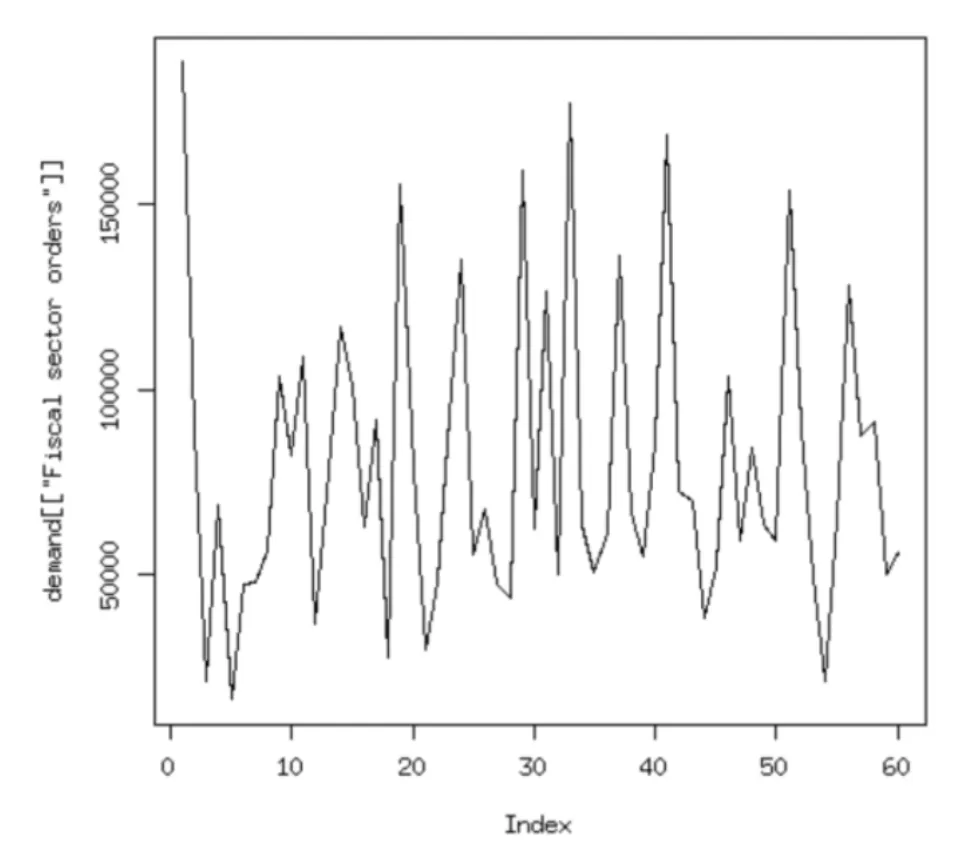
그림6-1 은행의 일일 주문 건수(2)

◦

시간 순대로 데이터의 그래프를 그림 

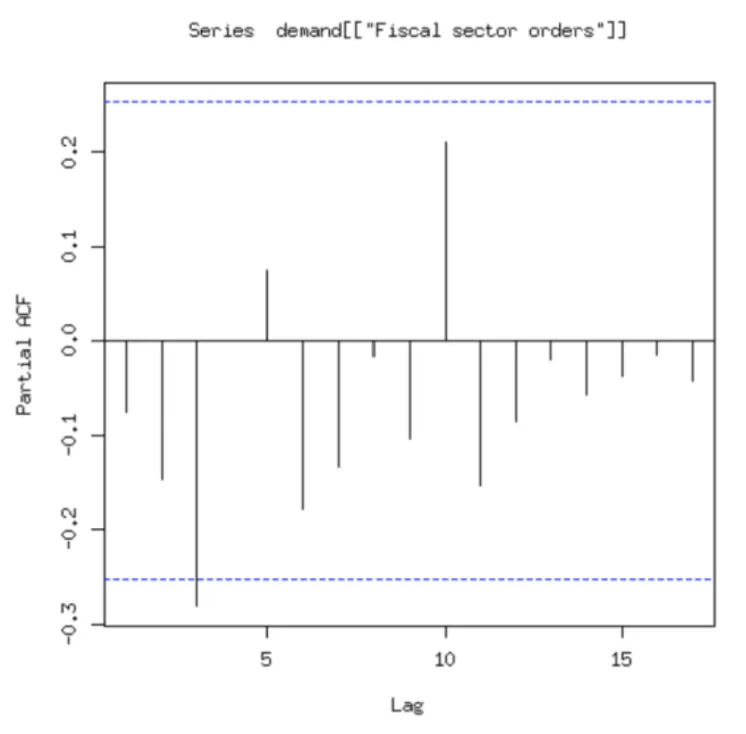
그림6-2 [그림6-1]에서 묘사된 가공되지 않은 차수의 시계열에 대한 PCAF

◦

위의 데이터를 AR과정으로 모델링하기 위해 PACF로 AR 과정의 시차를 잘라냄 

◦

lag 3의 값이 임계값 5%를 초과

◦

R의 stats 패키지가 제공하는 ar()함수 결과와 일치

◦

파라미터값 지정하지 않은 경우 ar()함수는 자동으로 자기회귀모델 차수 선택  

◦

ar()함수에서 선택된 차수는 아카이케 정보기준AIC에 따라 결정 

◦

아카이케 정보기준은 PACF의 시각적 선택과 정보기준의 최소화로 얻은 선택이 일관성을 보여주기 때문에 유용함 

아카이케 정보기준 

◦

차수 파라미터를 (3,0,0)으로 설정 AR(3)을 적합하는 함수의 호출방법 (3은 AR 요소의 차수)

◦

order = c(3,0,0) : ARIMA 모델 차수 지정
AR(3) 모델 적합위해 (p,d,q)=(3,0,0) 설정
p는 AR 모델의 차수, d는 차분의 차수, q는 MA 모델의 차수를 나타냄 

◦

계수를 0으로 제한, 지연-1항을 0으로 유지시

◦

fixed =c(0,NA,NA,NA) : 고정할 계수 설정
첫번째 시점의 영향을 배제(첫번째 지연항 0으로 고정)하고 모델을 적합함 

◦

arima함수의 fixed 파라미터 벡터값에 NA 대신 0 삽입

◦

이전 시전값의 영향을 받지 않도록, 데이터가 자기상관 구조를 가지지않는 경우, 모델을 간단히 유지하고자 할때 유용함 

•

모델의 적합도 검정 : ACF 그래프  / 륭-박스 검정

•

ACF 그래프

◦

모델의 잔차(오차)에 대한 ACF 그래프 : 자체상관 패턴 유무 확인 방법 

◦

acf()사용 잔차그래프 그리기

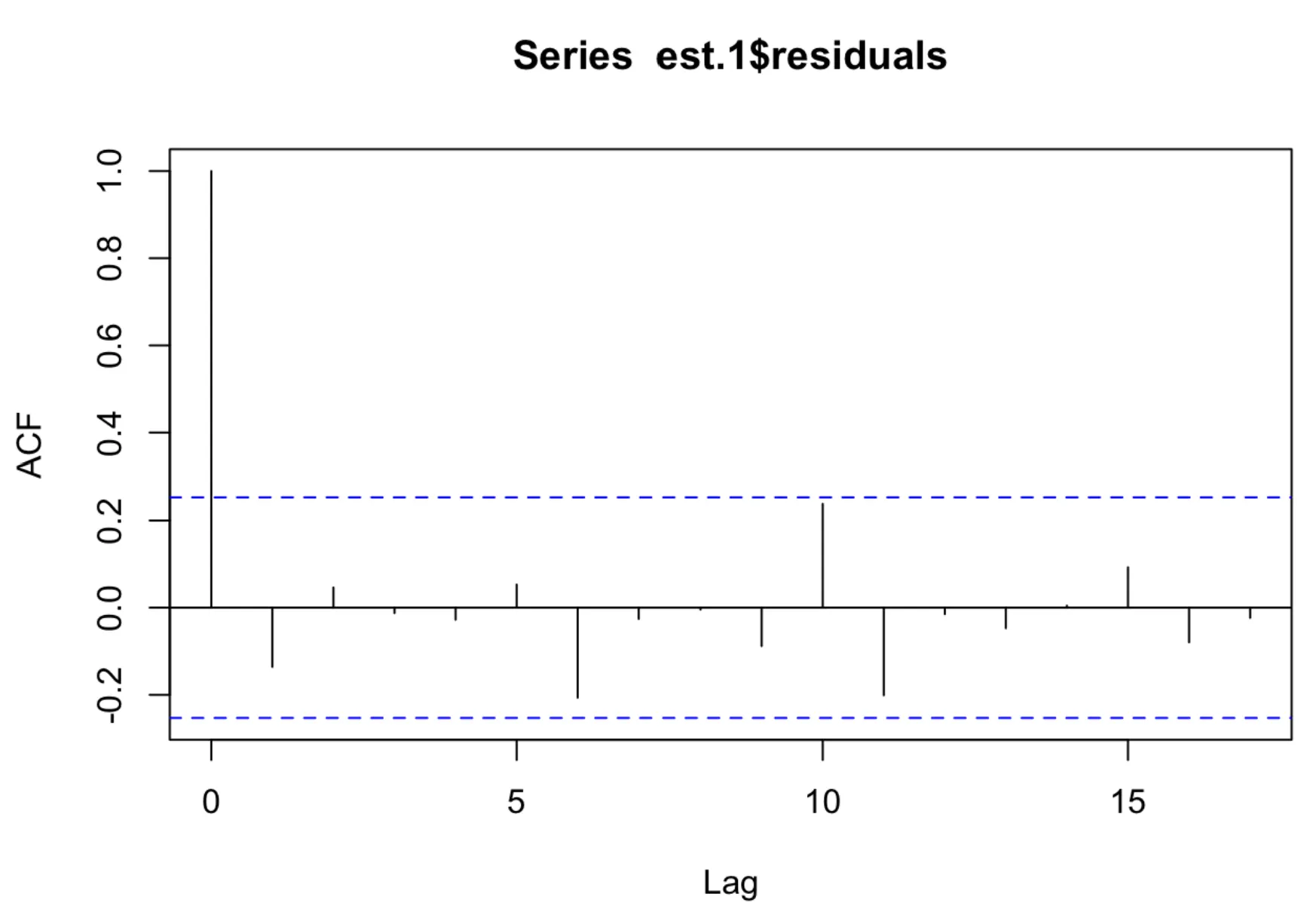
그림 6-3 지연 -1 파라미터를 0으로 강제하여 적합시킨 AR(3)모델의 잔차에 대한 ACF

▪

ACF값 중 어느것도 임계값을 넘기지 않음(유의미) 

▪

이 그래프로는 잔차들간의 자체상관 패턴을 찾아볼 수 없음 

•

륭-박스 검정 

◦

시계열의 임의성을 검정하는 방법으로 귀무과설과 대립가설 검정함 

◦

H0 : 데이터가 일련의 상관관계를 나타내지 않는다

◦

H1 : 데이터가 일련의 상관관계를 나타낸다 

◦

이 검정은 AR보다 ARIMA 모델 적용이 일반적, 적합한 모델의 잔차에 적용됨 

륭-박스 검정을 est.1 모델에 적용, 모델 적합도 평가

◦

p-value의 값 0.05 이상, 귀무가설 기각할 수 없음, 잔차의 그래프 사실 확정 

정상성 검증

AR(p) 과정으로 예측하기

시간을 한단계 앞서 예측하기

•

AR모델로 시간을 한단계 앞서 예측하는 상황 고려, 지연 -1의 계수가 0으로 제한된 demand 데이터에 대한 모델로 작업 진행 

◦

forecast 패키지 fitted()함수 이용한 코드와 예측 그래프 

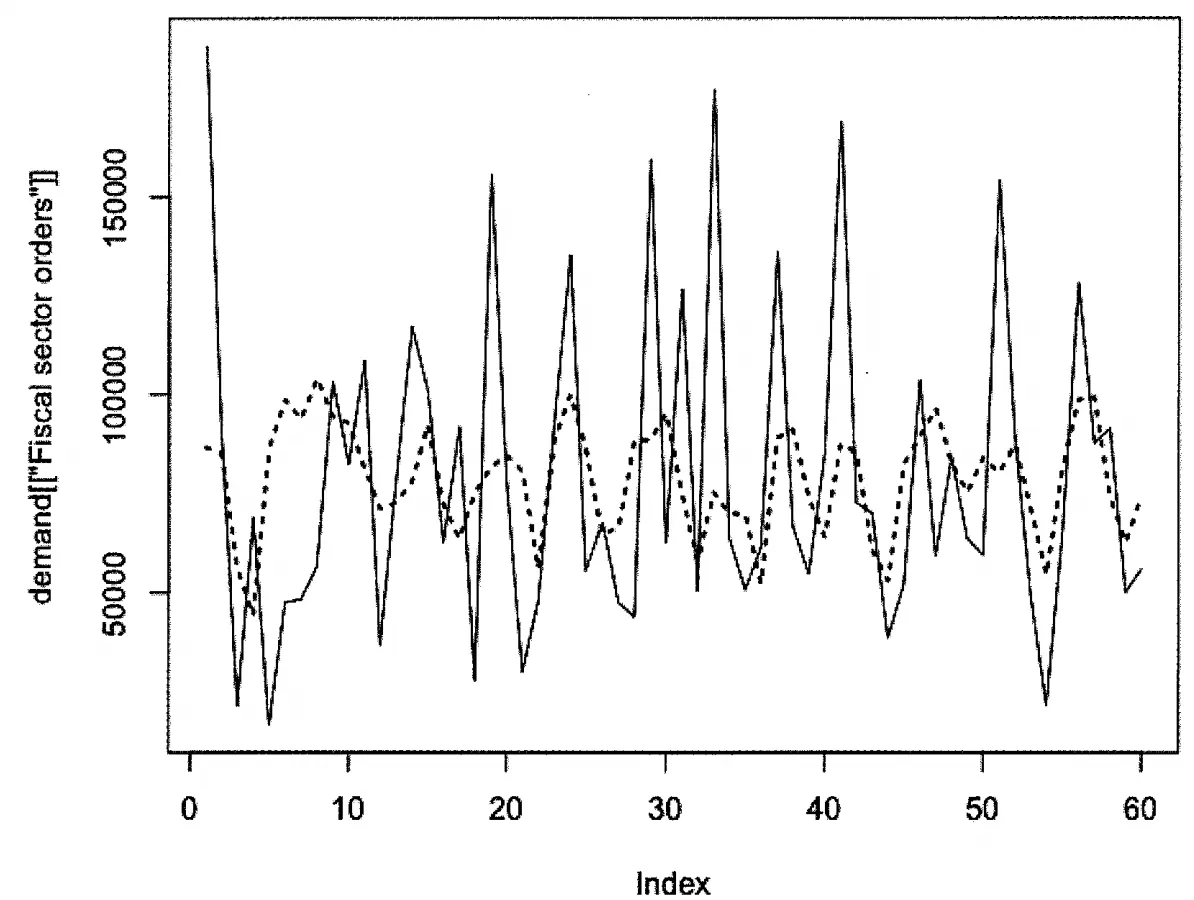
그림6-4 실선은 원본 시계열, 파선은 적합된 시계열

AR(p) 모델은 이동윈도함수(moving window function) 

•

예측의 품질 

◦

원본데이터의 계열과 예측 모두에 대한 차분을 구해서 비교 

◦

차분을 구한 다음 예측과 데이터가 유사한 패턴 보이면 모델이 의미 있다고 판단 (그림6-5) 

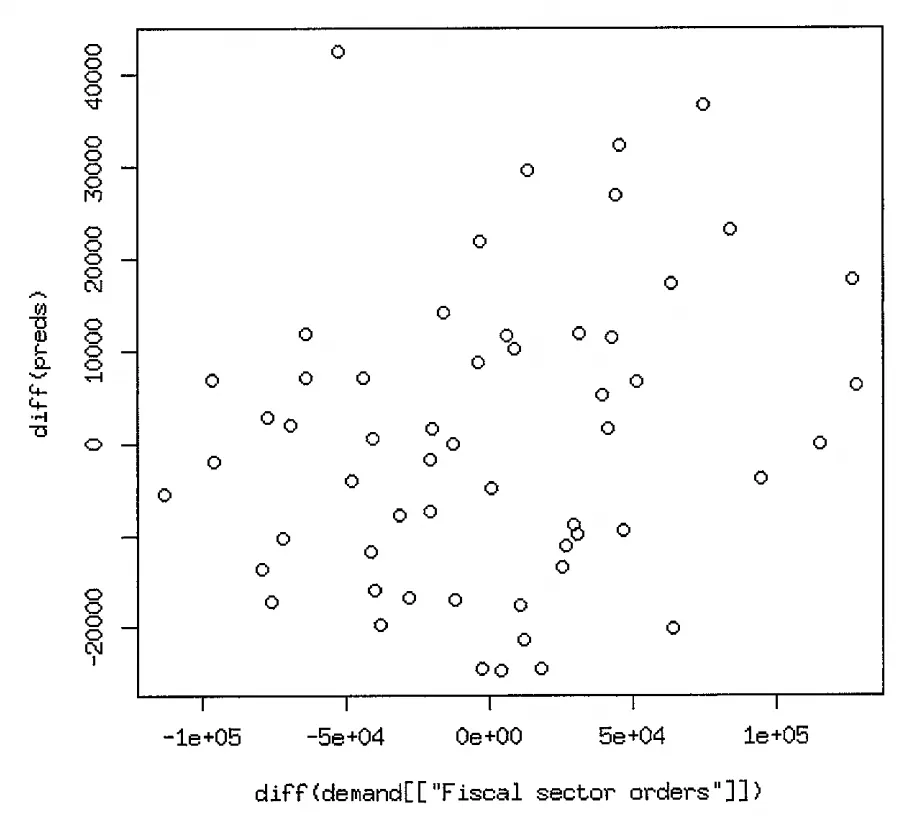
그림6-5 원본 계열 및 예측의 차분 사이에는 강한 상관관계가 있으며 이는 모델이 실제로 근본적인 관계를 식별할 수 있음을 시사함

◦

원본 계열의 차분 그래프로 상관관계 살펴보는 것으로 동일 시기 동일한 움직임 예측 여부 검정 

◦

예측이 실제값보다 덜 가변적, 미래의 방향성은 올바르게 예측하나 한기간에서 다른 기간으로의 변화 규모를 올바르게 예측하는 것은 아님 

여러 시간 단계를 앞서 예측하기

•

두 단계 이상의 먼 미래 예측

◦

yt+3y_{t+3}yt+3​ 예측 예

▪

yt+1,yty_{t+1},y_tyt+1​,yt​ 에 대한 계수를 가진 모델 필요함 

▪

yt+1,yty_{t+1}, y_tyt+1​,yt​ 값 모두 예측해서 yt+3y_{t+3}yt+3​ 예측에 이 추정값을 사용

▪

foreast 패키지의 fitted()함수 사용, 추가 파라미터 h 사용함 

◦

먼 미래의 예측을 한 결과의 분산

▪

예측 기간의 증가에 따라 예측 분산 감소

⇒유한한 이전 시점만 입력 데이터에 대한 계수에 영향 미치므로 예측 기간 떨어질수록 데이터의 중요도 떨어짐

▪

예측 기간 늘어날수록 예측은 실제 데이터의 평균에 가까워져 예측 값 및 오차항 모두에 대한 분산은 0으로 줄어듬 

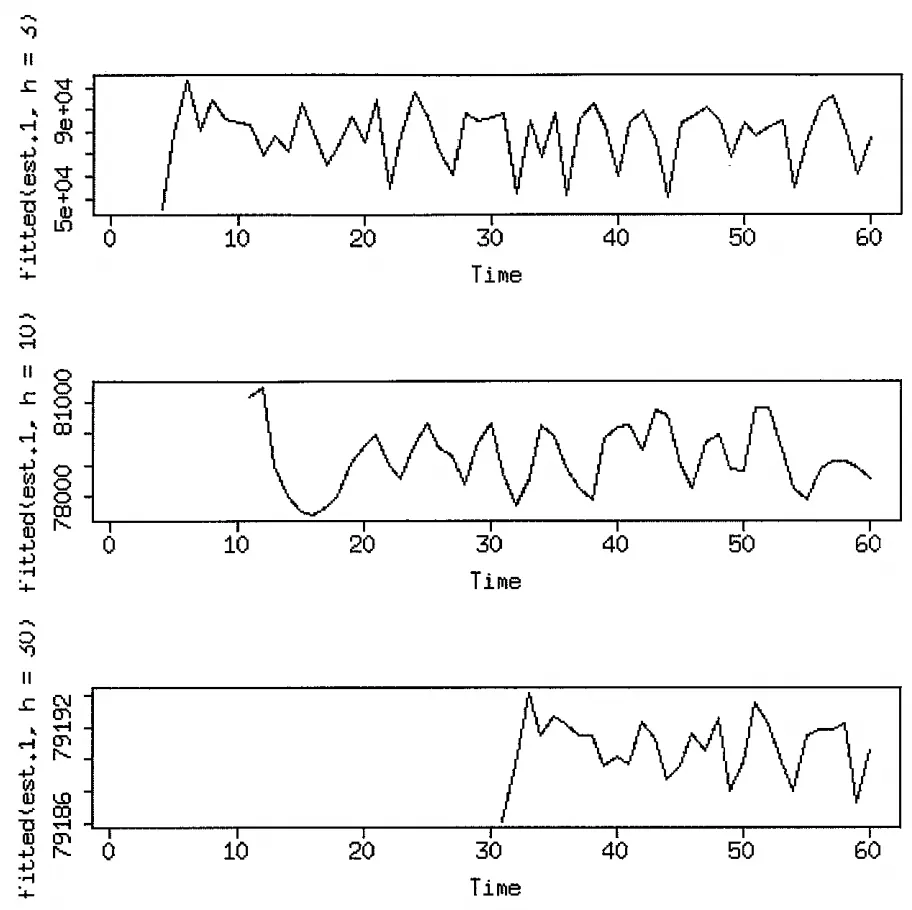
그림6-6 미래 예측 그래프 예측기간은 상단부터 3, 10 30씩 증가하도록 구성

•

AR (MA, ARMA, ARIMA)모델은 단기 예측에 가장 적합 

◦

먼 미래의 예측기간이 주어지면 그 예측 능력 상실함 

6.2.2 이동평균모델

•

이동평균 모델

◦

이동 평균 모델(MA, Moving Average Model)의 기본 개념
이동 평균 모델은 시계열 데이터 분석에서 중요한 역할을 하는 통계적 방법이다.

◦

이동 평균 모델(MA, Moving Average Model)은 시계열 데이터의 과거 ‘오차 항(error terms)‘을 사용하여 미래 값을 예측한다.

•

수학적 표현

•

이동 평균 모델의 특징

◦

과거 오차의 영향: MA 모델은 과거의 오차 항들의 영향을 받아 현재 값을 예측
이는 시계열 데이터에서 무작위 변동성을 설명하는 데 유용(Random Fluctuations)

◦

차수의 결정: MA 모델에서는 ‘q’라는 차수를 결정해야 하며, 이 차수는 과거의 몇 개의 오차 항을 현재 값의 예측에 사용할지 결정

◦

단기 예측에 유용: MA 모델은 단기 예측에 주로 사용. 이는 과거의 오차 항이 미래 값을 예측하는 데 큰 영향을 미치기 때문

•

 이동 평균 모델의 활용

◦

금융 시장 분석: 주식 시장이나 환율 같은 금융 데이터의 단기적인 변동성을 분석하는 데 자주 사용

◦

기상 데이터 예측: 단기 기상 조건의 변동을 예측하는 데 효과적

◦

수요 예측: 소매업에서 상품의 단기 수요 변동을 예측하는 데 활용될 수 있음

•

이동 평균 모델의 한계

◦

장기 예측의 한계: 오차 항의 영향이 시간이 지남에 따라 감소하기 때문에 MA 모델은 장기 예측에는 적합하지 않음

◦

비정상 시계열 데이터에의 적용성: 비정상 시계열 데이터에는 추가적인 처리가 필요할 수 있음

•

Python 구현 예제

import pandas as pd import numpy as np import matplotlib.pyplot as plt from statsmodels.tsa.arima.model import ARIMA from sklearn.metrics import mean_squared_error

예제 데이터 생성

data = np.random.randn(100).cumsum() + 100

데이터를 pandas Series로 변환

ts = pd.Series(data)

학습 데이터와 테스트 데이터로 분리

train, test = ts[:80], ts[80:]

이동 평균 모델 피팅

model = ARIMA(train, order=(0, 0, 60)) model_fitted = model.fit()

예측

predictions = model_fitted.predict(start=len(train), end=len(train) + len(test)-1)

테스트 데이터와 예측 결과를 시각화

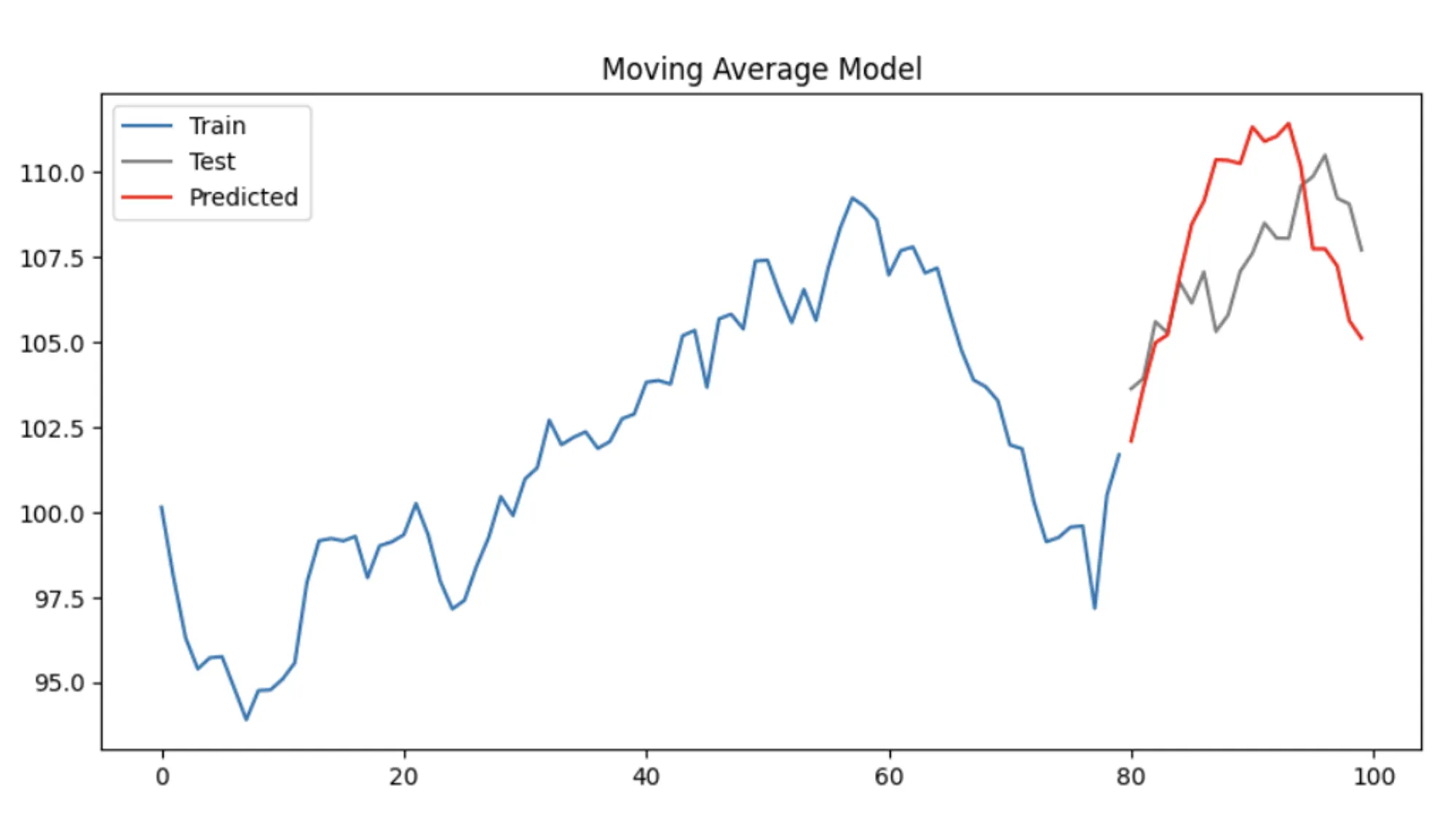
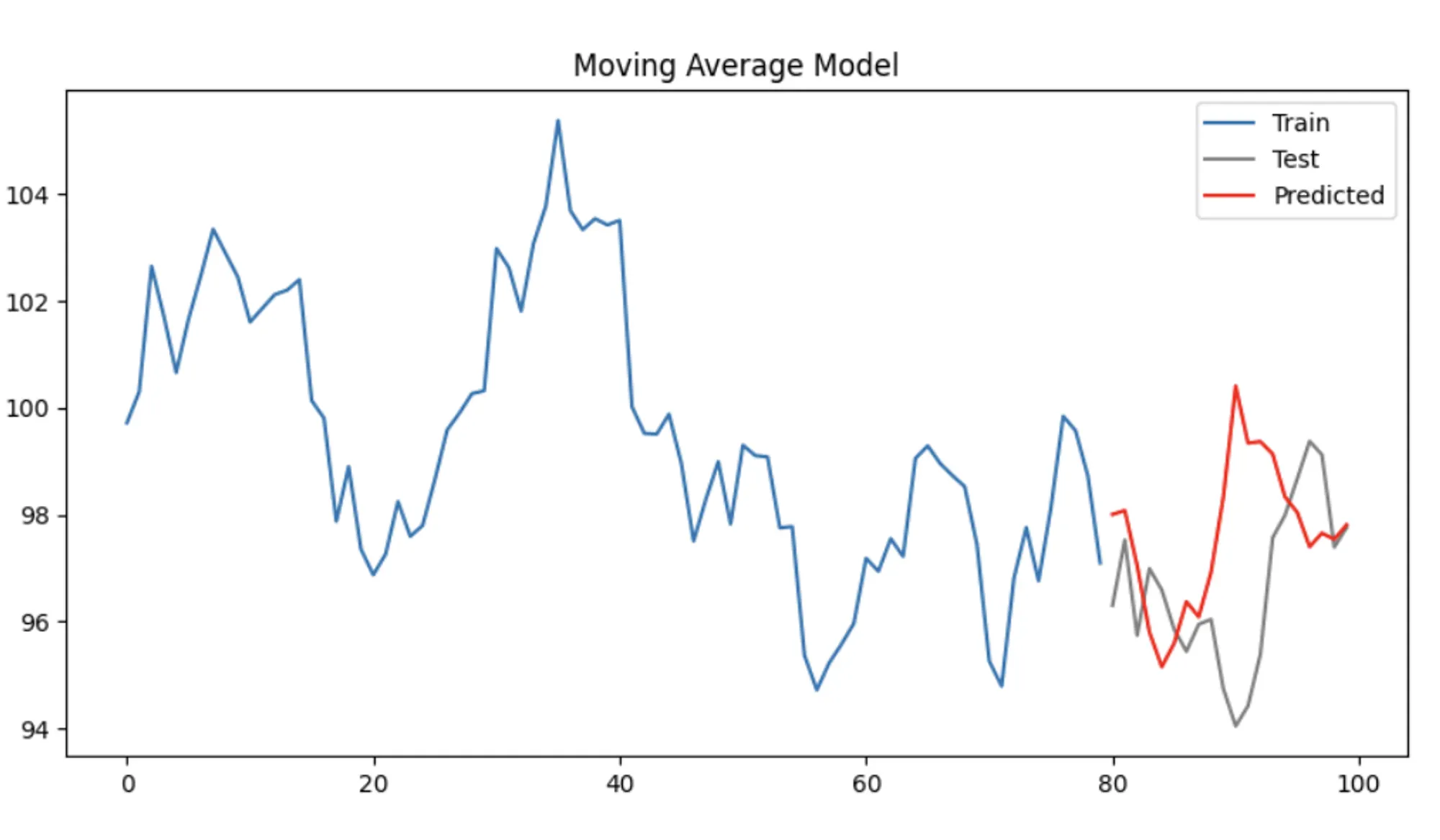
plt.figure(figsize=(10, 5)) plt.plot(train, label='Train') plt.plot(test.index, test, label='Test', color='gray') plt.plot(test.index, predictions, label='Predicted', color='red') plt.title('Moving Average Model') plt.legend() plt.show()

모델의 성능 평가

mse = mean_squared_err

이 예제는 이동 평균 모델의 기본적인 구현과 활용 방법을 보여줌

•

이동 평균 모델(Moving Average, MA)에서 order 매개변수 설정은 모델이 고려할 이전 시점(error terms)의 수를 결정하는 중요한 요소
 order 매개변수는 (p, d, q) 형식으로 설정되며, 여기서 p는 자기회귀 부분의 차수, d는 차분(differencing) 횟수, q는 이동 평균 부분의 차수를 나타냄

•

이동 평균 모델에서는 p와 d는 0으로 설정하고, q값을 조정하게 됨 
여기서 q값은 이동 평균 모델에서 고려하는 이전 시점의 오차 항의 개수를 의미하며, 예제와 같이 order=(0, 0, 60)으로 설정한다면, 모델은 현재 값이 과거 60개의 오차 항에 의존한다고 가정

•

q값 설정에 있어서 고려해야 할 사항은 다음과 같다

◦

데이터의 패턴: 데이터 내에서 관찰되는 패턴과 변동성에 따라 적절한 q값을 결정해야 함. 일반적으로, 데이터에 단기적 변동성이 높으면 q값을 크게 설정할 필요가 있음

◦

계산 복잡성: q값이 클수록 모델의 계산 복잡성이 증가. 너무 높은 q값은 모델을 과도하게 복잡하게 만들고, 과적합의 위험을 증가시킬 수 있음 (overfitting)

◦

모델의 성능: 다양한 q값을 실험하여 모델의 성능을 비교하고 최적의 값을 찾아야 함. 
이를 위해 교차 검증이나 성능 지표를 사용할 수 있음(예: MSE)

•

결론

•

◦

이동 평균 모델에서 q값 설정은 데이터의 특성과 분석 목표에 따라 달라지며, 다양한 값에 대한 실험을 통해 최적의 설정을 찾는 것이 중요

◦

이동 평균 모델은 시계열 데이터 분석에서 기본적이면서도 강력한 도구

◦

단기 예측 및 무작위 변동성의 이해에 효과적이지만, 그 적용에는 데이터의 특성과 분석 목적을 고려해야 함

6.2.3 자기회귀누적이동평균 모델

•

자기회귀누적이동평균(AutoRegressive Integrated Moving Average, ARIMA)

◦

시계열 분석에 활용되는 전통적인 대표 알고리즘임.

AR(AutoRegressive) + MA(MovingAverage) + Difference(차분) : ARIMA

ARMA모델은 AR과 MA를 합친 모델로, ARIMA와는 다르다. ARMA 모델은 평균과 분산이 일정하지 않은 비정상시계열 상태에 대응하지 못하는 반면, ARIMA는 차분을 통해 Stationary한 그래프로 변환한다. 따라서 차분이 존재하지 않는 d가 0인 ARMA 모형은 정상성을 만족한다.

•

ARMA 모델 예시 : ARMA(p,q)ARMA(p,q) ARMA(p,q)

◦

ppp : order of the AR part of the model

◦

qqq : order of the MA part of the model

◦

자기회귀 모형 AR (AutoRegressive Model) : ppp

Y_t = \phi_0 + \sum(\phi_i \times Y_{t-i}) + e_t

◦

이동평균 모형 MA (Moving Average Model) : qqq

Y_t = \phi_0 + \sum(\phi_ix;r_{t-i}) + e_t - \sum(\theta_i \times e_{t-i})

symbol

◦

ARMA - example

y_t = 0.5 \times y_{t-1} + 0.24 \times y_{t-2} + e_t + 0.6 \times e_{t-1} + 0.09 \times e_{t-2}

▪

AR 항 좌변으로 이동

y_t - 0.5\times y_{t-1} - 0.24 \times y_{t-2} = e_t + 0.6 \times e_{t-1} + 0.09 \times e_{t-2}

▪

지연 연산자(L)(L)(L)로 치환

y_t - 0.5 \times L\times y_t - 0.24 \times L^2\times y_t = e_t + 0.6 \times L \times e_t + 0.09 \times L^2 \times e_t

▪

공통 인수 인수분해

(1+0.3L) \times (1-0.8L)\times y_t = (1+0.3L) \times (1+0.3L) \times e_t

◦

정리

▪

최종 값은 각 시계열의 예측 결과를 재구성하여 추출한다.

▪

AR 및 MA 모델은 시계열 데이터를 설명하기 위해 많은 파라미터를 사용하지만, ARMA를 활용하면 모수 절약 효과를 얻을 수 있음.

•

ARIMA (p,d,q)(p,d,q)(p,d,q)

◦

ARMA에 integrated(누적)을 추가한 것

y'_t = c + \phi_1y'_{t-1} + \cdot\cdot\cdot + \phi_py'_{t-p} + \theta_1\epsilon_{t-1} + \cdot\cdot\cdot ~+\theta_q\epsilon_{t-q} + \epsilon_t

Symbol

◦

ARIMA가 활용된 예시

▪

대만으로 귀항하는 항공기 여행 승객

▪

터키의 연료 유형별 에너지 수요

▪

인도의 야채 도매 시장에서의 일일 판매

▪

미국 서부의 응급실 수요

•

ARIMA 일부 예시

◦

(p,d,q):(0,0,0)(p,d,q) : (0,0,0)(p,d,q):(0,0,0) → White noise model

◦

(p,d,q):(0,1,0)(p,d,q) : (0,1,0) (p,d,q):(0,1,0) → 확률보행(random walk with drift)

◦

(p,d,q):(0,1,1)(p,d,q) : (0,1,1)(p,d,q):(0,1,1) → 지수평활(exponential smoothing)

◦

(p,d,q):(0,2,2)(p,d,q) : (0,2,2) (p,d,q):(0,2,2) → 추세를 지닌 데이터 지수평활 / 홀트의 선형 방법(Holt’s linear method)

•

수동적으로 모델을 적합시키는 방법

◦

단순성이 가장 중요한 ARIMA 모델의 파라미터 선택을 위한 발견적 방법 - (Box-Jenkins)

데이터, 시각화, 기반 지식을 사용하여 데이터에 적합한 모델의 종류를 고름.

주어진 학습용 데이터로 파라미터를 추정함.

학습용 데이터를 기반으로 모델 성능을 평가하고, 모델의 파라미터를 조정하여 성능 진단상 나타나는 약점을 해결함.

데이터 생성하기 및 Arima(1,0,1) 적용

Arima(1,0,1)은 d가 0이므로 ARMA를 의미.

#install.packages("forecast") library(forecast) set.seed(1017)

ARIMA 모델의 차수를 의도적으로 숨깁니다.

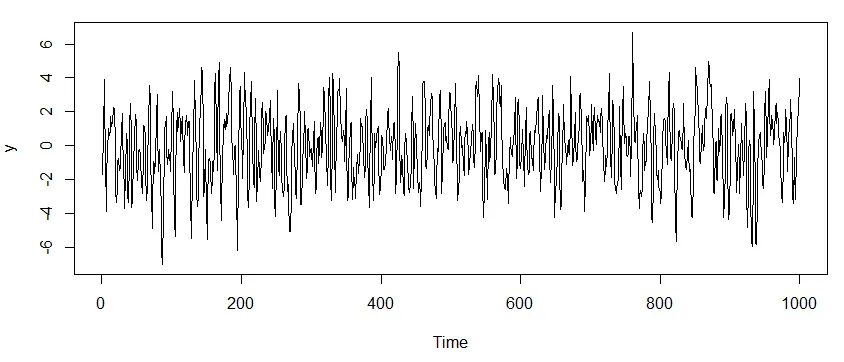
y = arima.sim(n = 1000, list(ar = ###, ma = ###)) plot(y, type = 'l')

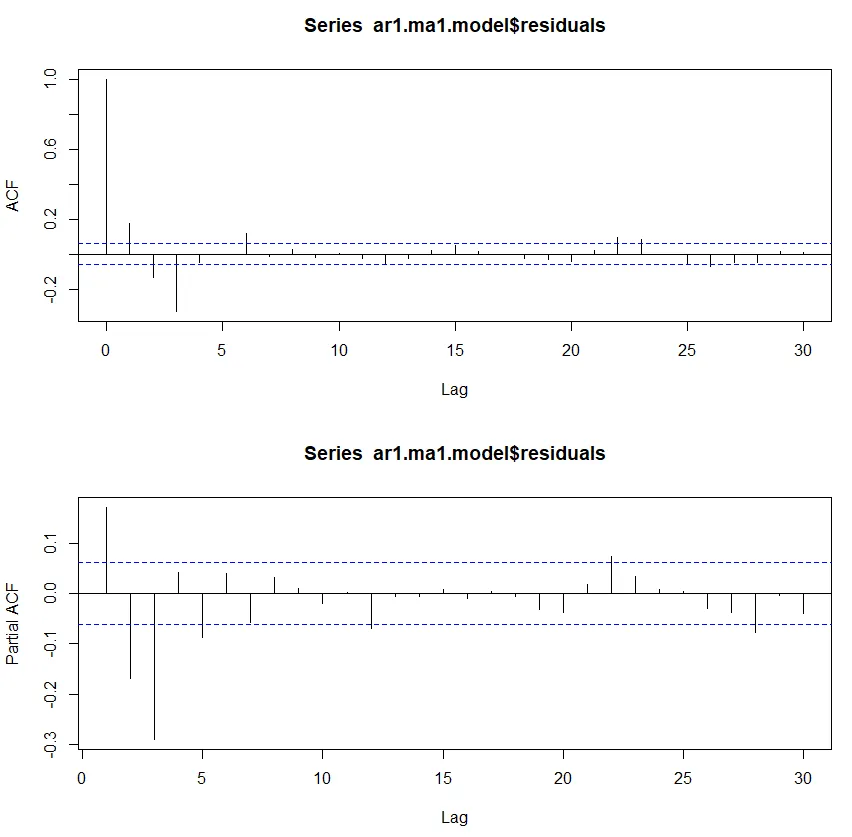
ar1.ma1.model = Arima(y, order = c(1,0,1)) par(mfrow = c(2,1)) acf(ar1.ma1.model$residuals) pacf(ar1.ma1.model$residuals)

◦

잔차가 PACF에서 큰 값을 보여주고 있어 자기회귀 동작을 완전히 설명하지 못함. 

◦

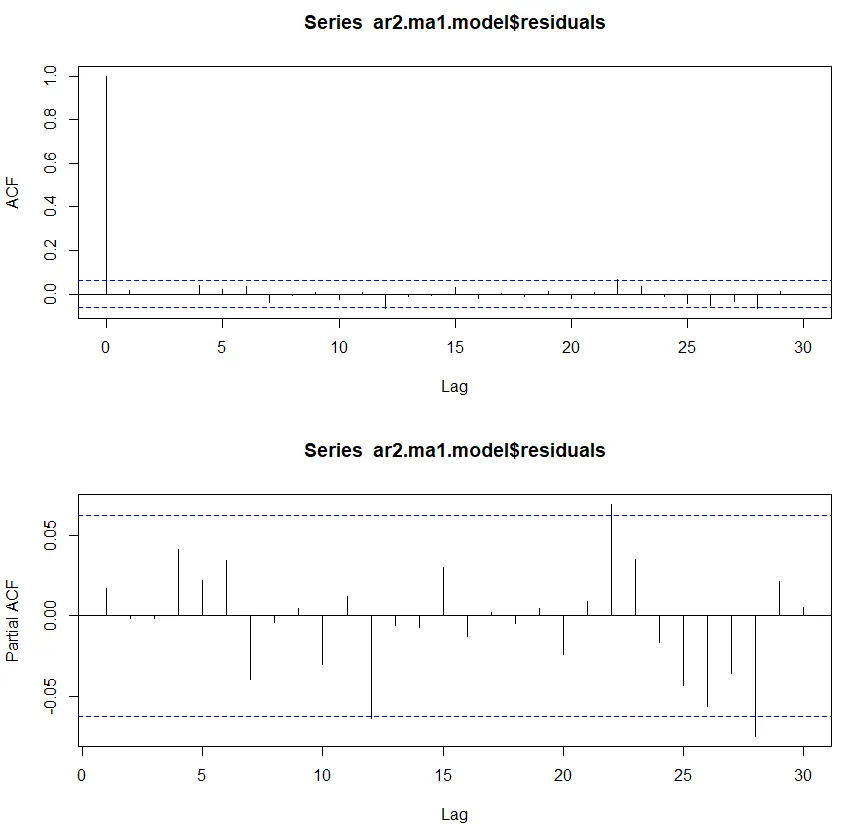
따라서, AR 요소에 대해 높은 차수를 가진 ARIMA(2,0,1) 모델을 테스트 함.

◦

결과적으로 ACF와 PACF에서 더 좋은 결과가 나오지 않음.

◦

모델의 단순성과 ARIMA 모델의 과적합에 대한 위험성을 고려하여 이 이상의 튜닝은 하지 않음.

◦

나머지도 수행해보기 → ARIMA(2,0,2)

◦

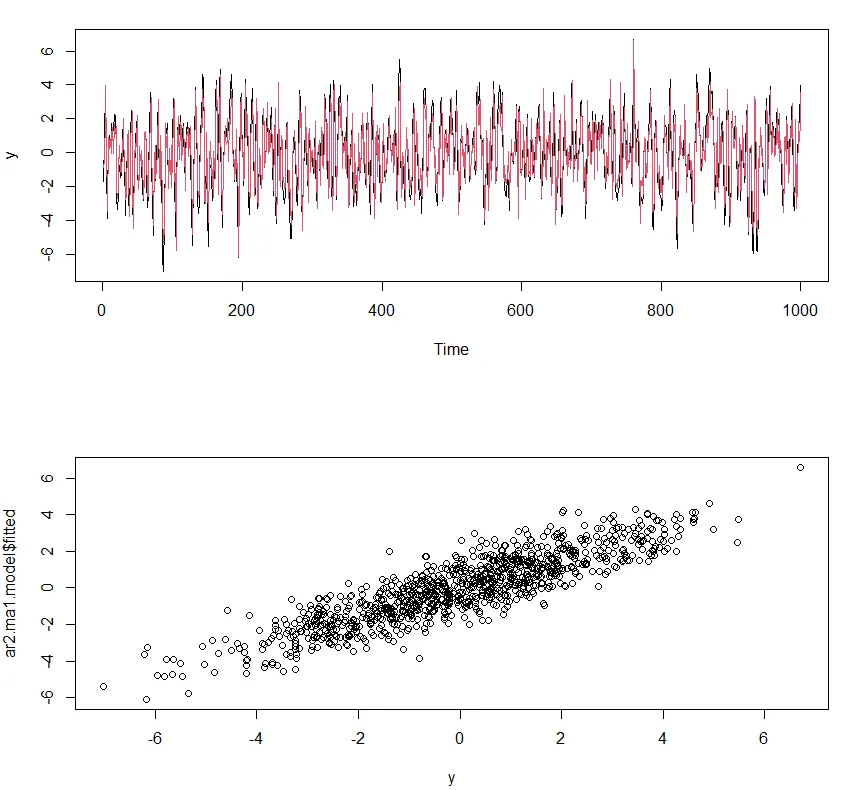
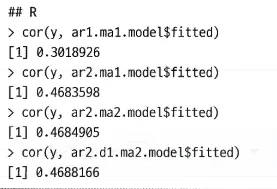
적합된 모델의 예측과 실젯값 사이의 상관관계를 분석하여 모델을 빠르게 비교하는 방법.

ARIMA(1,0,1) 모델에서 ARIMA(2,0,1) 모델로 전환하면서 상관계수가 0.3에서 0.47로 바뀌는 것을 통해 개선이 이루어진 것을 확인할 수 있음.

그 외에 복잡성을 더 추가한 세 번째와 네 번째에서는 크게 개선되지 않음.

따라서, ARIMA(2,0,1) 모델로 충분히 개선되었으며 AR 또는 MA 구성요소를 그 이상 향상하여 적합시킬 필요가 없다는 결론에 수렴함.

•

자동으로 모델을 적합시키는 방법

◦

AIC와 같은 다양한 정보손실 기준을 토대로 이루어짐.

est = auto.arima(demand[["Banking orders (2)"]],
                 stepwise = FALSE, ## 느리지만 좀 더 완전한 검색 수행
                 max.p = 3, max.q = 9)
R
복사

Stepwise

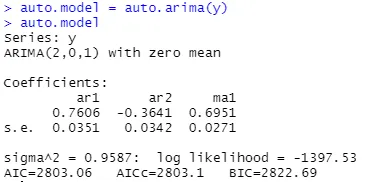
atuo.model = auto.arima(y)
auto.model
R
복사

6.2.4 벡터자기회귀

•

VAR(Vector Autoregression Model)

◦

‘Vector’는 여러 개의 값을 포함하는 데이터를 나타내는 수학적 용어

◦

각 변수들을 하나의 벡터로 표현하여 변수들 간의 상호작용을 묘사해 변수들 간의 관계를 더 명확하게 표현

•

여러 변수에 대한 AR(p)\mathrm {AR(\mathit {p})}AR(p) 모델 생성

◦

다변량 데이터 적용 가능

◦

적합은 모든 변수에 대해 균등하게 이루어짐

◦

시계열이 정상이 아닐 때 차분이 적용될 수 있음

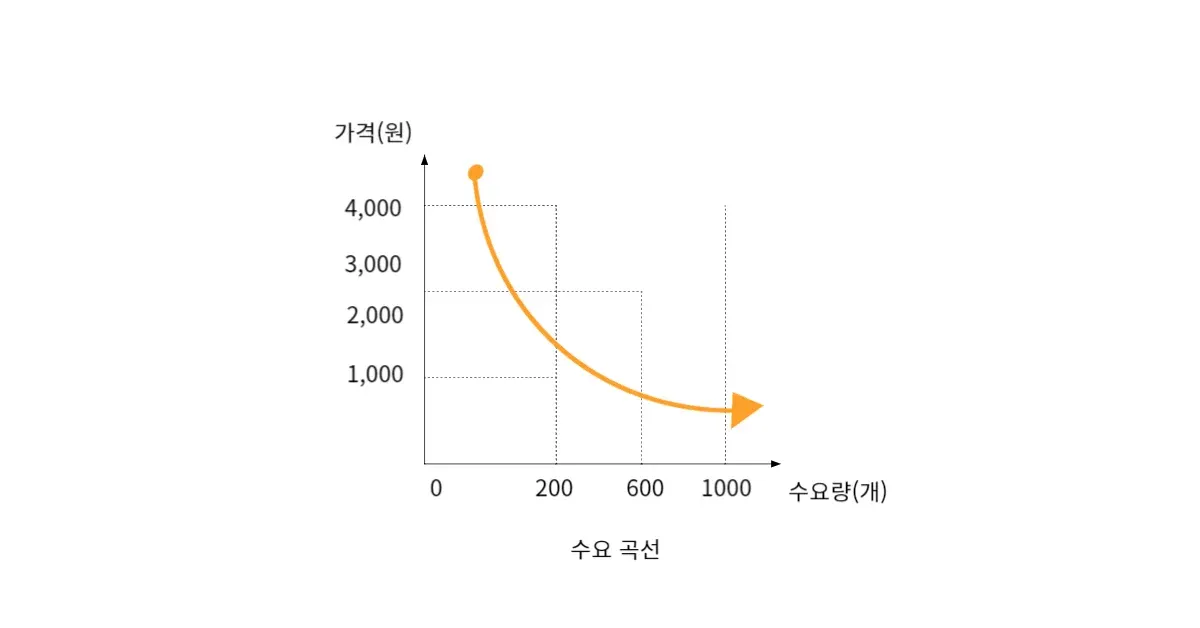
내생변수와 외생변수 내생변수는 모형 안에서 그 값이 결정되는 변수로, 모형 내에서 결과에 직접적인 영향을 주는 변수를 말함 외생변수는 모형 밖(외부)에서 사전적으로 주어지는 변수로, 모형 안의 결과에 영향을 주는 변수를 말함 [예시] 수요 곡선(가격이 오르면 수요량이 감소하는 모형) 예시 가격은 모형 내에 있는 내생변수로서, 모형 내에서 결과(수요량)에 직접적인 영향을 줌. 하지만 가격이 변하지 않았는데도 소득 증가, 관광객 증가, 선호도 변화 등으로 인해 수요가 증가할 수 있음(수요 곡선 모형에 없는 변수들임에도 불구하고) ⇒ 이렇게 모형 밖(외부)에서 결정되는 변수이지만 모형 안의 결과에 영향을 주는 변수를 외생변수라고 함

수요 곡선

•

시간 ttt에서, 차수가 2인 벡터 자기회귀(VAR) 방정식

◦

각 변수를 y1,t,y2,t,y3,t\mathrm y_{1, t}, \mathrm y_{2, t}, \mathrm y_{3, t}y1,t​,y2,t​,y3,t​라고 표기 (변수 3개)

◦

차수가 2인 경우 (과거 데이터를 2단계까지 고려하여 현재 값 예측)

\mathrm y_{1,t} = \phi_{01} + \phi_{11,1} \times \mathrm y_{1,t-1} + \phi_{12,1} \times \mathrm y_{2,t-1} + \phi_{13,1} \times \mathrm y_{3,t-1} + \phi_{11,2} \times \mathrm y_{1,t-2} + \phi_{12,2} \times \mathrm y_{2,t-2} + \phi_{13,2} \times \mathrm y_{3,t-2} \\ \mathrm y_{2,t} = \phi_{02} + \phi_{21,1} \times \mathrm y_{1,t-1} + \phi_{22,1} \times \mathrm y_{2,t-1} + \phi_{23,1} \times \mathrm y_{3,t-1} + \phi_{21,2} \times \mathrm y_{1,t-2} + \phi_{22,2} \times \mathrm y_{2,t-2} + \phi_{23,2} \times \mathrm y_{3,t-2}\\ \mathrm y_{3,t} = \phi_{03} + \phi_{31,1} \times \mathrm y_{1,t-1} + \phi_{32,1} \times \mathrm y_{2,t-1} + \phi_{33,1} \times \mathrm y_{3,t-1} + \phi_{31,2} \times \mathrm y_{1,t-2} + \phi_{32,2} \times \mathrm y_{2,t-2} + \phi_{33,2} \times \mathrm y_{3,t-2}

행렬 곱셈 행렬을 사용하면 더욱 간편하게 작성 가능

\mathrm y = \phi_0 \ + \phi_1 \times \mathrm {y_{t-1}} + \phi_2 \times \mathrm {y_{t-2}}

y와

\phi_{0}

는 3

\times

1 행렬이며, 다른

\phi

행렬의 모양은 3

\times

3임

•

간단한 경우에도 모델의 파라미터 개수가 빠르게 증가하는 것을 확인 가능

•

예를 들어 lag이 ppp개, 변수가 NNN개 있을 때 각 변수에 대한 예측 방정식은 1+p×N21+p \times N^21+p×N2 의 총 변수로 변환됨

◦

변수의 개수가 시계열의 개수에 비례하여 O(N2)O(N^2)O(N2)로 증가

⇒ 데이터에 새로운 변수를 추가할 때 실제로 모델에 유의미한지 신중하게 고려해야 함 (모델의 복잡성, 과적합 등의 문제)

VAR의 활용성

•

VAR은 다변량 자기회귀 모델로, 모든 변수가 서로 영향을 미치는 것을 가정하기 때문에 모델링 및 적합도 판단에 어려움이 있음

•

변수 간의 종속 관계 여부 검정, 변수들의 특정 관계를 정의하지 않고 여러 변수를 예측하는 경우, 특정 변수 값의 예측 변동을 초래하는 지를 결정할 때 활용 가능

[예시]

은행 주문(banking order) 예측

•

변수를 균등하게 다루는 방식 

•

교통 관제 부문 주문(order from the traffic control sector) 변수의 사용 고려 
→ 재정 주문(fiscal sector)의 과거 주문에 관련해 독립적 정보를 제공할 가능성 있음

•

vars 패키지의  VARselect() 메서드 → 사용할 파라미터 결정

•

평균을 포착하기 위해 const항을 사용해 모델의 방정식에 절편을 포함

◦

모델링 할 데이터가 평균을 중심으로 일정한 범위 내에서 변동하는 경우, 모델은 데이터의 중심에 대한 정보를 포착하기 위해 상수항을 포함

•

drift(추세항)와 const(상수항)를 모두 사용하거나 두 개 모두 사용하지 않을 수 있음

◦

위 예제에서는 데이터에 가장 적합한 ‘const’ 선택

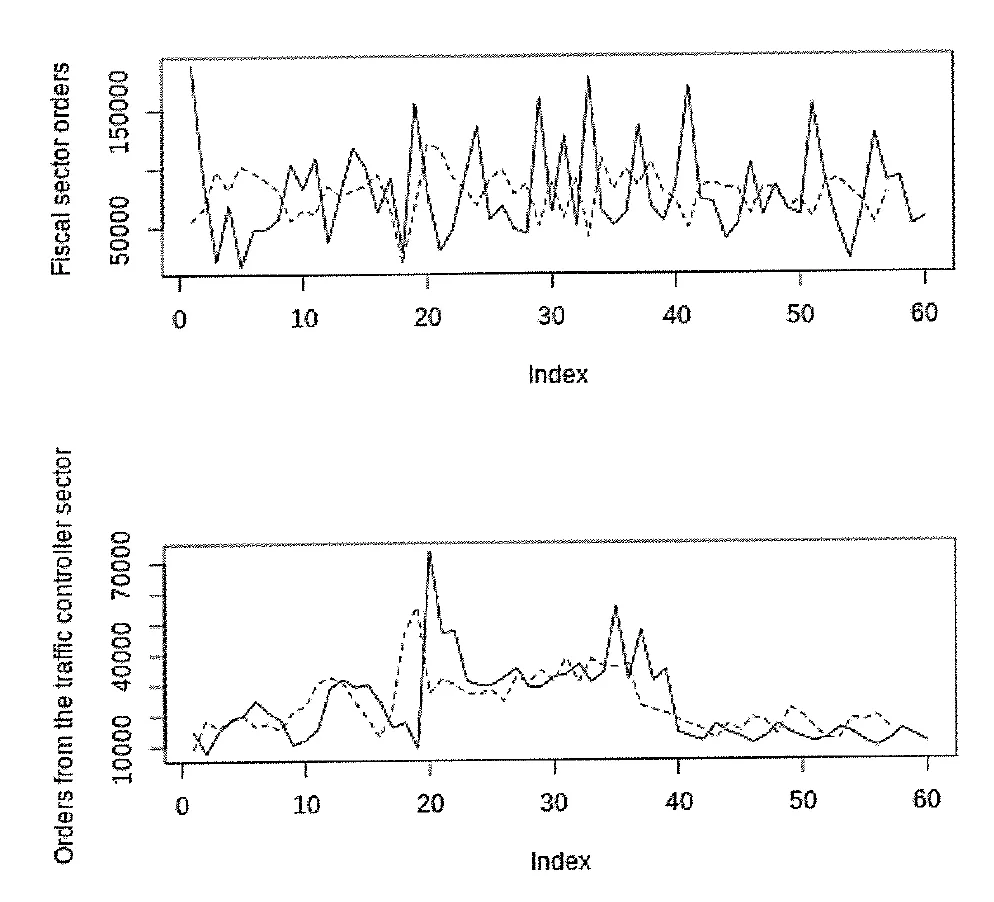
실선 : 실제값 / 파선 : 예측값

•

상단 그래프 : 재정 부문의 주문

•

하단 그래프 : 교통 관제 부문의 주문

⇒ 상단 그래프는 전형적인 예측과 같이 느리게 변환하지만 하단 그래프는 실제 변화가 발생하기 전에 미리 예측이 이루어진 것으로 보임

•

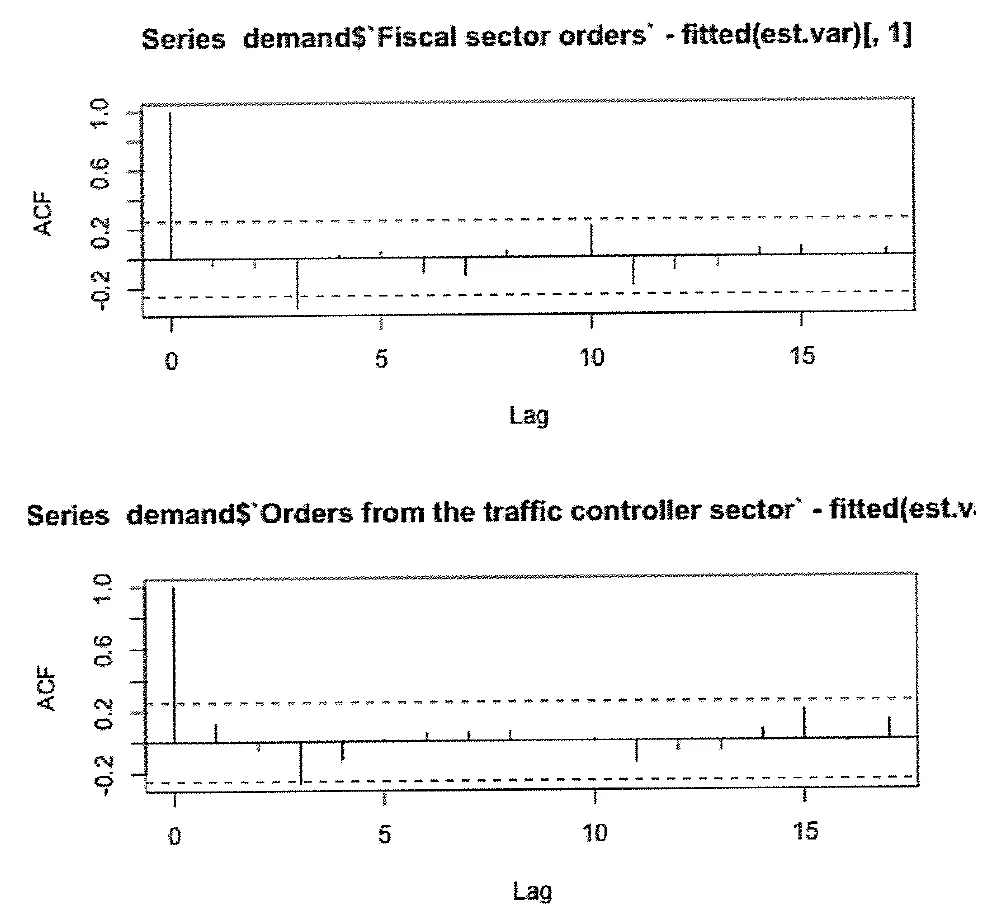
각 시계열의 잔차에 대한 자기상관함수 그래프

•

모델로 설명하기 어려운 오차에 대한 임계치를 넘는 자기 상관이 있음(Lag 3)

•

ACF (Autocorrelation Function)는 잔차에 자기상관이 없음을 명확히 보여주지 않음

•

순차적 상관관계를 위해 포트맨토 검정(portmanteau test)을 적용.

◦

주어진 잔차 시계열의 자기상관계수가 0이라는 귀무가설

◦

vars 패키지의 serial.test() 메서드로 접근할 수 있음.

•

p−{p-}p−값이 매우 크면 잔차에 연속적인 상관관계가 없다는 귀무가설을 기각할 수 없음

◦

p−p-p−값이 작을수록(예: 0.05보다 작을 때) 귀무가설을 기각 → 모델 비적합

◦

p−p-p−값이 크면(예: 0.05보다 크거나 같을 때) 귀무가설을 기각하지 않음 → 모델 적합

•

모델은 허용 가능한 작업을 수행한다는 추가 증거를 제시할 수 있음

•

VARIMA

◦

VAR 모델에 ARIMA 모델의 차분(Differencing) 과정을 추가하여 정상성을 확보한 모델 (VAR + ARIMA)

◦

VAR의 성능이 상대적으로 괜찮기 때문에 VARIMA 모델을 많이 사용하지는 않음

•

CVAR

◦

공적분된 벡터 자기회귀(Cointegrated Vector AutoRegression)

◦

시계열 변수들이 공적분 관계(cointegration)를 가질 때 사용하는 방법

▪

각 시계열 데이터가 개별적으로는 정상성을 가지지 않지만, 그들의 선형 결합이 정상성을 가지는 경우
(시계열 데이터가 장기적으로 평형을 유지하면서도 각각은 자기회귀 모형 또는 다른 비정상적인 특성을 가질 수 있음)

6.2.5 통계 모델의 변형

계절성 ARIMA

•

기존 ARIMA 모델에 계절 변동을 반영

•

SARIMA 모델은 ARIMA(p,d,q)×(P,D,Q)m(p, d, q) \times (P, D, Q)m(p,d,q)×(P,D,Q)m과 같이 표현

◦

mmm(또는 sss) : 계절성 주기 → 예) 월별 계절성을 나타낼 때 m=12m=12m=12

◦

(p,d,q)(p, d, q)(p,d,q)는 비계절 요인, (P,D,Q)(P, D, Q)(P,D,Q)는 계절 요인을 나타냄

•

계절성을 고려하여 모델을 구성하며, 시간적으로 근접한 계절 간의 영향을 인식하여 예측을 수행 
(예: 6월에 높은 매출이 발생했다면, 모델은 이를 고려하여 다음 해의 6월에도 높은 매출이 발생할 것으로 예측)

ARCH

•

자기회귀 조건부 이분산성(AutoRegressive Conditional Heteroskedasticity)

•

대부분 금융 업계에서 사용

•

과거의 변동성이 현재의 변동성에 영향을 미침

•

주가 자체보다는 과거의 변동성의 패턴을 따르는 자기회귀 과정으로 모델링

계층적 시계열 모델

계층적 시계열이 발생하는 경우

•

회사 제품의 월별 총 수요는 SKU (Stock Keeping Unit, 재고 단위 관리) 번호로 세분화됨

•

전체 유권자의 주간 정치 여론 조사를 여성/남성 또는 히스패닉/아프리카계 미국인과 같은 인구통계(demographics)로 세분화

•

EU에 방문하는 일일 총 관광객 수를 EU의 각 회원국을 방문한 관광객 수로 세분화

R의 hts패키지

•

계층적 시계열 데이터를 시각화하고 이러한 데이터에 대한 예측을 수행하는 데 사용

•

계층적으로 가장 저수준의 여러 가지 예측을 한 다음(가장 세분화된), 이를 집계하여 고수준의 예측을 수행

◦

가장 고수준의 예측을 한 다음, 기록된 집계 요소의 비율을 기반으로 저수준의 예측을 수행

◦

저수준 예측에서 정확도가 떨어지는 경향을 보이지만, 시간에 따른 집계 비율의 변화를 예측하는 다양한 기법을 함께 사용하면 정도를 완화할 수 있음

◦

고수준/저수준 예측의 장점을 취해 중간 수준의 예측을 수행하는 ‘중간적’ 접근법 선택 가능

•

일반적으로 그 지점의 위, 아래로 전파되면서 다른 수준의 예측을 이어서 수행함.

•

결론적으로 hts 패키지의 동작 방식은 모든 수준에 대한 예측이 서로 독립적으로 수행하고 하인드먼 방법과의 일관성을 보장하기 위해 각 예측들을 결합함.

⇒ 이번 장에서 논의한 여러 통계 모델은 시계열의 계층 수준에 상관없이 적용 가능. 계층적이라는 것은 핵심이 되는 모델을 감싸는 래퍼 역할을 함.

6.3 시계열 통계 모델의 장단점

장점

•

통계 모델은 간단하고 투명해서 모델의 파라미터 측면을 보면 명확하게 이해할 수 있음

•

통계 모델을 정의하는 간단한 수학적 표현을 통해 통제적으로 관심 속성 도출 가능

•

어느 정도 작은 데이터셋에 적용해도 여전히 좋은 결과를 얻을 수 있음

•

간단한 통계 모델과 이를 변형한 모델은 상당히 좋은 성능(머신러닝의 과적합 위험성 없이 좋은 성능을 얻을 수 있음)

•

모델의 차수 선택 및 파라미터 추정에 대해 잘 개발된 자동화 방법론은 예측을 간단하게 만듦

단점

•

통계 모델은 매우 간단해서 데이터셋이 커졌을 때 항상 성능 향상이 보장되지 않음. (대규모 데이터셋으로 작업한다면 머신러닝 모델 및 신경망 방법이 적합)

•

통계 모델은 분포보다는 분포의 평균값 추정에 집중함 → 표본의 분산을 도출할 수 있지만 이는 모델을 고를 때 선택한 모든 것에 대한 불확실성을 제한된 방식으로만 표현함. 기본 모델이 모델을 선택할 때 선택한 모든 선택과 관련된 불확실성을 표현하는 제한된 방법만 제공함.

•

통계 모델은 비선형적 행동을 다루기 위해 구축된 것이 아니라서 비선형 관계가 많은 데이터를 설명하는 데 적합하지 않음.

Reference

•

케인스, 독립변수, 종속변수, 내생변수, 외생변수, naver blog (link)