서론
•
6-7장(시계열 통계 및 상태공간 모델): AR, MA, ARIMA, Kalman filter, HMM, BSTS 등
→ 원본 시계열 데이터를 사용하여 모델을 적합(fitting)시키는 방법들
•
비선형 문제에는 머신러닝 기반 시계열 모델이 적합하고, 이를 위해서는 시계열 원본 데이터 뿐만 아니라 다양한 특징 추출과 선택 과정을 통해 모델에 최적화된 학습 데이터셋을 준비해야 한다.
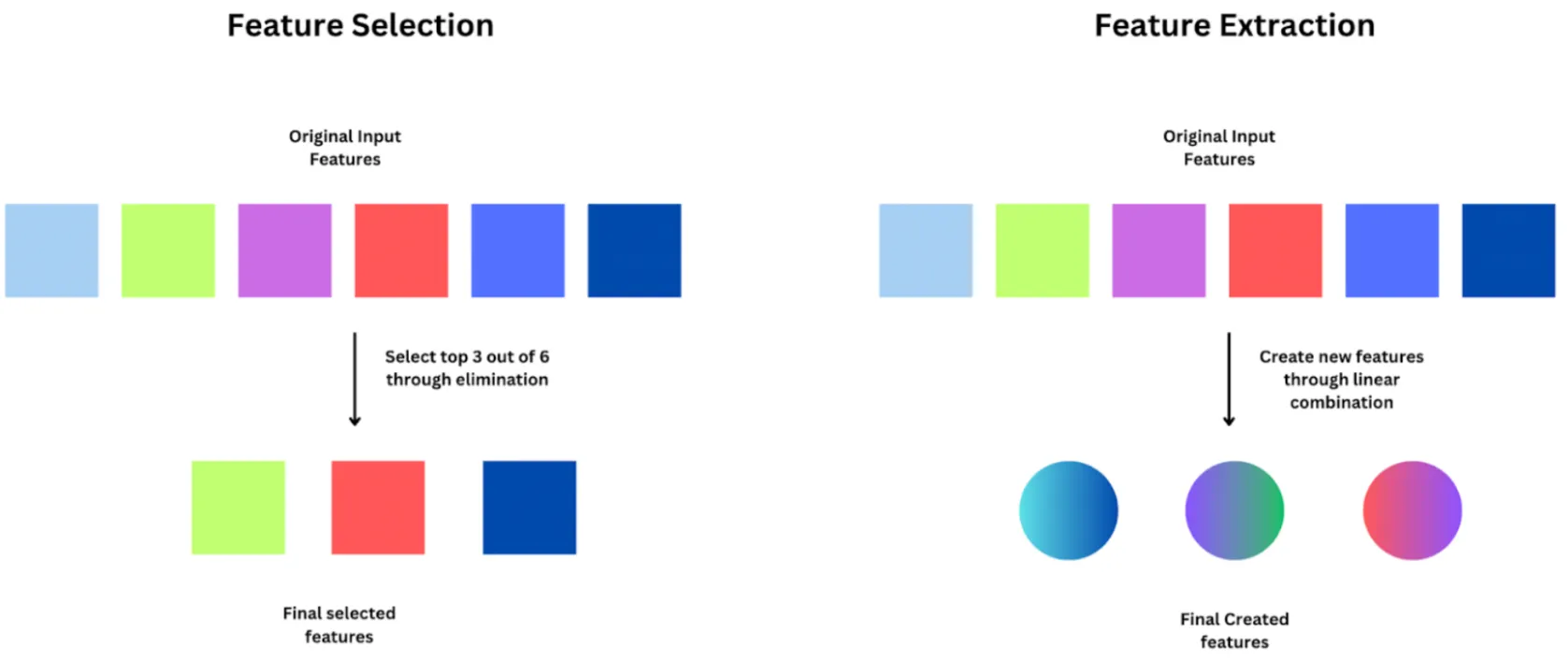
특징 추출(Feature extraction)
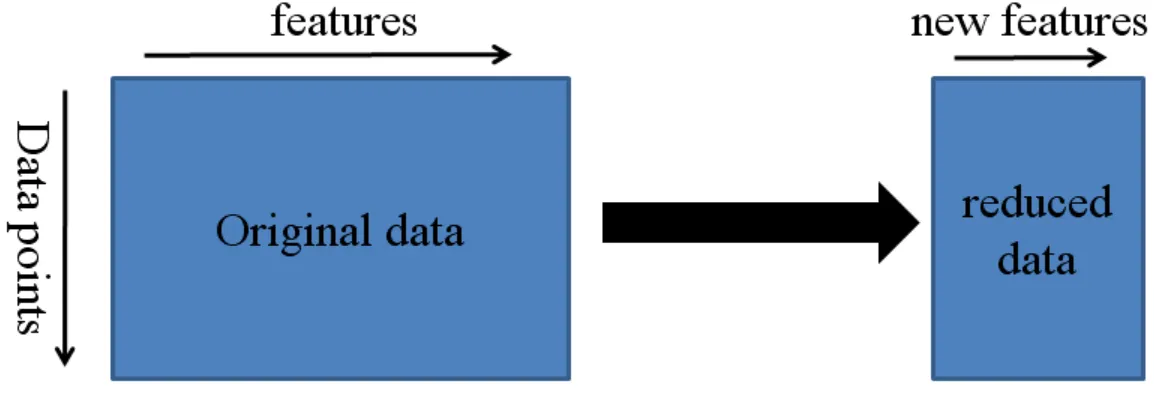
차원축소(Dimension reduction) 기법이며, 기존 특징들의 조합으로 유용한 특징들을 새롭게 생성하는 과정이며, 일반적으로 고차원의 특징 공간을 저차원의 새로운 특징 공간으로 투영함(예: 주성분 분석, 선형판별 분석)|
특징 선택(Feature selection)
문제와 관련 없거나 중복되는 특징들을 제거하여 효과적으로 데이터셋을 축소하는 과정
•
8장에서는 머신러닝 기반 시계열 모델(9장)을 만드는데 필요한 학습 데이터셋을 준비하는 과정으로 특징 추출과 선택에 대한 내용을 다룬다.
8.1 입문자를 위한 예제
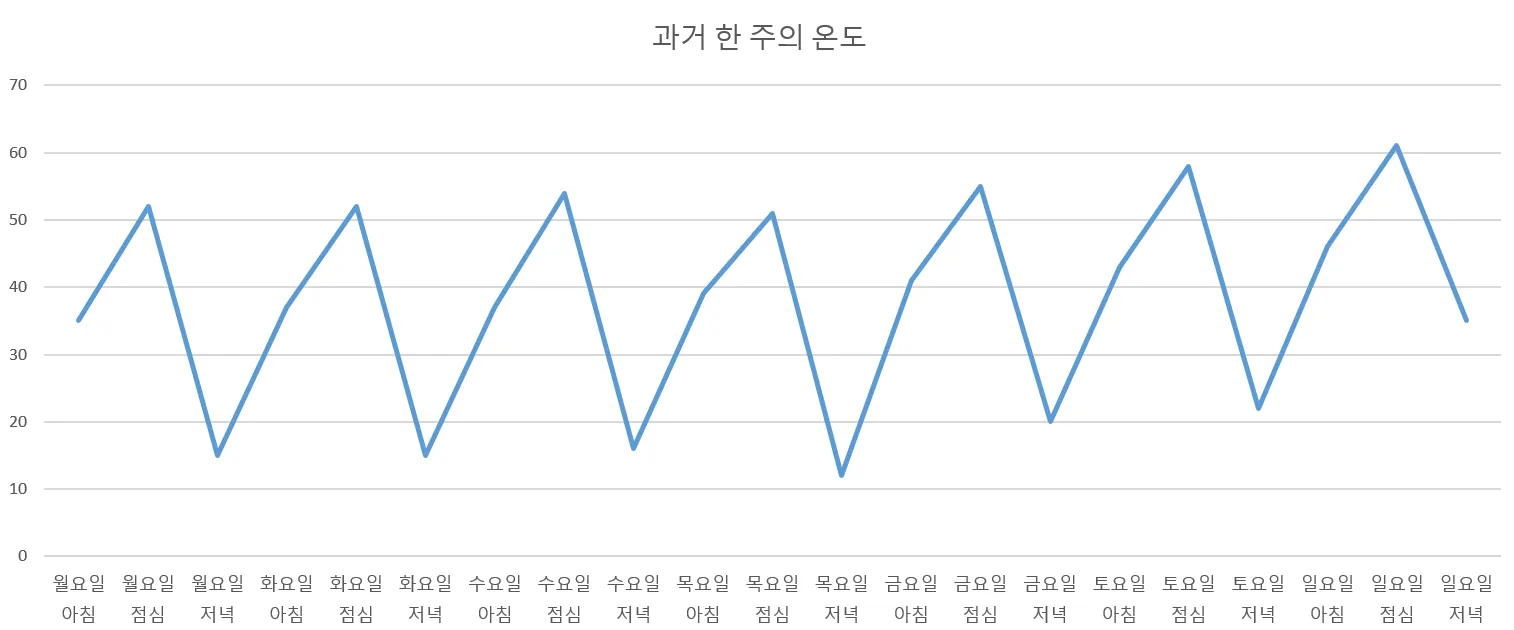
<표. 한 주 기간의 아침/점심/저녁 온도>
•
참고: 화씨 61°F 섭씨 16°C, 화씨 12°F 섭씨 -11°C
시간 | 온도(°F) |
월요일 아침 | 35 |
월요일 점심 | 52 |
월요일 저녁 | 15 |
화요일 아침 | 37 |
화요일 점심 | 52 |
화요일 저녁 | 15 |
수요일 아침 | 37 |
수요일 점심 | 54 |
수요일 저녁 | 16 |
목요일 아침 | 39 |
목요일 점심 | 51 |
목요일 저녁 | 12 |
금요일 아침 | 41 |
금요일 점심 | 55 |
금요일 저녁 | 20 |
토요일 아침 | 43 |
토요일 점심 | 58 |
토요일 저녁 | 22 |
일요일 아침 | 46 |
일요일 점심 | 61 |
일요일 저녁 | 35 |
•
온도 데이터에 대한 시각화: 온도가 주기성(일별 순환)을 가지는 동시에 전반적으로 증가하는 추세
위 시계열 데이터의 패턴을 어떻게 집약적으로 표현할 수 있을까주기성(cycle), 추세(trend), 시간대 별 평균(아침/점심/저녁) 등
특징 추출 및 선택 예1.
21개의 값으로 구성된 원본 시계열 → 원본 정보를 최대한으로 보존하는 2~5개의 값으로 요약(특징 추출)
2.
생성된 특징들을 검토하여 의미 없는 것들을 제거(특징 선택)
8.2 특징 계산 시 고려 사항
특징 추출 과정에서 고려해야 되는 사항•
추출하고자 하는 특징에 타당한 근거가 있는지?
•
추출된(생성된) 특징으로부터 유의미한 통찰을 이끌어 낼 수 있는지?
•
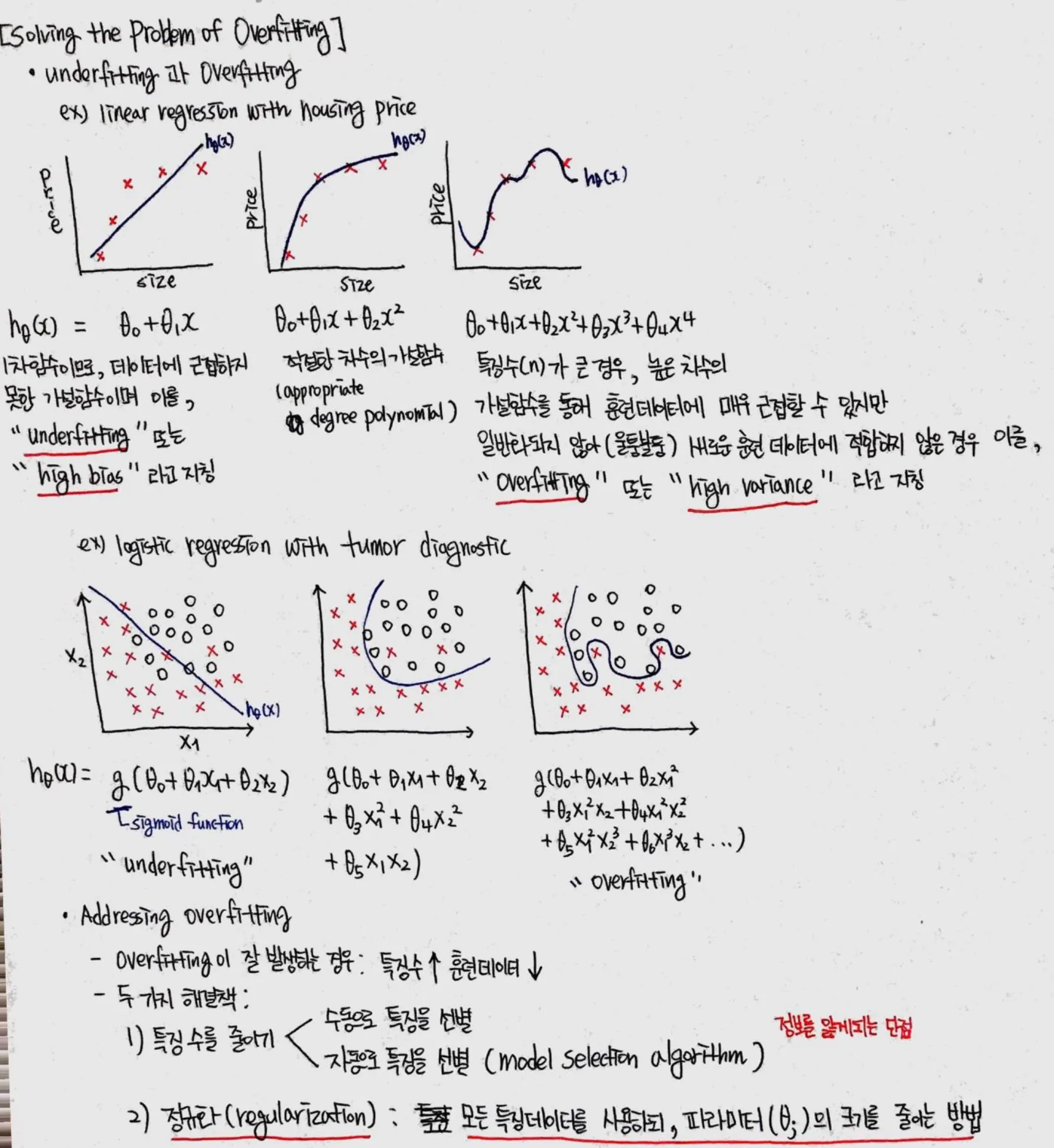
추출된 특징으로 인해 모델 학습 과정에서 과적합(overfitting)이 발생할 가능성은 없는지?
과적합 문제의 원인 및 해결 방법 (Machine Learning, Coursera, 스터디 노트)
8.2.1 시계열의 특성
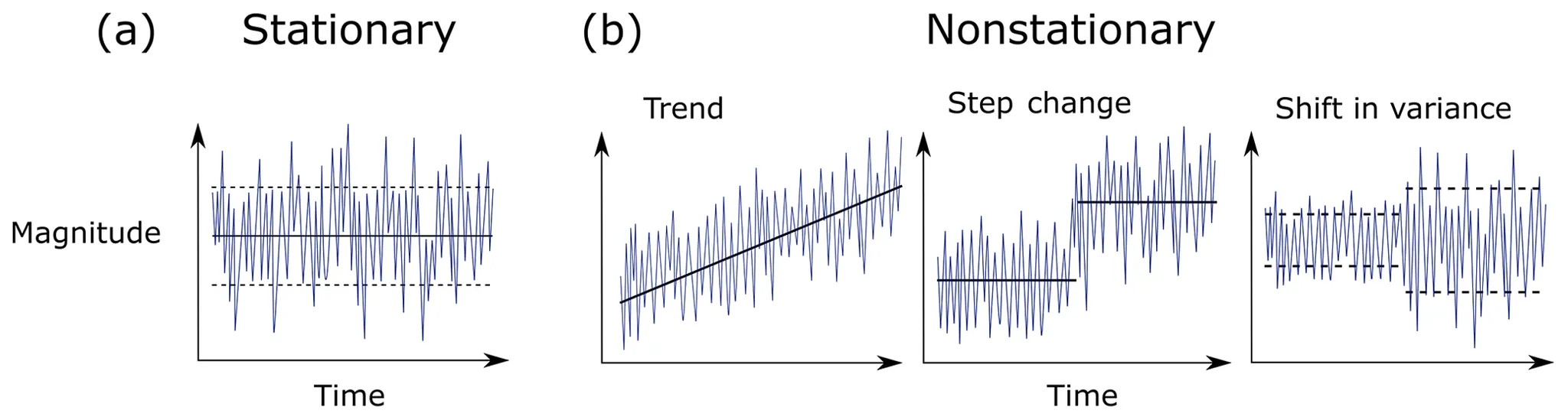
정상성시계열의 여러 특징들은 정상성(stationarity)을 가정한다(예: 평균, 분산).
시계열 데이터를 모델링할 때 일반적으로 정상 시계열이거나 아니면 적어도 어고딕(ergodic) 성질을 만족하는 것을 가정한다.
Ergodicity시계열에서 정의하는 ergodicity는 시평균과 앙상블 평균이 같은 성질로 정의된다.
•
확률 과정(stochastic process): 시간에 따라 일어나는 일들이 확률에 따라 결정되는 과정
◦
시계열: 확률과정을 통해 발생한 데이터들의 수열
•
확률 과정에 대한 표본 함수(sample function): 확률 과정으로부터 나올 수 있는 가능한 모든 시간 함수 중 하나
◦
예: 1번 국도에서 측정되는 도로 소음 신호,
•
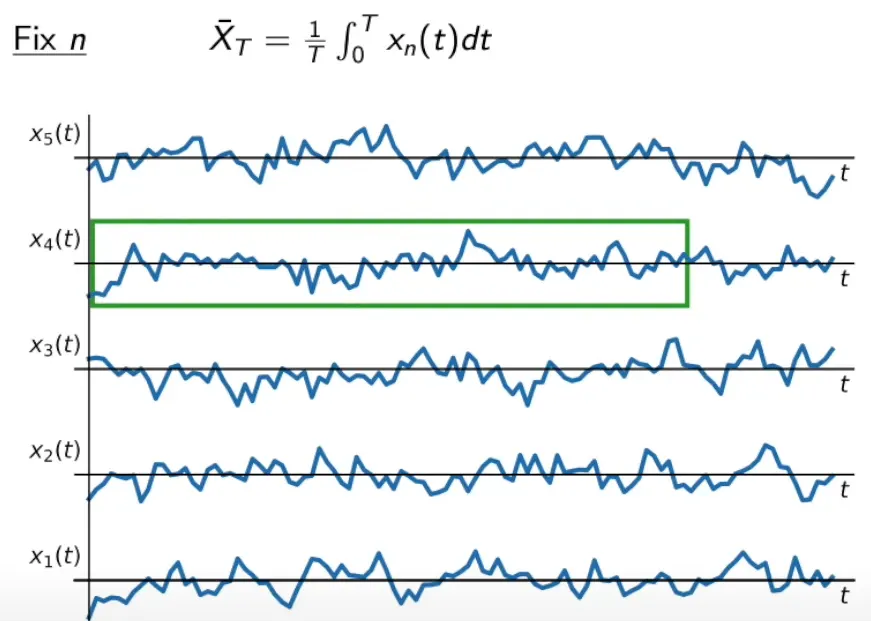
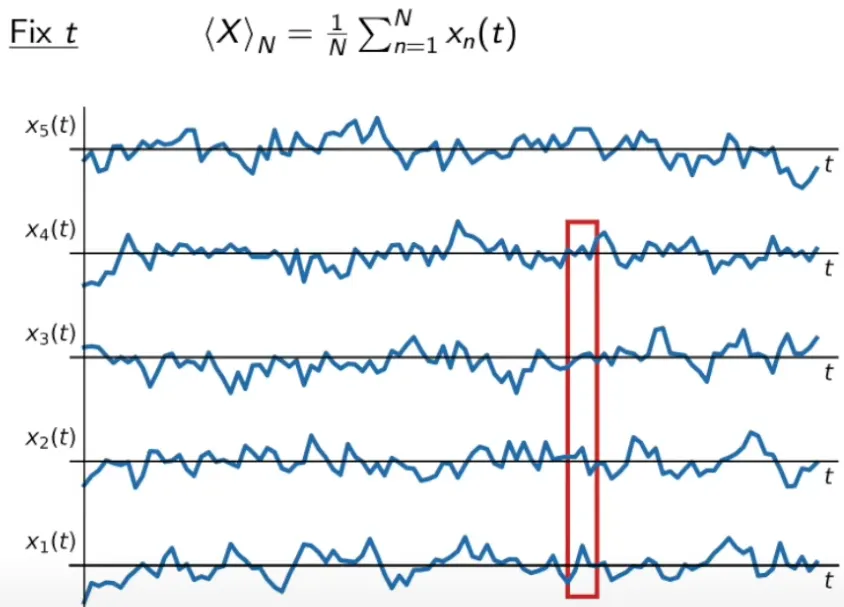
시평균(time average): 모든 시간 구간에 대한 특정 표본 함수의 평균
◦
유한 시평균(finite time average): 유한 길이의 시간 구간에 대한 시평균
◦
시평균: 시간 구간이 무한으로 발산한 경우의 표본 함수 평균
의 시평균. 무한의 시간 구간에 대한 정확한 평균은 현실적으로 얻을 수 없으나, 대략적으로 추정은 가능하다.
•
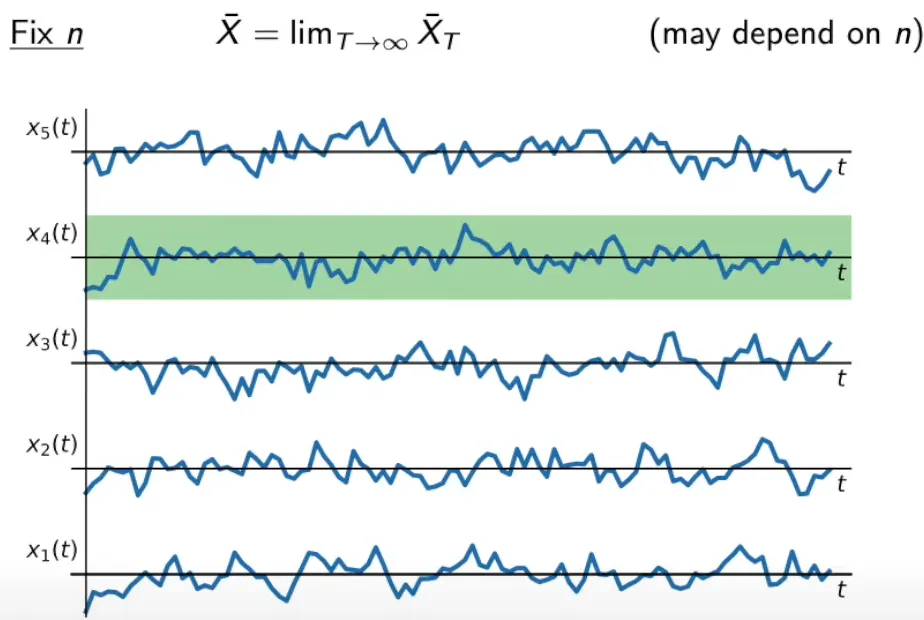
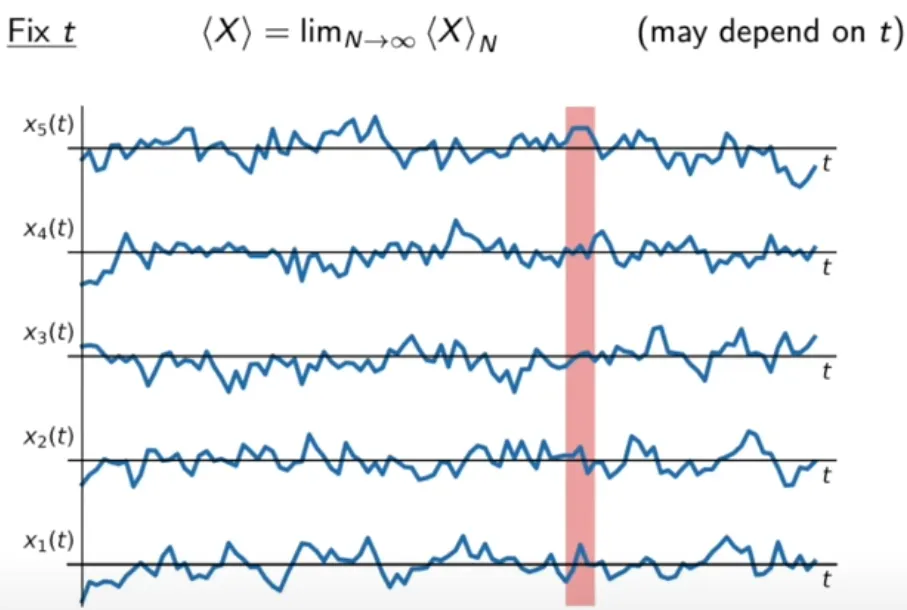
앙상블 평균(ensemble average): 가능한 모든 표본 함수들에 대해 특정 시간 단계에서 측정한 평균
◦
유한 앙상블 평균(finite ensemble average): 유한한 수의 표본 함수들에 대해 특정 시간 단계에서 계산한 평균
◦
앙상블 평균: 표본 함수의 수가 무한으로 발산한 경우의 특정 시간 단계에서의 평균
결론적으로 “확률 과정 가 Ergodic 이다”는 확률 과정의 특정 표본 함수에 대해 구해진 시평균 와 확률 과정에서 가능한 모든 표본 함수들에 대해 구해진 앙상블 평균 이 같은 것을 의미한다.
→ Ergodicity가 왜 쓸만한 시계열인지 결정하는 기준으로 활용되는 지에 대한 근거는 추후 리서치가 필요함
Ergodicity가 왜 쓸만한 시계열인지 결정하는 기준으로 활용되는 지에 대한 근거는 추후 리서치가 필요함
시계열의 길이시계열의 길이가 지나치게 짧거나 긴 경우, 추출된 일부 특징이 유효하지 않을 수 있다(예: 최대값, 최소값).
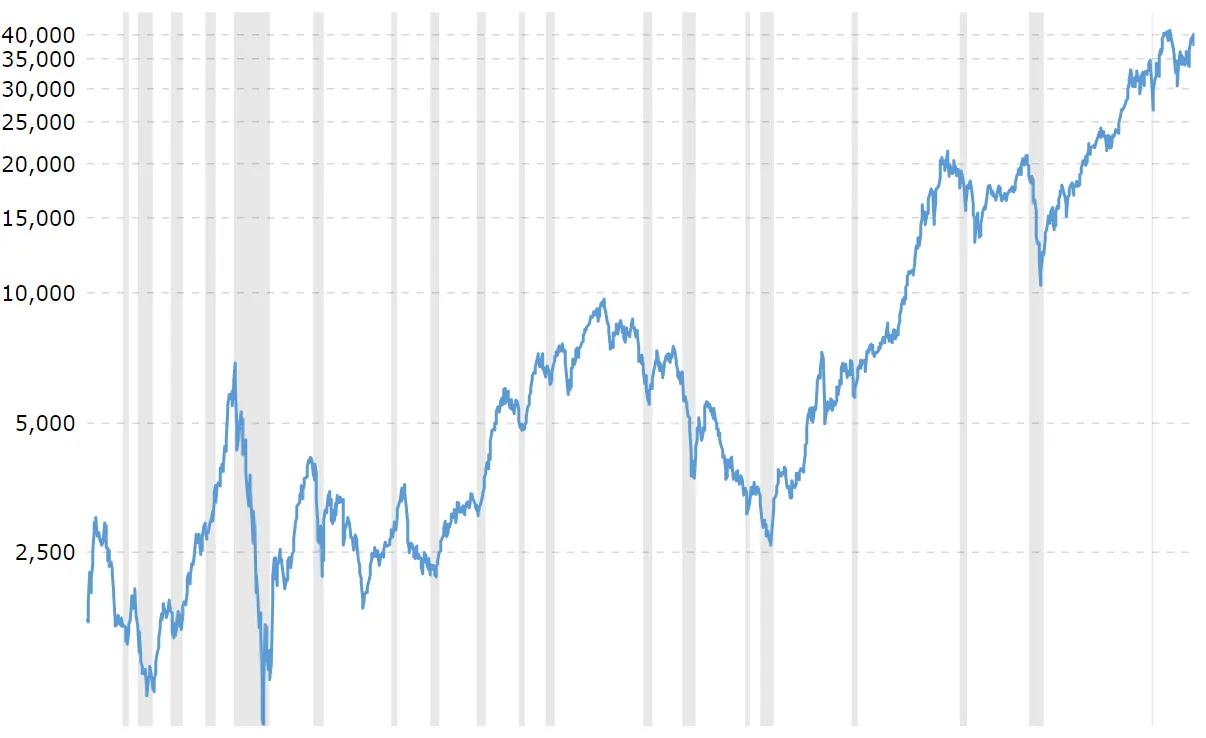
예: 다우 존스 산업평균지수(DJIA)
•
측정 기간: 1915년~
•
최대값: 39,386.35 (2024년 2월)
•
최소값: 987.67 (1932년 6월)
→ 최대값, 최소값 모두 100년이 넘는 기간 동안 측정한 DJIA 시계열을 설명하는데 유용하지 않다.
8.2.2 도메인 지식
데이터는 다양한 분야(도메인)의 시스템으로부터 취득될 수 있으며, 데이터에 대한 특징 추출 과정에서 해당 분야의 전문 지식(도메인 지식)이 자주 요구된다.
예: 금융시장 데이터
•
일별 가격 최대 변동폭 제한:
•
사이드카(sidecar): 선물(futures) 가격이 급등락할 때 일정 기간 동안 프로그램 매매를 중단시키는 제도
→ 최대 변동폭과 사이드카에 대한 도메인 지식을 통해 특정 날짜의 어떤 종목의 거래 가능한 가격 밴드(범위)에 대한 특징을 추출할 수 있다.
예: 전력 부하 데이터
•
전력 시스템 관리 측면에서 일별 평균 부하 보다 일별 최대 부하(peak load)가 더 중요하다.
8.2.3 외적 고려 사항
•
스토리지(데이터 저장) 측면
예: 데이터 정제
1.
원본 데이터 → 특징
2.
원본 데이터 삭제
예: 데이터 레이크
1.
원본 데이터 → 특징
2.
특징 삭제
•
계산 비용 측면: 특징 추출에는 코딩과 계산 과정에 비용이 소모된다. 특히, 계산 비용이 높은 추출 과정의 경우, 일부 샘플 데이터셋에 먼저 적용하고 검증이 완료된 후에 전체 데이터셋으로 확장하는 것이 좋다.
8.3 특징의 발견에 영감을 주는 장소 목록
시계열 특징 추출에는 시계열의 패턴을 합리적으로 표현하는 잘 알려진 특징들을 우선적으로 고려할 필요가 있다.
•
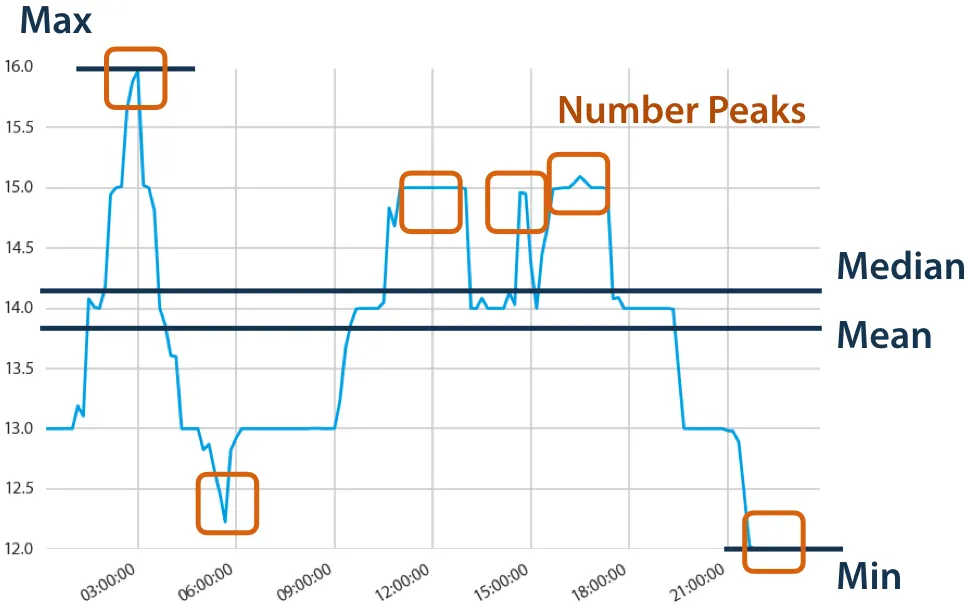
기본적인 요약 통계 특징: 평균, 분산, 최대값, 최소값, 구간 변동 등
•
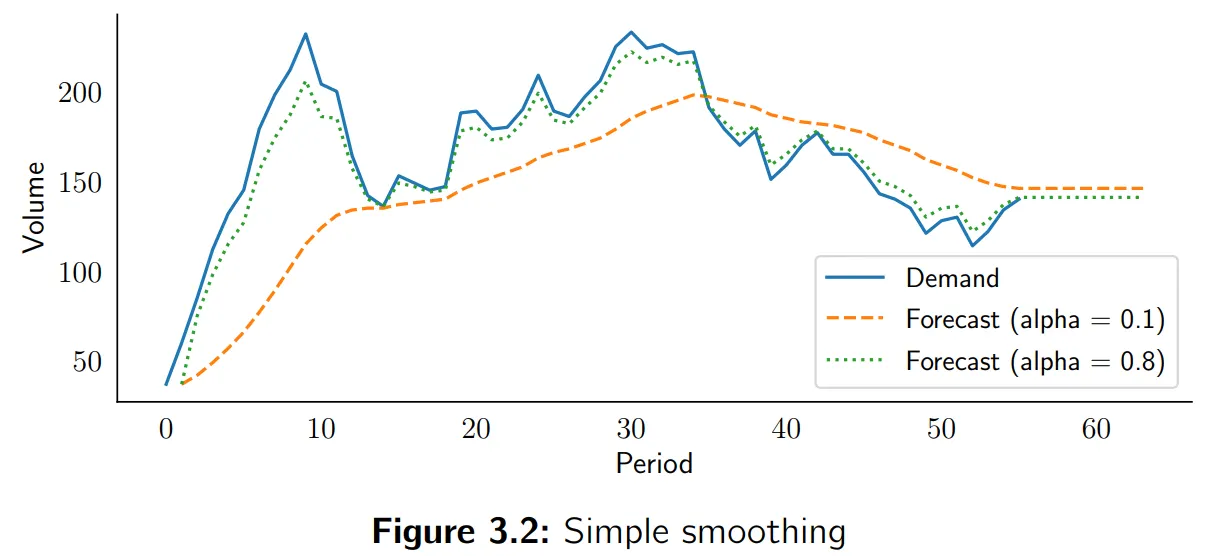
계산이 복잡하지만 일반적으로 유용한 특징: 국소적 최소값/최대값 개수, 평활 정도, 주기성과 자기상관 등
그 외의 복잡한 특징 또는 계산 비용이 높은 특징을 다루는 경우, 안정적인 동시에 효율적으로 구현된 (오픈소스) 라이브러리를 활용하는 것이 좋다.
8.3.1 시계열 특징 생성의 오픈 소스 라이브러리
파이썬의 tsfresh 패키지
tsfresh를 이용한 시계열 특징 추출 및 시각화
•
기술 통계
◦
Augmented Dickey-Fuller 검정 결과: 단위근(Unit Root) 유무를 중심으로 시계열 정상성 판별
◦
AR(k) 계수: 자기상관(Autoregressive) 모델에서 시차 k 관측치의 계수()
◦
시차 k에 대한 자기상관계수
시계열 분석 플랫폼: Cesium
•
분포 관련 특징
◦
예: 특정 구간에서 국소적 최대점(local maxima)이 몇 번 발생했는지?
◦
예: 분포 내 특정 범위에 몇 %의 데이터가 포함되어 있는지?
•
주기성 측면 특징
◦
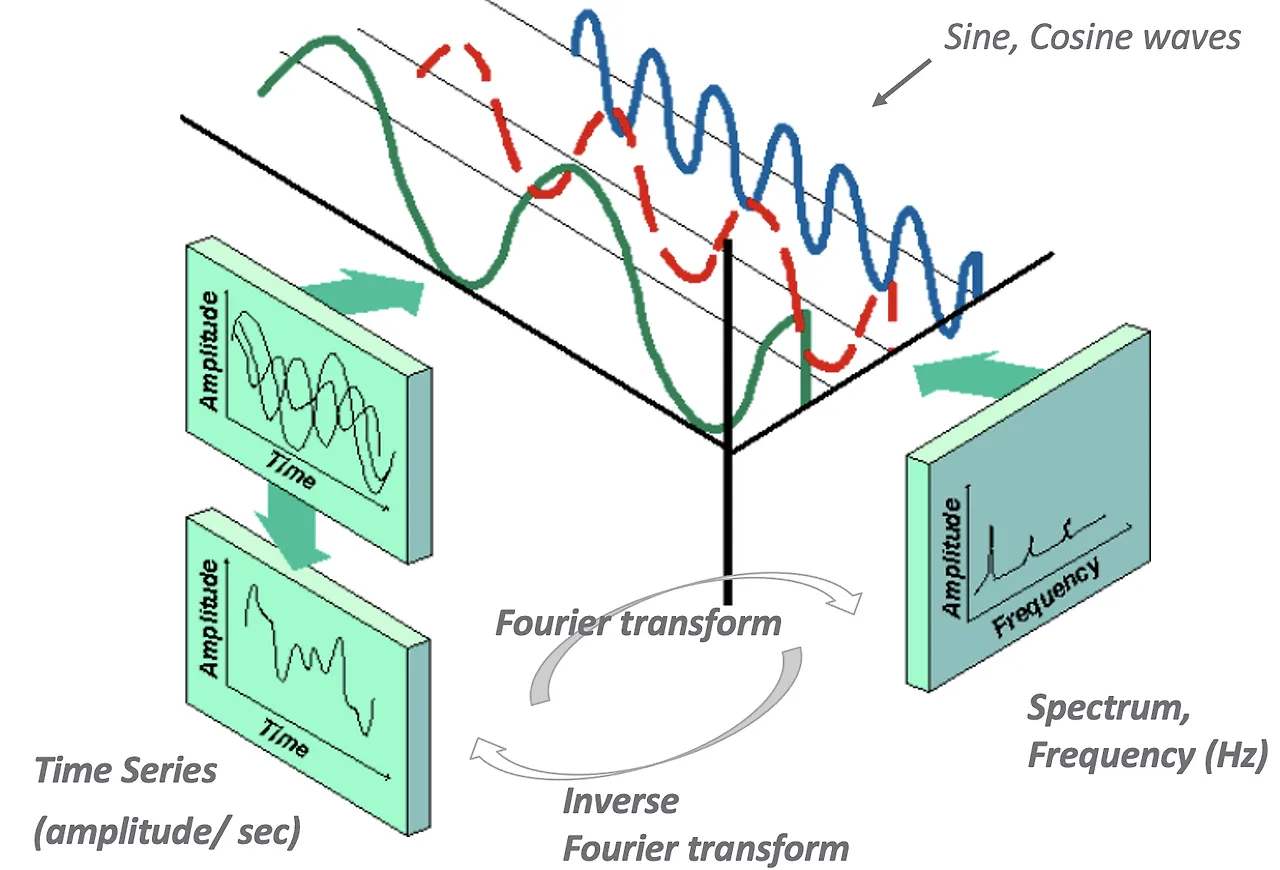
푸리에 변환: 모든 파동(시계열)은 서로 다른 주기와 진폭을 갖는 Sine 및 Cosine 함수로 표현 가능하다.
◦
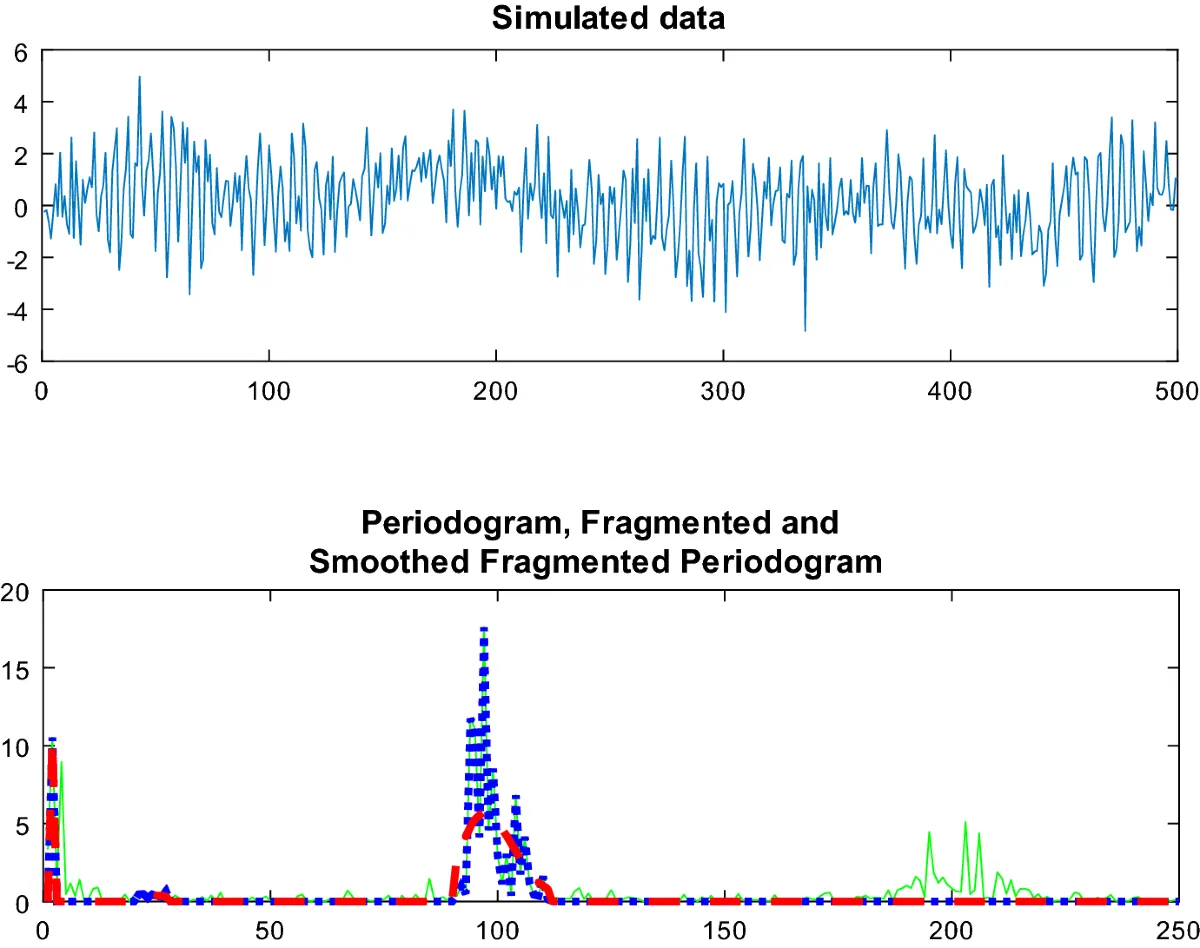
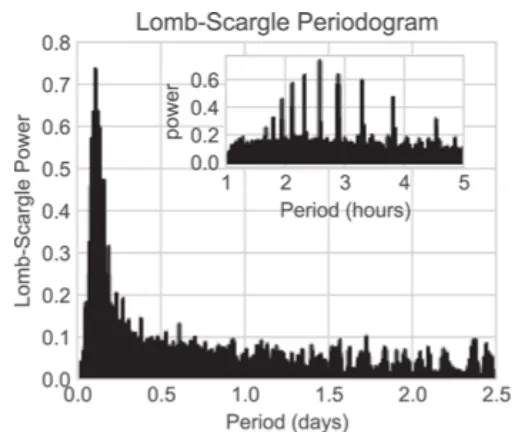
Periodogram(주기도): 스펙트럼 분석(spectral analysis)의 유형으로 신호(시계열)에 내재되어 있는 주기성(periodicity)을 분석하는 기법
푸리에 변환을 통해 신호에 대한 주기(frequency)와 강도(amplitude)를 시각화 (time domain → frequency domain)
◦
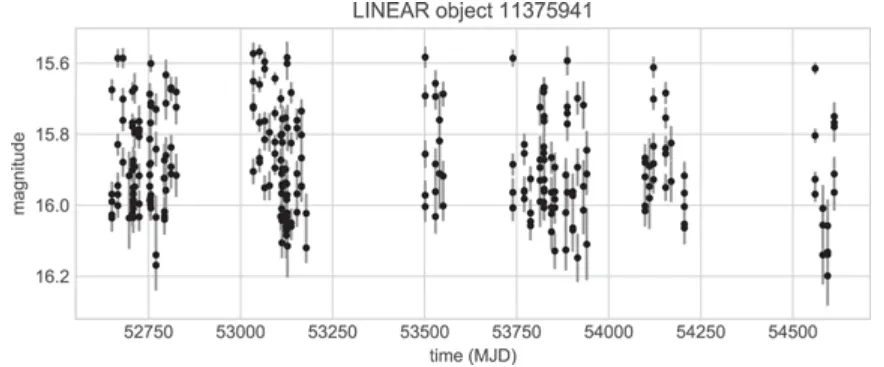
Lomb-Scargle periodogram: 불규칙적으로 측정된 시계열에 대해서 periodogram 을 계산하는 방법 → 불규칙적 이벤트 관측이 중요한 천문학에서 중요하게 활용됨
→ Cesium은 특징 추출 외에 웹 기반 GUI를 제공하므로 인터랙티브하게 시계열 분석 및 머신러닝이 가능하며, sklearn 라이브러리와의 연계도 제공한다.
R의 tsfeatures 패키지•
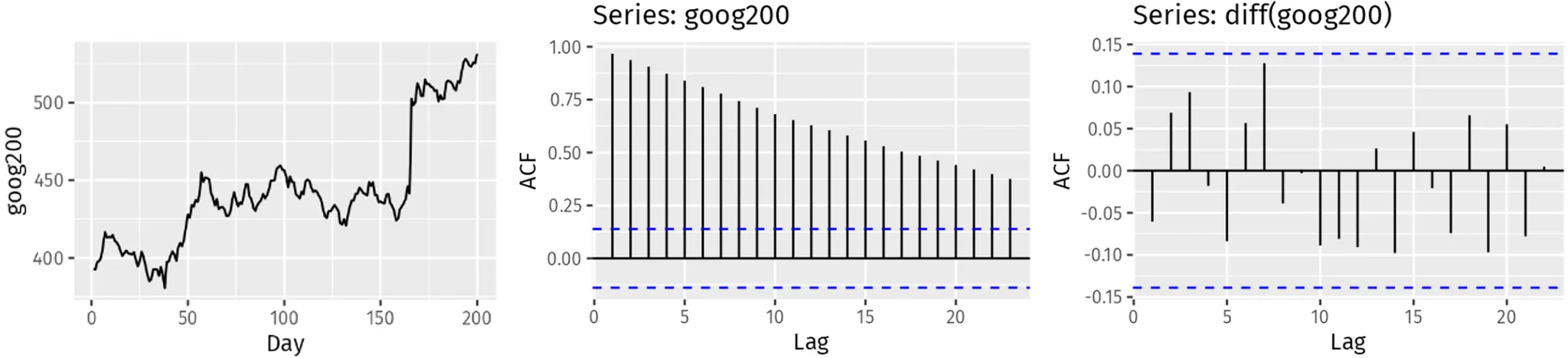
Autocorrelation plots (ACF, PACF)
•
Windowing
•
단위근 검정
8.3.2 특정 도메인의 특화된 특징의 예
금융 또는 헬스케어와 같이 특정 도메인에 특화된 특징들은 해당 분야의 데이터를 분석할 때 유용한 인사인트를 제공한다. 그러므로, 새로운 영역에서 데이터 분석을 시작할 때는 해당 분야에서 널리 알려진 특징들을 우선적으로 검토할 필요가 있다.
주식시장의 기술지표•
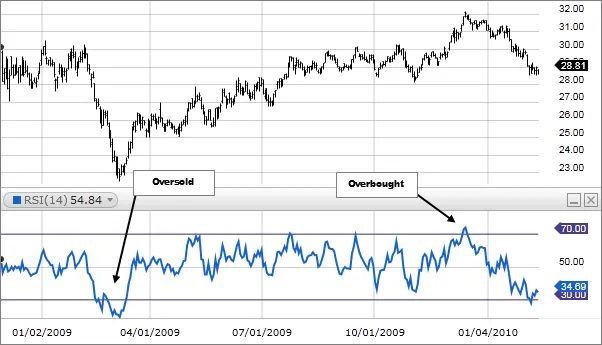
상대강도지수(RSI: Relative Strength Index): 일정 기간 동안 주가가 전일 가격에 비해 상승한 변화량과 하락한 변화량의 평균값
◦
상승 변화량이 크면 → 과매수
◦
하락 변화량이 크면 → 과매도
◦
일반적으로 RSI가 70 이상에서 하락하거나, 30 이하에서 상승하면 매매신호로 판단
•
이동평균 수렴발산(MACD: Moving Average Convergence Divergence): 단기간 이동 평균과 장기간 이동평균 과의 차이를 나타내는 지표로서, 매수/매도 신호 판단에 활용됨
•
체이킨 머니 플로우(CMF: Chaikin Money Flow): 종목 가격과 거래량을 결합하여 들어오고 나가는 자금 흐름을 정량화하는 지표로서 추세 강도 및 반전을 예측할 때 활용됨
헬스케어 시계열•
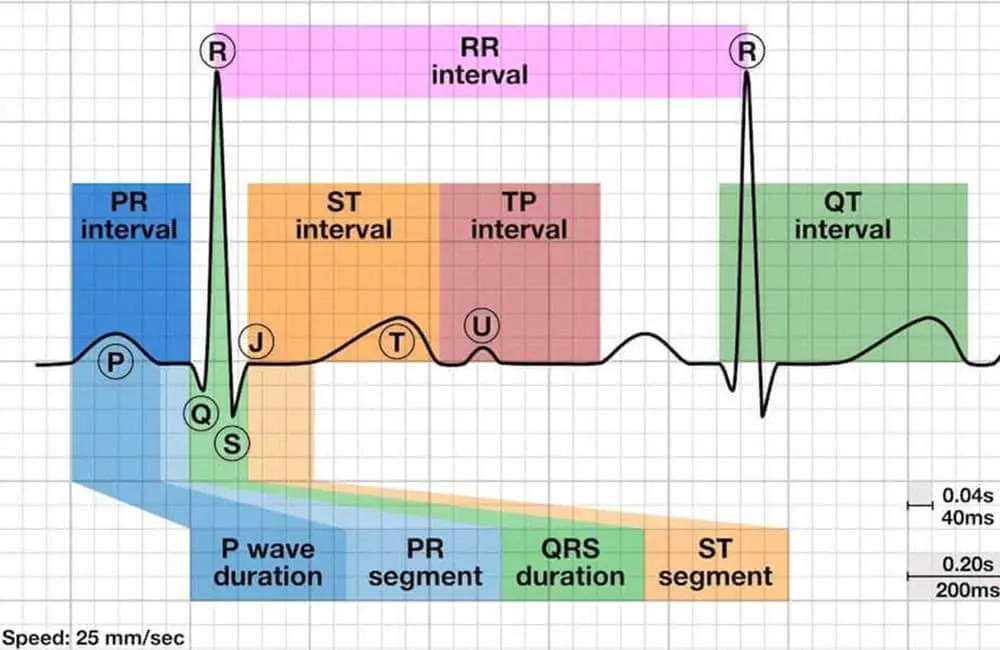
심전도(EKG: Electrokardiogram) 데이터: 심장의 전기적 흐름을 측정한 데이터로서 심장의 동작에 따라 반복적으로 발생하는 주요 패턴(wave, interval)에 대한 특징을 통해 부정맥 및 심근경색 등의 이상 증세를 분석할 수 있음
◦
P wave : 심방의 수축 (심방 탈분극)
◦
QRS wave : 심실의 수축 (심실 탈분극)
◦
T wave : 심실의 이완
◦
PR interval : 심방 수축 시작 ~ 심실 수축 시작
◦
ST interval : 심실 수축 이후 ~ 심실 이완 시작
◦
QT interval : 심실 수축 시작 ~ 심실 이완 끝
8.4 생성된 특징들 중 일부를 선택하는 방법
개인이 수동적으로 검토하기에는 많은 수의 특징들이 생성되었다면? → 자동화된 방식의 특징 선택 방법이 필요하다.
FRESHFRESH(FeatuRe Extraction based on Scalable Hypothesis test)는 특징 별 p-value를 기반으로 중요도를 평가하는 방식이다. 벤자민-예쿠티에리 절차(Benjamini-Yekutieli procedure)라는 어려운 이름의 방법(실제로도 복잡함 )을 통해 p-value를 평가하는 데, 이 과정의 계산 비용이 높기 때문에 FRESH는 병렬 계산이 용이하도록 설계되어 있다.
)을 통해 p-value를 평가하는 데, 이 과정의 계산 비용이 높기 때문에 FRESH는 병렬 계산이 용이하도록 설계되어 있다.•
라이브러리 예: tsfresh.examples.robot_execution_failures.load_robot_execution_failures( )
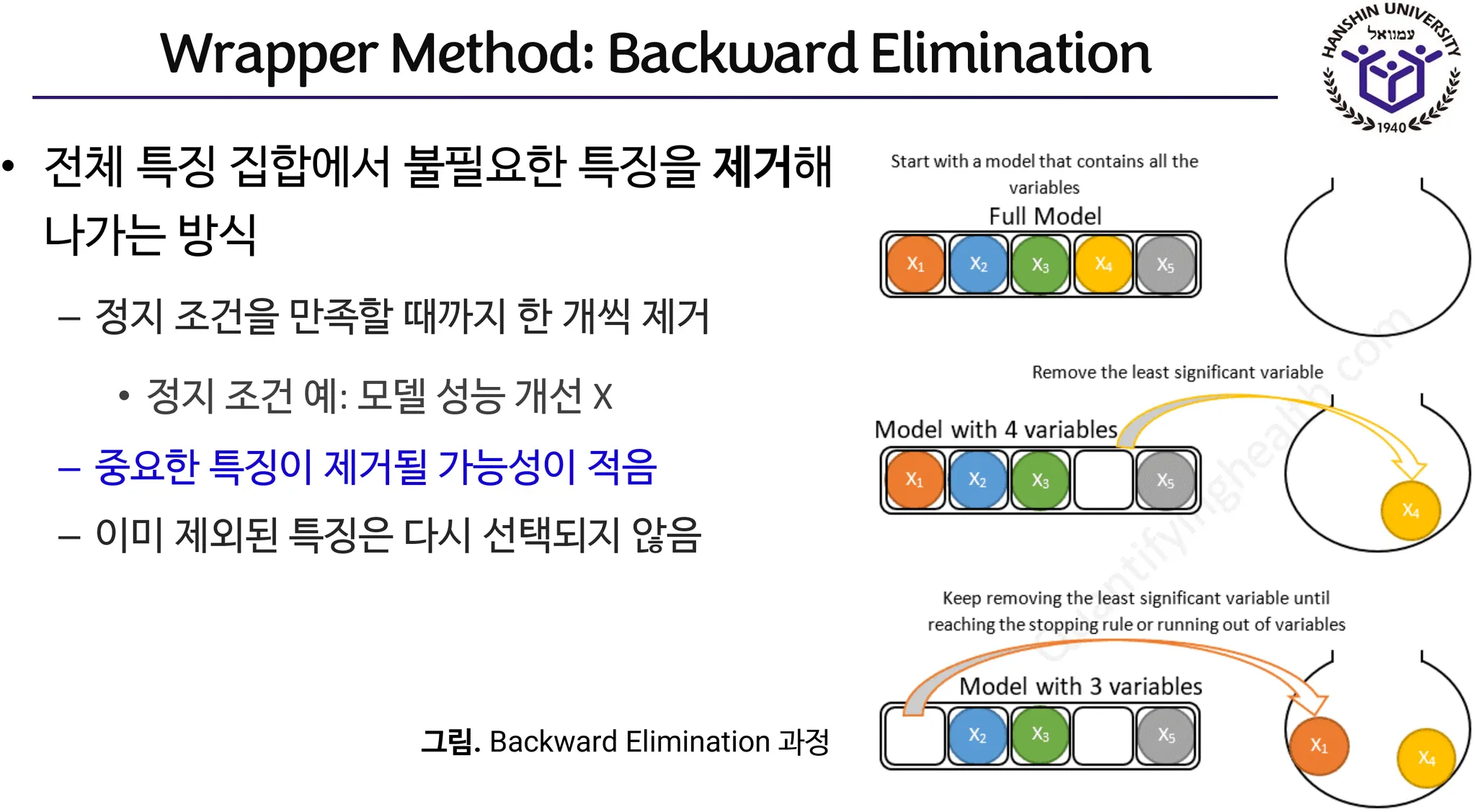
RFE(재귀특징제거법)RFE(Recursive Feature Elimination)는 전체 특징 집합에서 점진적으로 특징을 제거하고 모델 성능을 측정하는 과정을 반복적으로 수행하는 방법으로 Backward Selection 의 일종이다.
•
라이브러리 예: sklearn.feature_selection.RFE
RFE의 개념(데이터엔지니어링[NI247] 강의 노트)
마무리
8장에서는 원본 시계열 데이터를 적은 수의 정보로 효율적으로 표현하기 위한 특징 추출에 대하여 다뤘다. 특징 추출을 수행하는 대표적인 이유는 다음과 같다.
•
시계열 특성을 반영한 전반적인 요약을 통해 데이터에 대한 이해도
•
머신러닝 알고리즘이 요구하는 형태의 학습 데이터를 구성
◦
(추출된) 좋은 특징은 모델 학습의 효율성을 높일 수 있다.
•
원본 시계열을 적은 수의 정량적 지표로 압축 → 원본 시계열을 유지할 필요성 X
이와 관련하여 시계열 데이터의 대표적인 특징들을 살펴보았고, 특징 추출을 자동화하기 위해 널리 알려진 특징 추출 라이브러리(tsfresh, Cesium, tsfeatures)들을 소개하였다. 이러한 라이브러리를 이용하면 시계열로부터 수 천개 이상의 특징들을 손쉽게 생성할 수 있다는 장점이 있다.
반면에, 생성된 모든 특징들이 유용하지 않을 수 있으므로, 특징 선택 과정을 통해 본격적인 데이터 분석 및 모델링에 사용되는 최종 데이터셋을 선별해야 한다. 8장에서는 대표적인 특징 선택 방법인 FRESH와 RFE에 대해서 소개하였다.
참고문헌
•
•
•
•
•
(VanderPlas 18) Understanding the Lomb-Scargle Periodogram, The Astrophysical Journal
•
•
