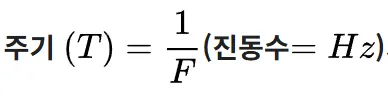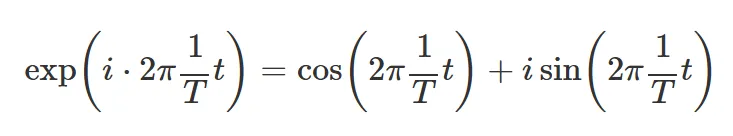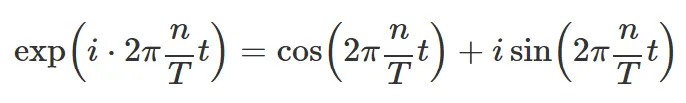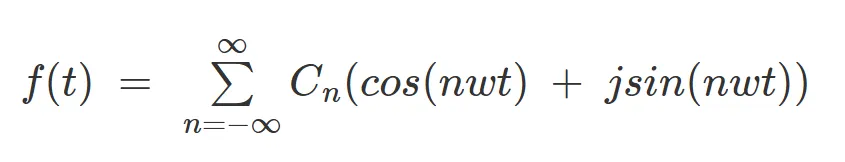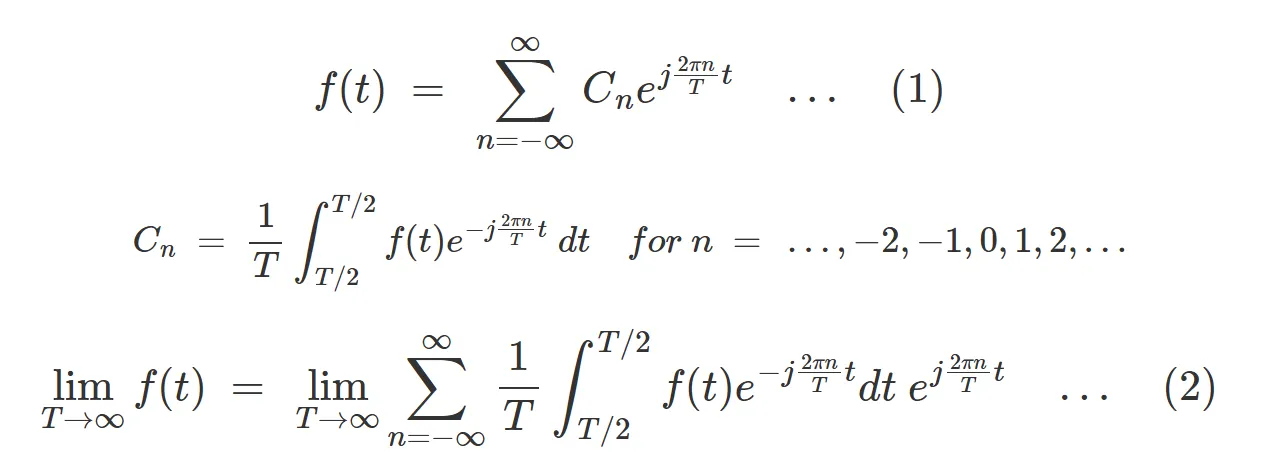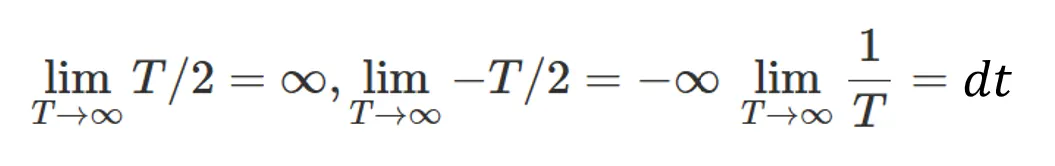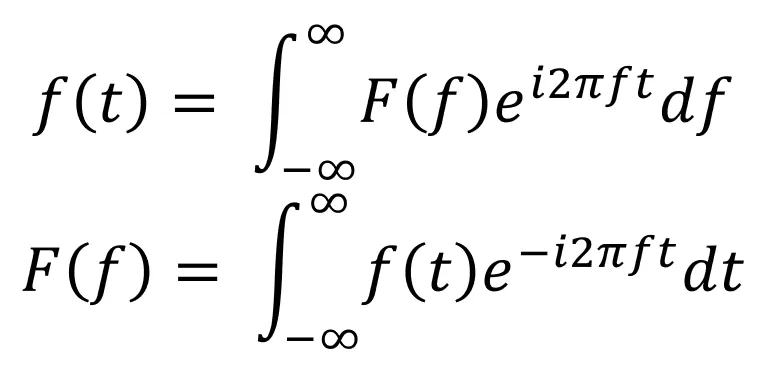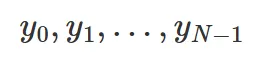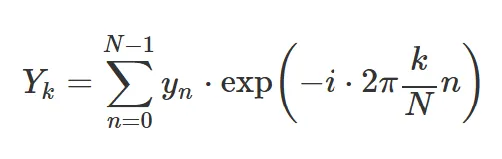1. 푸리에 변환 (Fourier Transform)
1.1 정현파 신호
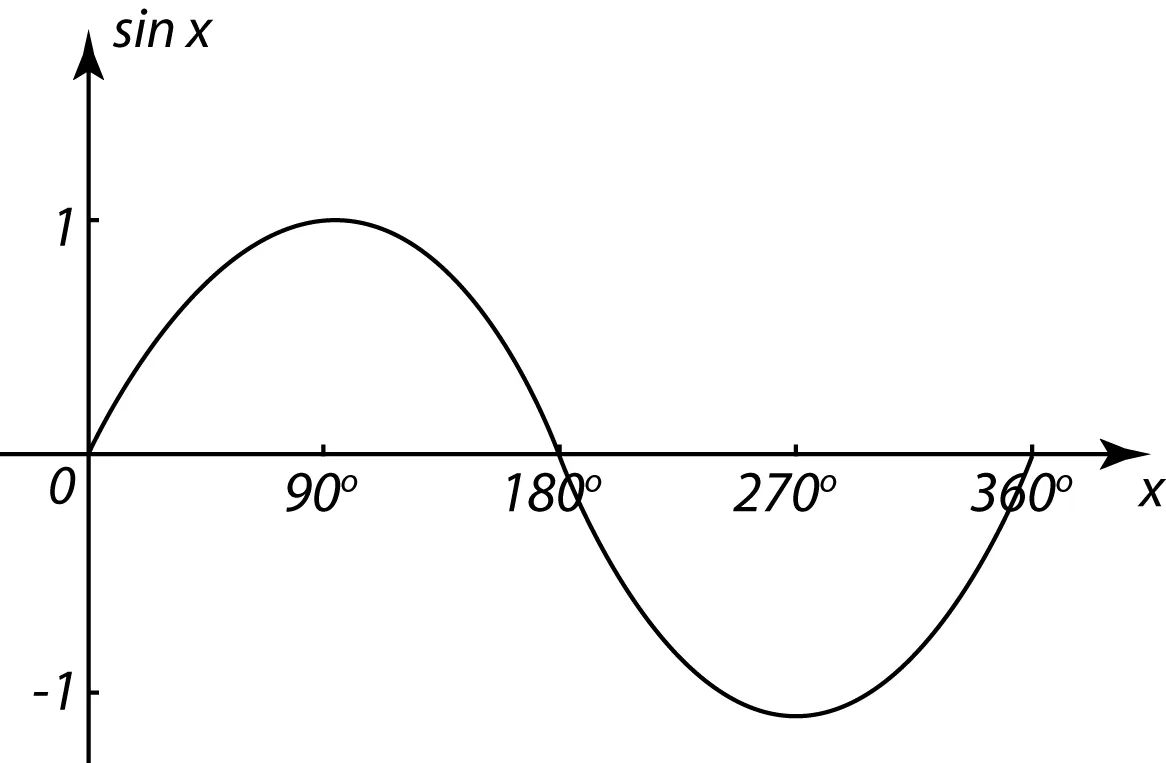
→ 주기 신호 ( 사인 함수의 기하학적 그래프 )
•
주기(period) : 일정한 시간마다 같은 현상이 이루어지는 것
◦
주기 함수에서 정의역의 모든 원소 x에 대해 f(x+a)=f(x)인 가장 작은 양수 a
•
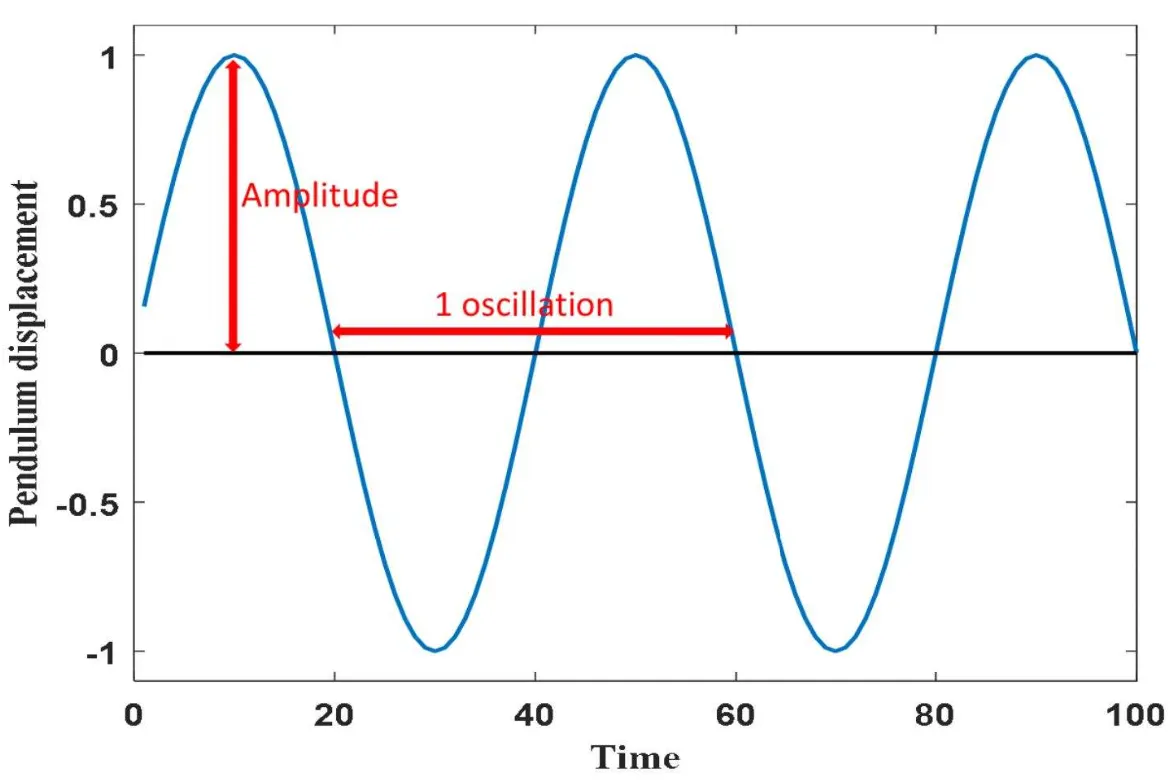
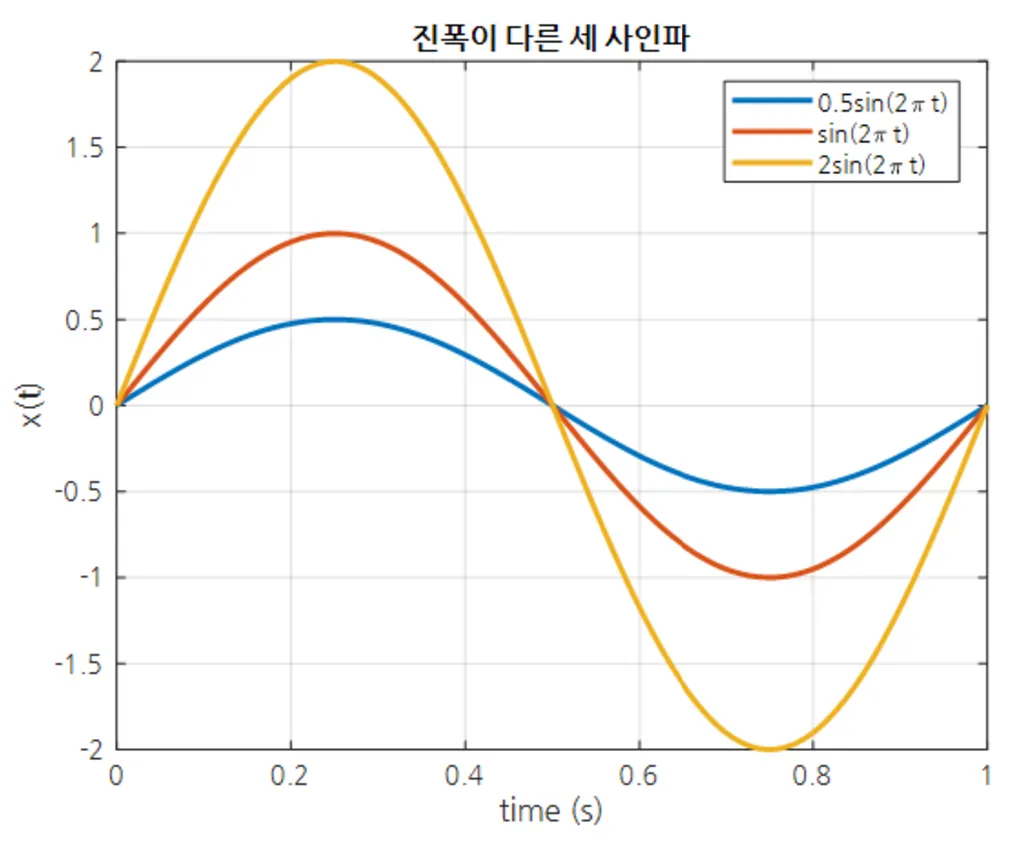
진폭(amplitude) : 주기적으로 진동하는 파의 진동 폭
•
진동(oscillation) : 주기가 있는 변
1.2 주기와 주파수
•
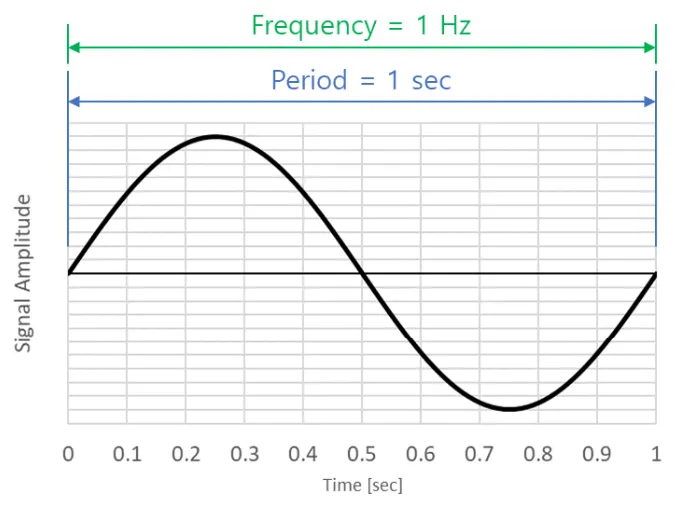
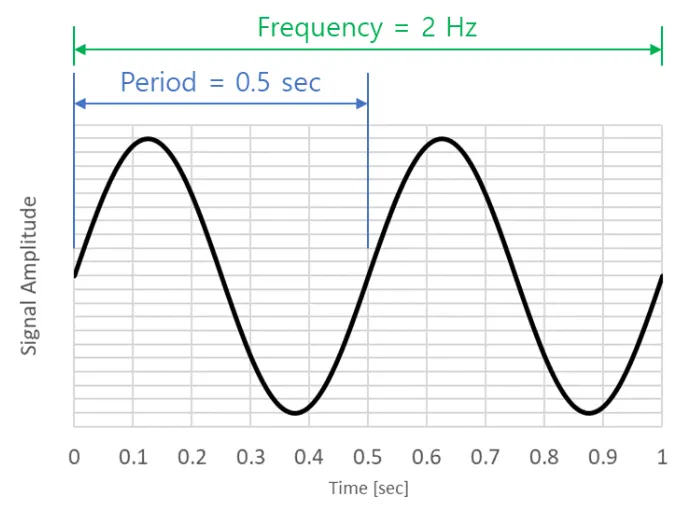
주기(period) : 일정한 시간마다 같은 현상이 이루어지는 것
•
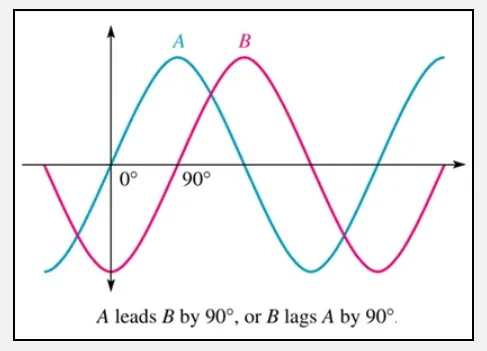
위상(phase) : 주기 함수의 시작 지점을 기준으로 얼마나 이동했는 지를 뜻함
•
크기(magnitude) 변화 :
•
주파수(frequency, Hz) : 주기적인 현상이 단위시간 동안 몇 번 일어났는 지를 뜻함
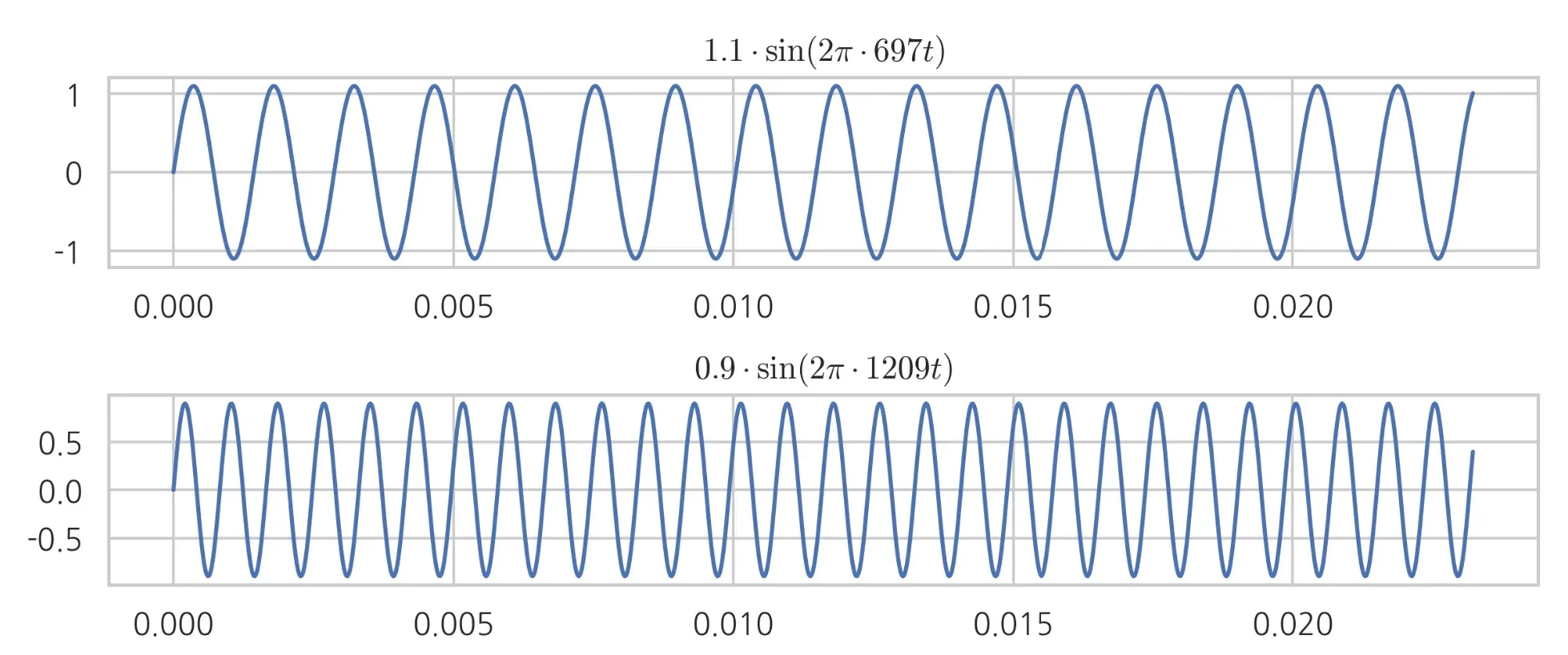
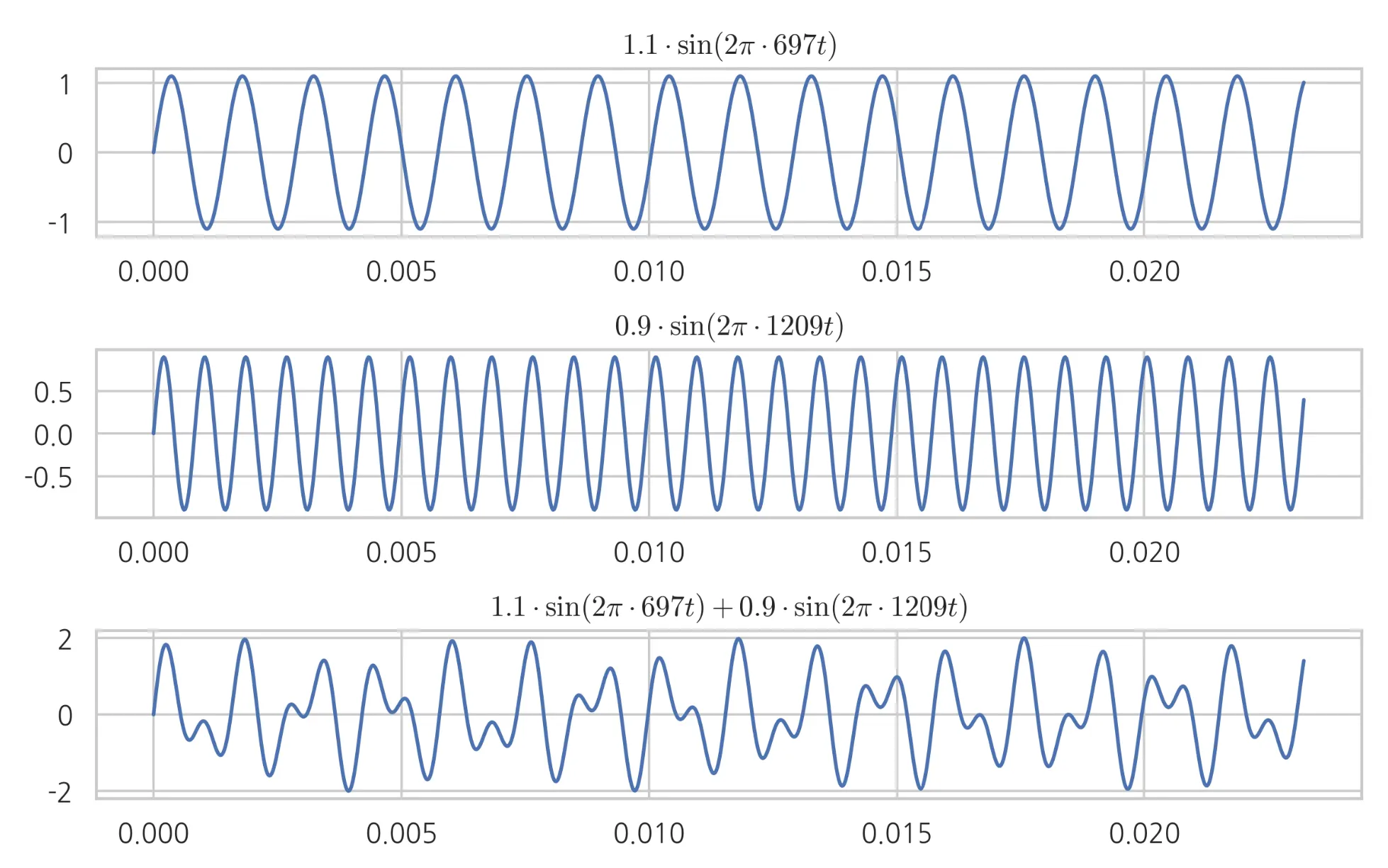
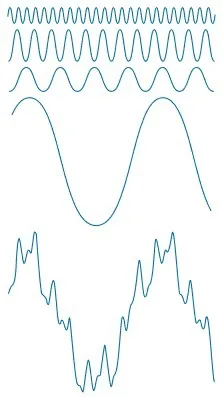
1.3 정현파 조합
→ 모든 신호는 주파수와 크기, 위상이 다른 정현파의 조합으로 나타낼 수 있음.
1.4 복소 지수함수
→ 코사인 함수인 실수부와 사인 함수인 허수부의 합.
•
주기가 , 주파수가 인 복수 지수 함수
•
주기가 , 주파수가 인 복수 지수 함수
1.5 푸리에 급수
•
시간 주기마다 반복하는 함수를 주기 함수. 푸리에 급수를 통해 코사인과 사인 함수로 이루어진 주기 함수를 표현할 수 있음.
•
급수 : 수열의 모든 항을 더한 것, 수열의 합.
•
아무리 복잡한 함수라도 그것이 주기를 가진다면 단순한 파동들의 조합을 합하여 표현할 수 있음.
•
무한하게 다양한 주파수를 가진 정현파를 각각 얼마나 가중해서 더해주느냐에 따라 모든 복잡한 주기함수를 표현할 수 있음.
1.6 푸리에 변환
→ 조합된 정현파의 합 신호에서 그 신호를 구성하는 정현파들을 각각 분리해내는 방법.
→ 주기 를 가지고 반복되는 모든 함수 는 주파수와 진폭이 다른 몇개의 사인 함수(정확히는 복수 지수함수)의 합으로 나타냄. 이 사인 함수의 진폭을 구하는 과정이 푸리에 변환.
•
비주기 함수도 푸리에 급수를 이용하여 주파수 영역에서 분석할 수 있을까?
◦
시간 주기(T)가 무한히 크다면?
◦
비주기 함수 = 시간 주기(T)가 무한히 큰 주기함수
•
(1) 푸리에 급수(Fourier Series), 주기함수()를 대상으로 함.
•
(2) 양쪽의 를 무한으로 보냄.
•
이기 때문에 매우 작은 값이라는 의미로 로 표기.
•
수식 (2)를 정리함. (로 치환.)
2. 이산 푸리에 변환 (Discrete Fourier Transform, DFT)
•
이산적인 입력 신호에 대한 푸리에 변환.
•
고속 푸리에 변환(Fast Fourier Transform, FFT)을 이용해 빠르게 계산할 수 있음.
•
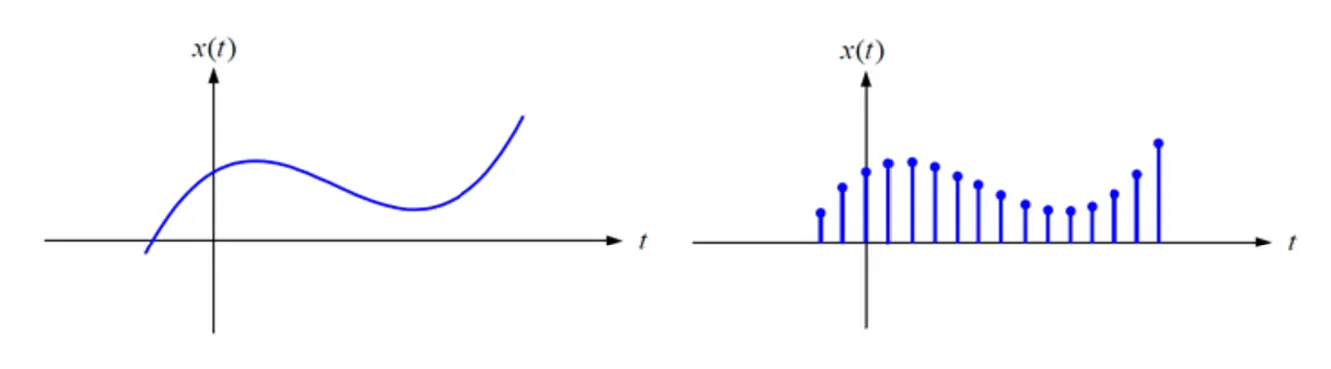
어떤 아날로그 신호에 대해서 연속된 시간으로 값을 측정할 수 없는 현실적인 이유.
•
따라서 주파수에 대해서도 연속된 것이 아닌, 간격이 존재하는 이산 주파수의 형태로 다뤄야 함.
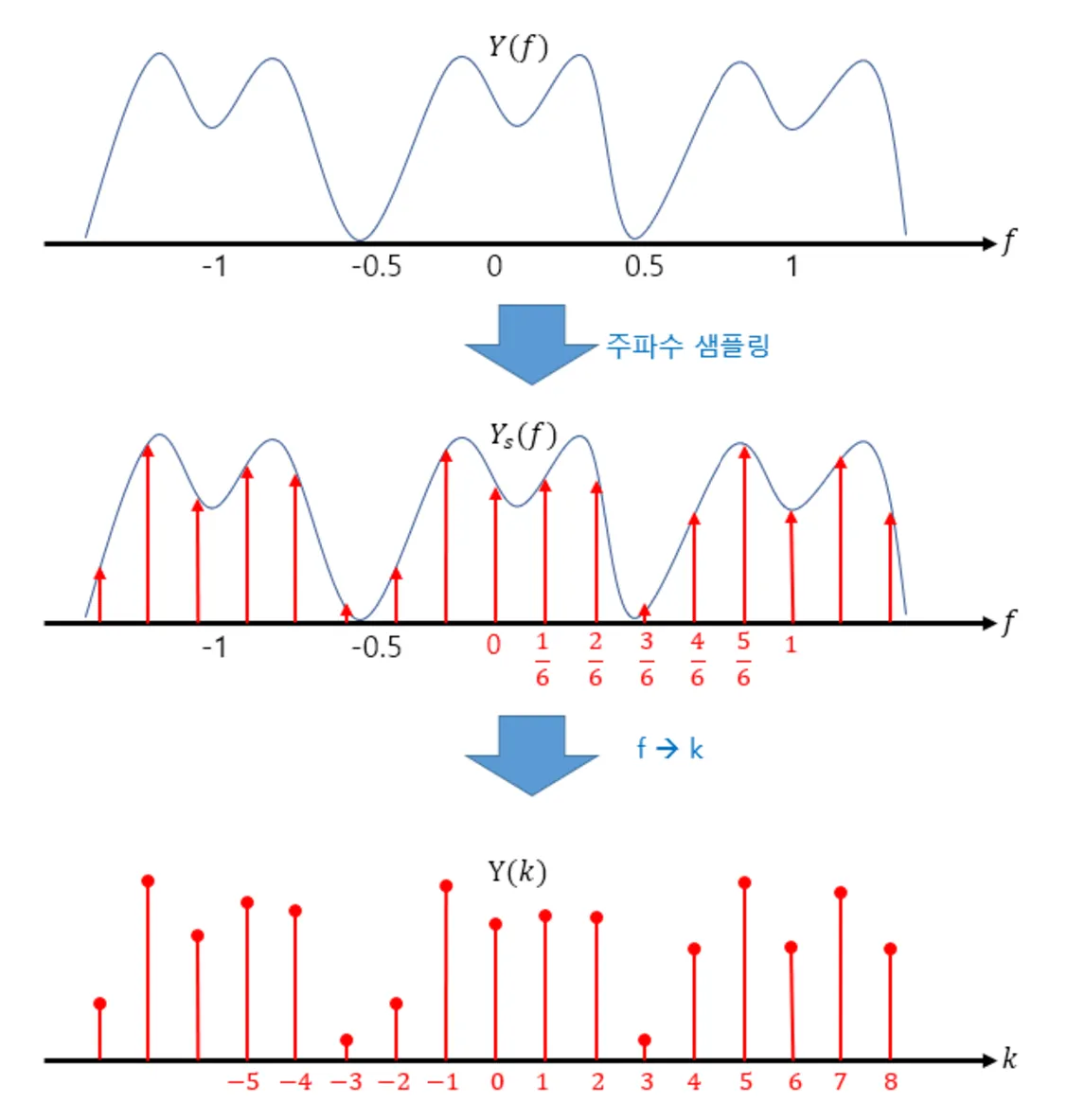
•
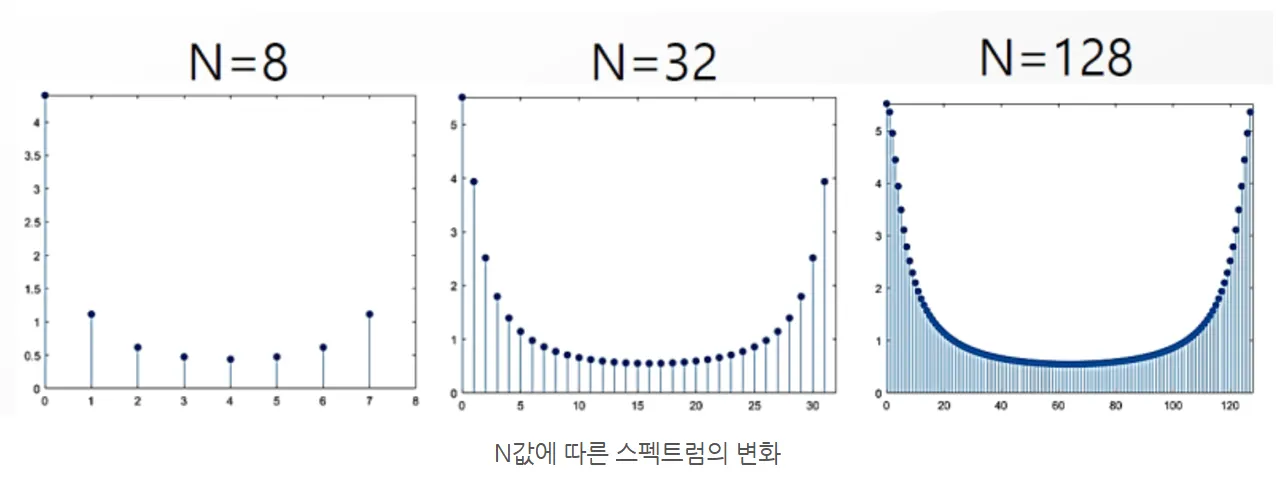
위 그림은 주파수 사이를 1/6 간격으로 샘플링하는 것을 보여줌.
•
주파수 인 지점에서만 값을 가지는 신호가 됨. (k: 정수)
•
주파수 f에 의한 함수 Y(f)가, 정수값 k에 의한 함수 Y(k)로 변경되게 됨.
•
→ 주파수 공간에서 이산 간격으로 샘플링된 신호에 대한 푸리에 변환.
•
길이가 인 이산시간 시계열 데이터가 있을때 이 시계열이 주기 을 계속 반복된다고 가정하여 푸리에 변환.
→ 이산시간 시계열 데이터
•
이때 진폭 를 원래의 시계열 데이터에 대한 푸리에 변환값.
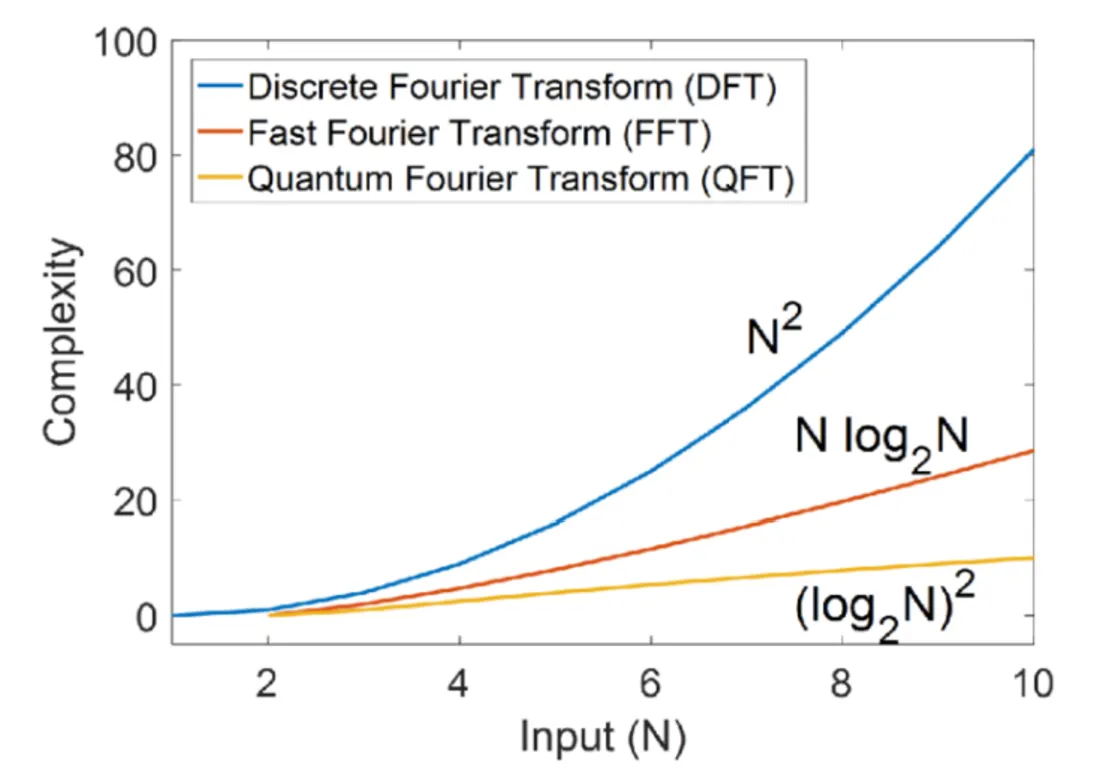
3. 고속 푸리에 변환 (Fast Fourier Transform, FFT)
•
아주 적은 계산량으로 DFT를 하는 알고리즘.
•
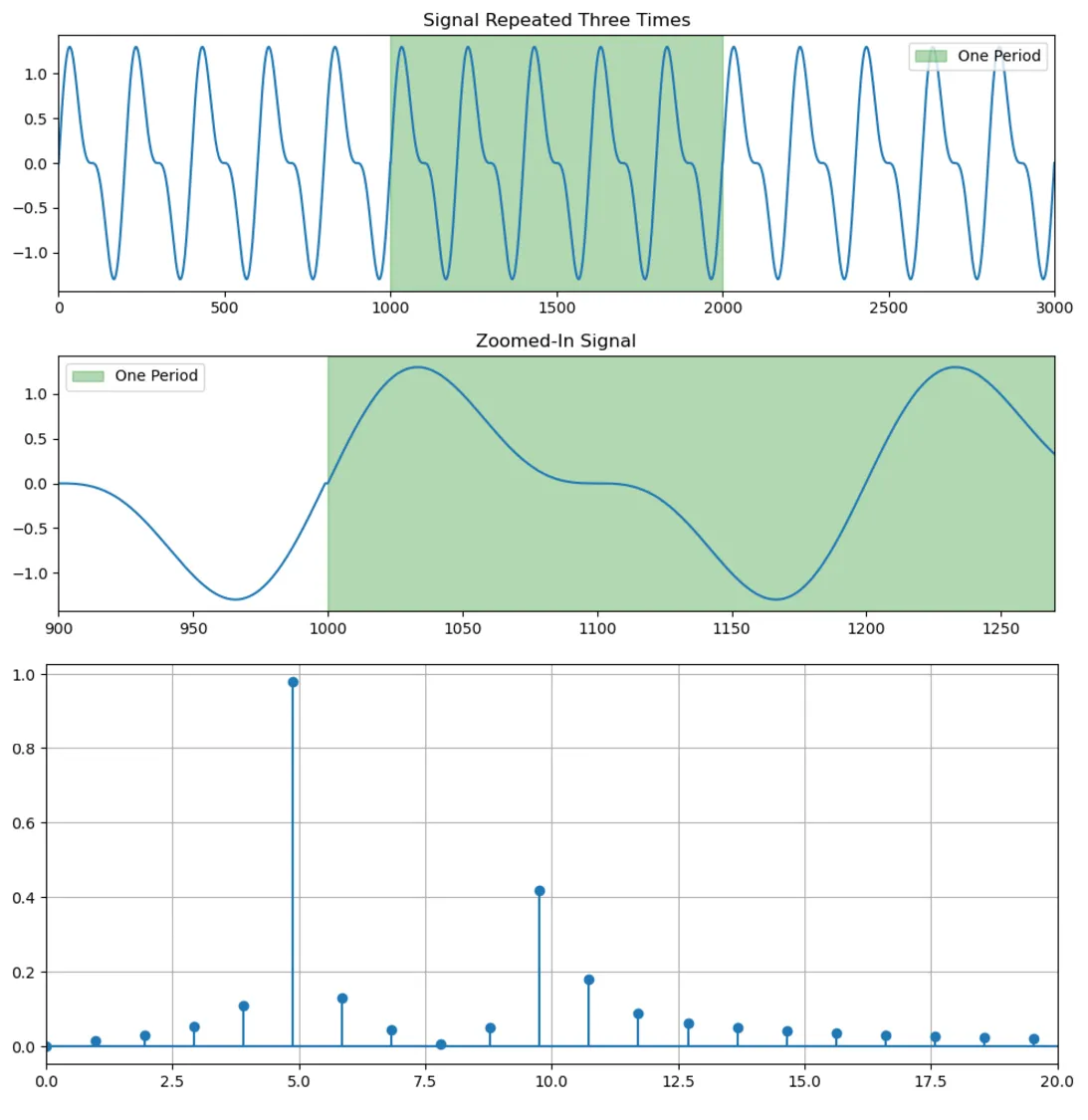
아래와 같이 계속 반복되는 시계열에 대해 푸리에 변환을 하는 것.
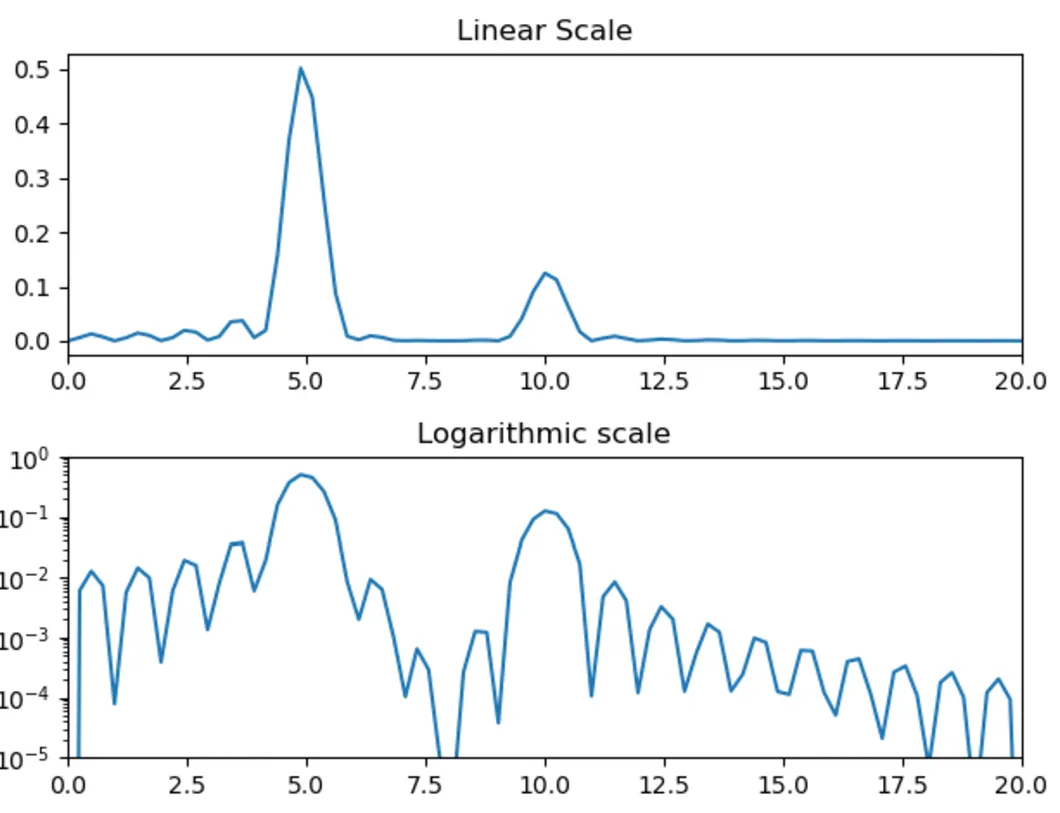
이산 시계열 데이터 및 FFT 결과 그래프 생성 코드
•
5Hz와 10Hz 성분이 강하게 나타나는 것을 볼 수 있음.
y = np.sin(5 * 2.0 * np.pi * x) + 0.5 * np.sin(10 * 2.0 * np.pi * x)
4. 스펙트럼 (Spectrum)
•
푸리에 변환은 시계열 데이터를 주파수 영역으로 변환하는 것을 말하지만 스펙트럼(spectrum)은 확률론적인 확룰과정 모형을 주파수 영역으로 변환하는 것을 말함.
•
아래는 전체 시계열을 짧은 구간으로 나눈 뒤 깁스 현상을 줄이기 위해 각 구간에 윈도우를 씌우고 FFT 계산으로 나온 값을 평균하는 방법.
이산 시계열 데이터 및 FFT 결과 그래프 생성 코드
•
FFT : 신호를 시간 영역에서 주파수 영역으로 변환 알고리즘
◦
예를 들어 음악 신호를 분석한다고 하면, 어떤 악기 소리가 주파수에서 지배적인지 확인하는 데 유용.
•
(파워) 스펙트럼 : 주파수 성분의 진폭(혹은 에너지)을 나타내는 그래프
◦
동일한 음악 신호를 다룰 때, 특정 주파수 대역(저음, 중음, 고음)에서의 전체적인 부포를 보여줌.
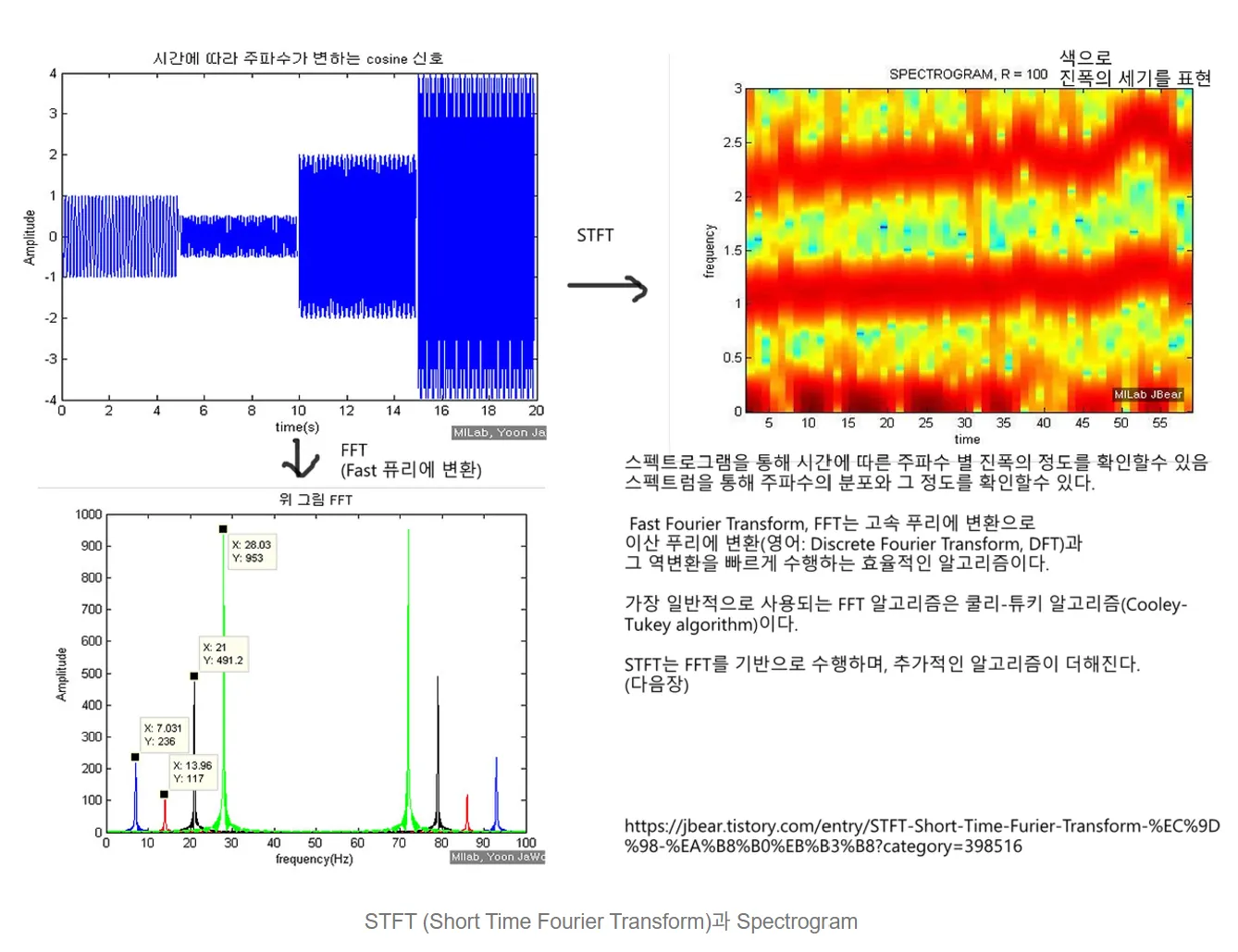
5. STFT(Short-Time Fourier Transform)
•
주파수 특성이 시간에 따라 달라지는 사운드를 분석하기 위한 방법
•
FFT를 쓰지만 시간의 개념이 추가된 것.
•
시계열을 일정한 시간 구간으로 나누고 각 구간에 대해 스펙트럼을 구한 데이터.
•
시간-주파수 2차원 데이터
6. 코드 구현 및 데모
•
파이썬으로 STFT 스펙트럼 분석을 하려면 librosa 패키지를 사용해야 함.
•
https://pixabay.com/ko/music/search/루프/ 사이트에서 mp3를 받고 wav로 변환.
•
음원 이름 : 在りし日 During_one's_lifetime.mpe
import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plt
# Load the WAV file
y, sr = librosa.load('test.wav', sr=None) // sr : 샘플링 주파수 (초당 샘플 개수)
# Short-Time Fourier Transform (STFT) 실행
D = np.abs(librosa.stft(y))
# 진폭을 데시벨로 변환
db_D = librosa.amplitude_to_db(D, ref=np.max)
# 스펙트로그램 시각화
plt.figure(figsize=(10, 6))
librosa.display.specshow(db_D, y_axis='log', x_axis='time')
plt.xlim(0, 48)
plt.title('STFT of test.wav')
plt.colorbar(format='%+2.0f dB')
plt.show()
Python
복사
•
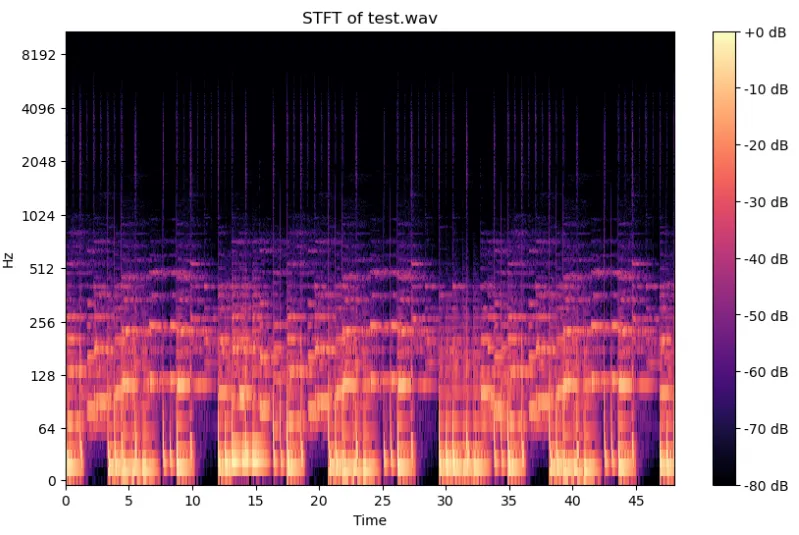
이 그래프는 오디오 신호의 시간-주파수 특성을 보여줌.
•
그래프의 색상은 진폭을 나타냄. 진폭이 큰 부분은 노란색이나 빨간색으로 표시되고, 진폭이 작은 부분은 보라색 등으로 표시됨. 즉, 붉은 영역은 해당 시간과 주파수에서 강한 신호가 있음을 의미.
•
주파수 대역에 따라 신호의 강도가 어떻게 변화하는 지 확인.
•
저주파수에서는 베이스나 저음 소리가 강하게 나타나고, 고주파수에서는 피아노나 심벌즈와 같은 고음 성분이 주로 나타남.
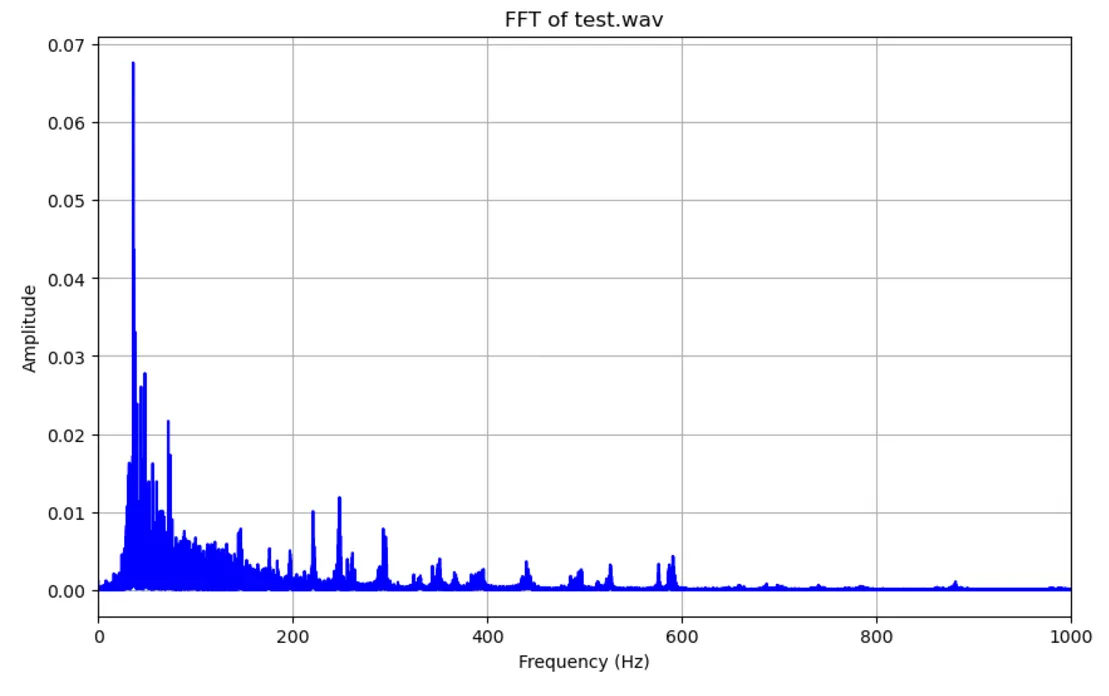
# FFT 계산
N = len(y) # 신호의 길이
T = 1 / sr # 샘플링 간격
f = np.linspace(0, sr / 2, N // 2) # 단면 주파수 축 생성 (0~sr/2 범위에서 N/2개의 균등하게 분포된 값)
# FFT 실행 및 단면 스펙트럼 계산
Y = np.fft.fft(y)
amplitude = 2 / N * np.abs(Y[:N // 2]) # 진폭 스펙트럼 ( 2/N : 진폭 단위에 맞게 정규화)
# FFT 결과 시각화
plt.figure(figsize=(10, 6))
plt.plot(f, amplitude, color='blue')
plt.title('FFT of test.wav')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.xlim(0, 1000)
plt.grid()
plt.show()
Python
복사