4.1 시계열 시뮬레이션의 특별한 점
시뮬레이션(Simulation)
실제로 테스트 해보기 어려운 초대형 프로젝트나 위험한 테스트 등을 모의실험 해보는 것
⇒ 시계열에서는 특정 시간에 발생 가능한 일을 예측하기 위해 사용
•
서로 다른 시간에 발생하는 데이터를 정확히 비교하기 어려움
◦
e.g.) 하나의 시계열은 2021-2022년까지의 데이터를, 다른 하나는 2022-2023년까지의 데이터를 가지는 경우(시간적 불일치, 계절성 및 주기성의 영향을 받음)
•
간단한 시뮬레이션은 확률 보행(Random work)과 같은 합성 데이터로 얻을 수 있음
•
시계열 시뮬레이션은 계산적 부담이 큰 분야에서 많이 활용됨
◦
기상학(meteorology), 금융학(finance), 전염병학(epidemiology), 양자화학(quantum chemistry), 플라즈마 물리학(plasma physics)
시뮬레이션과 예측
•
시뮬레이션과 예측은 둘 다 시스템의 유동성과 파라미터에 대한 가설을 세운 후 가설을 기반으로 생성될 데이터 추론하는 것으로 유사
•
정성적 관측은 예측보다 시뮬레이션에 통합하는 것이 더 쉬울 수 있음
•
시뮬레이션은 확장 가능한 형태로 실행되므로 여러 시나리오를 관찰 가능하지만 예측은 시뮬레이션보다 더 신중하게 처리되어야 함
•
시뮬레이션은 예측보다 위험 부담이 적음 → 실제 자원의 투입이 필요 없기 때문에 보다 탐구적인 자세로 설계 가능
(but, 시뮬레이션도 구축 방법을 정당화해야 함)
4.2 코드로 보는 시뮬레이션
a.
이메일 열람 행동과 기부의 상관관계의 가설을 검정하기 위한 합성 데이터 시뮬레이션
b.
택시 기사의 교대 시간과 일간 탑승객 빈도에 대한 합성 데이터 시뮬레이션
(파이썬의 제너레이터(generator) 사용)
c.
점진적으로 개별 자기요소(magnetic element)의 위치를 맞춰나가는 자성물질의 물리적 과정 시뮬레이션
(물리 법칙을 활용한 시뮬레이션 구성과 자연적 시간 척도 삽입)
스스로 직접 만들어보기
이메일 열람 행동과 기부의 상관관계의 가설을 검정하기 위한 합성 데이터 시뮬레이션
•
시뮬레이션 프로그래밍을 할 때는 시스템에 적용되는 논리적인 규칙을 명심해야 함
<회원 정의>
•
시뮬레이션 도입 단계
•
회원수, 각 회원의 가입 시점, 각 회원의 상태 정보
•
모든 회원에게 특정 가입 연도 무작위 부여
•
부여된 가입년도에 따라 회원의 상태 정보 결정
# 회원 정의
years = ['2014', '2015', '2016', '2017', '2018']
memberStatus = ['bronze', 'silver', 'gold', 'inactive']
# 발생 확률(p)을 조정해 데이터 생성
memberYears = np.random.choice(years, 1000,
p = [0.1, 0.1, 0.15, 0.30, 0.35])
memberStats = np.random.choice(memberStatus, 1000,
p = [0.5, 0.3, 0.1, 0.1])
yearJoined = pd.DataFrame({'yearJoined': memberYears,
'memberStats': memberStats})
Python
복사
<이메일 열람 테이블 생성>
•
회원의 주간 이메일 열람 시점
•
한 주에 이메일 세 통을 보내는 기관의 행동을 정의한 후 이메일에 관한 회원들의 행동 패턴
NUM_EMAILS_SENT_WEEKLY = 3
# 이메일을 한 번도 열람하지 않은 회원
def never_opens(period_rng):
return []
# 매주 같은 개수의 이메일을 열람한 회원
def constant_open_rate(period_rng):
n, p = NUM_EMAILS_SENT_WEEKLY, np.random.uniform(0, 1)
num_opened = np.random.binomial(n, p, len(period_rng)) # 이항분포에서 난수 생성
return num_opened
# 매주 열람한 이메일의 개수가 늘어나는 회원
def increasing_open_rate(period_rng):
return open_rate_with_factor_change(period_rng, np.random.uniform(1.01, 1.30))
# 매주 열람한 이메일의 개수가 줄어드는 회원
def decreasing_open_rate(period_rng):
return open_rate_with_factor_change(period_rng, np.random.uniform(0.5, 0.99))
def en_rate_with_factor_change(period_rng, fac):
if len(period_rng) < 1 :
return []
times = np.random.randint(0, len(period_rng),
int(0.1 * len(period_rng)))
num_opened = np.zeros(len(period_rng))
for prd in range(0, len(period_rng), 2):
try:
n, p = NUM_EMAILS_SENT_WEEKLY, np.random.uniform(0, 1)
num_opened[prd:(prd + 2)] = np.random.binomial(n, p, 2)
p = max(min(1, p * fac), 0)
except:
num_opened[prd] = np.random.binomial(n, p, 1)
for t in range(len(times)):
num_opened[times[t]] = 0
return num_opened
Python
복사
•
회원의 행동
◦
이메일을 한 번도 열람하지 않은 회원: never_opens()
◦
매주 같은 양의 이메일을 열람한 회원: constant_open_rate()
◦
매주 열람한 이메일의 양이 줄어드는 회원: decreasing_open_rate()
◦
매주 열람한 이메일의 양이 늘어나는 회원: increasing_open_rate()
•
참여율
◦
시간에 따라 참여율이 증가하는 회원: increasing_open_rate()
◦
시간에 따라 참여율이 감소하는 회원: decreasing_open_rate()
⇒ 데이터에 영향을 주는 불확실한 과정(unobservable process)에 대해 전문가들이 경험적 또는 완전히 새롭게 세운 가설에 따라 더 디테일하게 만들 수 있음
<기부 행동 모델링>
•
회원의 행동을 정의하는 가설을 고려한 모델을 만들고 그 가설에 기반한 시뮬레이션이 실제 데이터와 맞아 떨어지는지 검증(너무 단순할 경우 통찰을 얻기 어려움)
•
이메일 열람 횟수와 기부 행동 연결 (느슨한 연결 → 연결은 되지만 정확히 결정짓지는 않도록)
# 기부 행동
def produce_donations(period_rng, member_behavior, num_emails,
use_id, member_join_year):
donation_amounts = np.array([0, 25, 50, 75, 100, 250, 500, 1000, 1500, 2000])
member_has = np.random.choice(donation_amounts)
email_fraction = num_emails / (NUM_EMAILS_SENT_WEEKLY * len(period_rng))
member_gives = member_has * email_fraction # 회원이 기부하는 금액
member_gives_idx = np.where(member_gives >= donation_amounts)[0][-1]
member_gives_idx = max(min(member_gives_idx,
len(donation_amounts) - 2),
1)
num_times_gave = np.random.poisson(2) * (2018 - member_join_year) # 회원이 기부한 횟수
times = np.random.randint(0, len(period_rng), num_times_gave)
dons = pd.DataFrame({'member' : [],
'amount' : [],
'timestamp': []})
for n in range(num_times_gave):
donation = donation_amounts[member_gives_idx + np.random.binomial(1, .3)]
ts = str(period_rng[times[n]].start_time + random_weekly_time_delta())
dons = dons.append(pd.DataFrame(
{'member' :[use_id],
'amount' :[donation],
'timestamp': [ts]}))
if dons.shape[0] > 0:
dons = dons[dons.amount != 0]
# 기부액이 0인 경우에는 보고하지 않음
return dons
Python
복사
<실제와 유사한 행동 반영>
•
회원 자격의 기간에 따라서 기부의 전체 횟수 설정
•
행동 가설: 안정적인 재산이 기부와 밀접한 관련이 있다 → 회원별 재정 상태 고려
•
회원의 행동은 특정 타임스탬프와 연관 → 기부를 한 시점(시간대) 시뮬레이션
# 특정 주 내의 시간을 무작위 선택하는 함수
def random_weekly_time_delta():
days_of_week = [d for d in range(7)]
hours_of_day = [h for h in range(11, 23)] # 시간대 제한
minute_of_hour = [m for m in range(60)]
second_of_minute = [s for s in range(60)]
return pd.Timedelta(str(np.random.choice(days_of_week)) + " days" ) + pd.Timedelta(str(np.random.choice(hours_of_day)) + " hours" ) + pd.Timedelta(str(np.random.choice(minute_of_hour)) + " minutes") + pd.Timedelta(str(np.random.choice(second_of_minute)) + " seconds")
Python
복사
•
(hours_of_day = [h for h in range(11, 23)])
◦
시간(timestamp) 제한 : am 11:00 - pm 11: 00 (이외 시간 허용 X)
▪
기부 발생 시간은 늦은 아침부터 늦은 저녁 사이라는 내용을 가정
▪
회원의 행동 방식에 대한 근본적 모델 구축을 위해 시간대를 재구성하기도 함
→ 회원들 간의 통일된 행동 방식 기대
<전체 코드>
behaviors = [never_opens,
constant_open_rate,
increasing_open_rate,
decreasing_open_rate]
member_behaviors = np.random.choice(behaviors, 1000, [0.2, 0.5, 0.1, 0.2])
rng = pd.period_range('2015-02-14', '2018-06-01', freq = 'W')
emails = pd.DataFrame({'member' : [],
'week' : [],
'emailsOpened': []})
donations = pd.DataFrame({'member' : [],
'amount' : [],
'tunestamp': []})
for idx in range(yearJoined.shape[0]):
# 회원이 가입한 시기 무작위 생성
join_date = pd.Timestamp(yearJoined.iloc[idx].yearJoined) + pd.Timedelta(str(np.random.randint(0, 365)) + ' days')
join_date = min(join_date, pd.Timestamp('2018-06-01')).to_period(freq='W')
# 가입 전 어떤 행동에 대한 타임스탬프도 가지면 안됨
member_rng = rng[rng > join_date]
if len(member_rng) < 1:
continue
info = member_behaviors[idx](member_rng)
if len(info) == len(member_rng):
emails = emails.append(pd.DataFrame(
{'member': [idx] * len(info),
'week': [str(r.start_time) for r in member_rng],
'emailsOpened': info}))
donations = donations.append(
produce_donations(member_rng, member_behaviors[idx],
sum(info), idx, join_date.year))
Python
복사
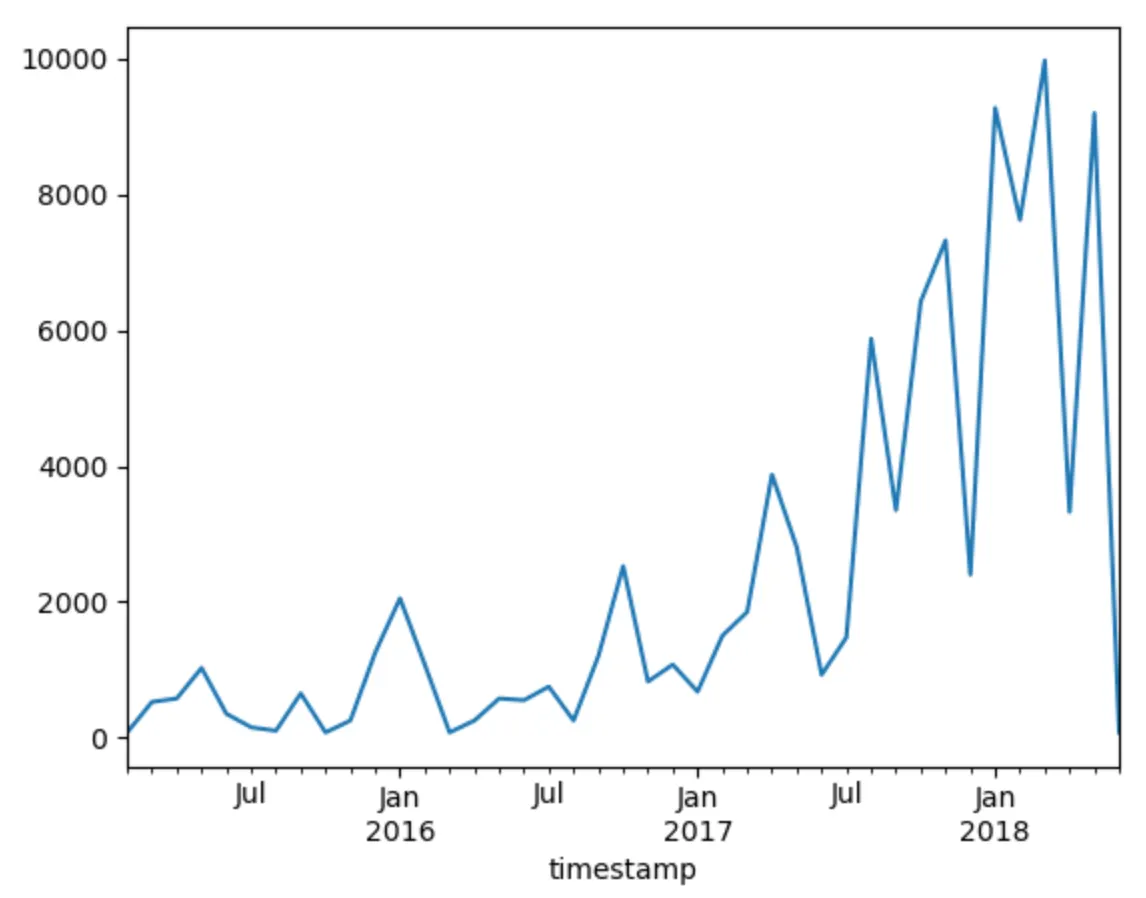
<월별 기부의 총합에 대한 도표>
donations.set_index(pd.to_datetime(donations.timestamp), inplace = True)
donations.sort_index(inplace = True)
donations.groupby(pd.Grouper(freq='M')).amount.sum().plot()
Python
복사
•
시간의 흐름(2015→2018)에 따라 기부 및 이메일 열람 횟수 증가
◦
매년 신규 회원의 유입으로 누적 회원 수가 증가했기 때문에 열람된 이메일의 수 증가
•
모델에 한 회원이 가입한 시점으로부터 그 회원의 자격이 무기한으로 유지된다는 가정이 내재됨(회원 해지에 대한 조항이 없으므로)
•
시간의 흐름에 따라 점점 더 적은 수의 이메일을 열람하도록 설계됐지만, 지속적인 기부의 가능성은 열려있음
◦
무기한적인 회원 자격과 이에 따른 기부 행동 방식에 대한 가정으로 인한 기부 행동 방식은 비현실적
⇒ 오류 방지를 위해 표준적인 유효성 및 유효성에 대한 외부 측정 기준을 시뮬레이션 수행 전에 정립하는 것이 좋음
•
비논리적으로 발생하는 사건, 예외적인 상황 등
→ 파이썬의 제너레이터를 사용(보다 나은 방식으로 논리적이고 일관성 있는 세계 구성)
스스로 실행하는 시뮬레이션 세계 구축
•
시스템이 흘러가는 과정을 관찰해보고 싶은 경우 시뮬레이션을 구축함.
→ 시간에 따른 종합적인 측정 기준으로 개별 에이전트의 기여 방식을 확인해야 함.
•
Python의 “Generator” 기능이 매우 적합함.
•
Generator? iterator를 생성해주는 함수
◦
iterable한 순서가 지정됨(모든 generator는 iterator에 해당함.)
◦
함수의 내부 로컬 변수를 통해 내부상태가 유지됨.
◦
무한한 순서가 있는 객체를 모델링할 수 있다. (명확한 끝이 없는 데이터 스트림)
◦
자연스러운 스트림 처리를 파이프라인으로 구성할 수 있다.
제네레이터는 독립적이거나 의존적인 일련의 Actor를 생성하고, 시간을 돌려가며 각 Actor가 하는 일을 관찰할 수 있게 해줌.
•
택시 시뮬레이션 - 서로 다른 시간에 교대근무가 예정된 택시 무리의 전체 행동 방식 시뮬레이터(여러 개별 택시를 생성하여 행동을 보고받는 방식)
1.
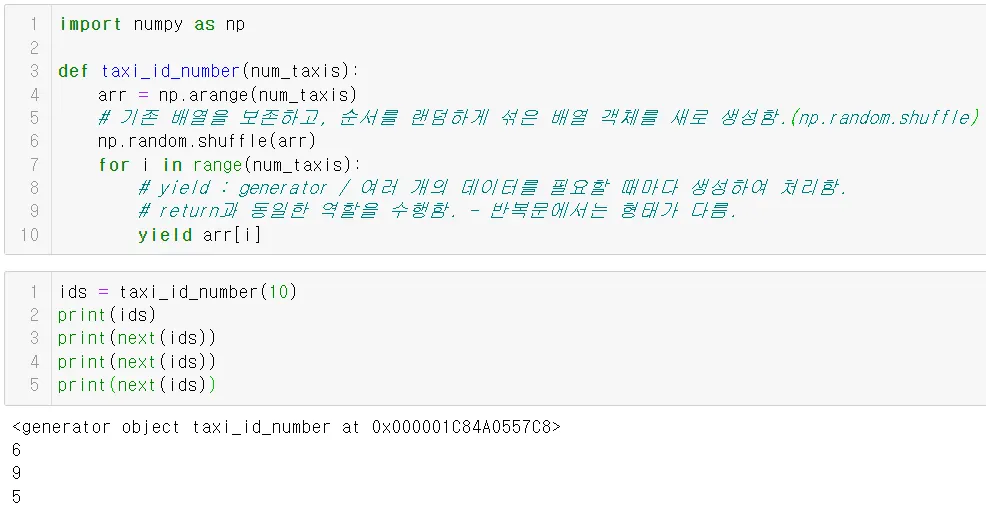
택시의 식별 번호 생성 함수
•
yield 키워드를 통해 generator를 생성하며, yield가 호출되면 암시적으로 return이 호출되고, 한번 더 실행되면 ‘yield’ 다음 코드가 실행됨.
•
next(): 배열 내에 포함된 데이터를 하나씩 불러옴.
2.
밤이나 새벽보다 낮에 더 많은 택시를 할당하는 특정 시간 교대근무 확률 부여
•
하루의 서로 다른 세 개의 교대 시간대 표현 및 각 시간대에 택시가 할당될 서로 다른 확률 부여
•
시간 : 0, 8, 16, 빈도 : 8, 30, 15
3.
개별 택시의 파라미터를 설정하고, 시간표 생성
•
두 개의 제너레이터를 통해 각 택시의 ID 번호, 교대 시작 시간, 해당 횟수에 따른 평균 운행 횟수 결정
◦
각 택시는 특정 시간대에 근무를 시작하고, 해당 시간대에 예상되는 평균 운행 횟수를 지니고 있음.
◦
정규 분포를 사용하여 실제 운행 횟수를 결정하고, 각 운행 사이의 시간을 계산함.
택시의 활동 : 운행 시작 → 손님 탑승 → 손님 하차
Poisson Distributions
→ 개별 택시 객체는 정해진 역할을 스스로 수행하며, next() 호출로 taxi_process 제너레이터에 접근하는 클라이언트에게 결과를 보여줌.
푸아송 분포를 통해 deltaT를 추출 → 다음 이벤트 발생 시간을 의미함.(time 변수 갱신)
4.
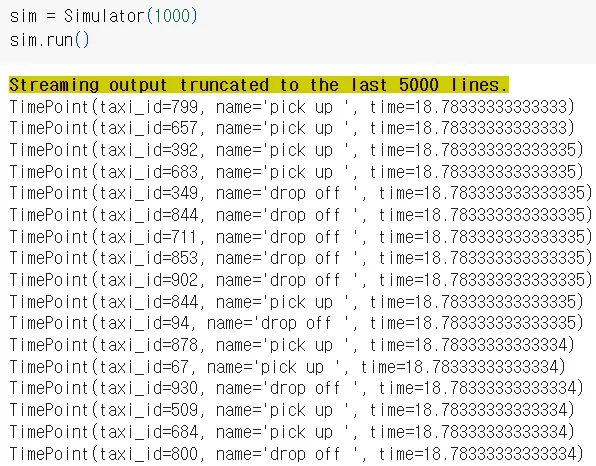
택시 제너레이터에 의해 생성되는 TimePoint 객체 형태
•
시간과 이벤트를 나타내는 클래스 생성
◦
taxi_id : 택시의 고유 식별자
◦
name : 이벤트의 이름(’start shift’, ‘pick up’, ‘drop off’, ‘end shift’, … etc)
◦
time : 이벤트 발생 시간
dataclass(Decorator)
5.
시뮬레이션을 위한 클래스 정의
•
택시 시뮬레이션을 관리하며, 앞서 정의한 택시 제너레이터들을 조합함.
◦
택시 개수에 따른 제너레이터 생성
◦
택시 제너레이터에 반복적으로 접근하여 반환한 TimePoint가 유효하다면, 해당 TimePoint를 우선순위 큐에 input함.
◦
시작 시간을 비교하여 객체의 우선순위를 지정함.
◦
우선순위 큐에 쌓인 TimePoint가 시간의 순서대로 Output 되도록 준비함.
•
‘_prepare_run’ : 각 택시의 작업을 생성하고 시간 순서대로 정렬하는 역할로, 시뮬레이션을 준비함.
•
‘run()’: 시간이 24시간을 초과하지 않는 한 계속하여 택시 이벤트를 처리하고 출력함.
•
초기화 시 택시의 수를 인수로 입력받음.
•
라이브 스트림에서 발생하는 사건을 기록하는 것과 같음.
→ 택시 운영을 모의로 시뮬레이션하여 실제 운영 상황을 예측하고 택시 서비스를 최적화하는 데 도움을 줄 수 있음.
•
시뮬레이션을 통한 근본적인 역동성에 다양한 예측 모델을 접목하여 여러 가지 가치를 판단할 수 있음.
•
실제 데이터를 손에 넣기 전까지, 합성된 데이터를 활용하여 예상되는 데이터 파이프라인을 구축해볼 수 있음.
물리적인 시물레이션
•
물리적인 법칙을 완전히 꿰고 있는 상황
금융계 퀀트 연구원 ->시장의 물리적인 규칙
심리학자->정신 물리학적 규칙
생물학자 자극에 대한 시스템 반응 규칙
•
자석에 대한 모델링-> Ising model로부터 시작
100도 에서 물의 상태 변화, 자석의 퀴리 온도 등에서의 상태 변화와 같은 급격한 변화를 설명 하기 위한 1차원 모델을 제시. Wilhelm Lenz와 그 제자 Ising
상전이는 2차원 이상에서만 존재
자성체를 초기화. > 개별 자성 요소가 무작위적인 방향을 가리키도록 해줌 > 물리법칙 코드 작성 > 시스템
•
몬테카를로
몬테카를로 방법은, 수식만으로 계산하기 어려운 문제가 있을 때 데이터의 무작위 샘플을 얻은 뒤 그 샘플을 이용해서 답을 구하는 방법
예) 반지름이 1인 원의 넓이를 구하는 문제. (직관적인 답)
1. 2차원 좌표계 위에 원점을 중심으로 가로와 세로 길이가 2인, 넓이 4짜리 정사각형을 그린다.
2. 이 사각형 안에 무작위로 점을 찍는다.
3. 그 점들 중에서 원점으로부터의 거리가 1이하인 점(이게 바로 원의 정의다)의 비율을 계산한다.
4. 이 비율을 사각형의 넓이 4에 곱하면, 우리가 원하는 반지름 1짜리 원의 넓이 추정값이 된다.
점을 찍는 시도가 많아질수록 추정치는 실제 값에 가까워짐.
•
마코프 체인
체인은 상태 값의 시퀀스. 각각의 상태는 서로 독립이 아니라 이전의 상태에 영향을 받음. 오늘의 날씨는 어제, 그제의 날씨와 무관하지 않다.
하루 전에 화창했다면, 하루 전 비가 왔을 때에 비해서, 오늘 맑을 확률이 더 높을 것이다.
마코프 체인에서 각 상태는 바로 이전의 사태에 ”만” 영향을 받는다고 가정.
즉, 내일의 날씨는 오늘의 날씨와만 관련이 있고, 어제 이전의 날씨와는 독립이라고 봄.
마코프 체인의 흥미로운 특성 한 가지는, 몇 가지 추가 조건이 만족한다면, k가 충분히 커지면 Xk의 분포는 특정한 값으로 수렴한다.
우리의 날씨 마코프 체인에는 총 4가지의 상태 전이확률(Transition Probabilities)이 있다. P(맑음 | 맑음), P(비 | 맑음), P(맑음 | 비), P(비 | 비). 그리고 P(맑음 | 맑음) + P(비 | 맑음) = P(맑음 | 비) + P(비 | 비) = 1이라고 하자. 오늘 날씨가 맑다면, 이 전이확률을 이용해서 내일 맑을 확률과 비가 올 확률을 계산할 수 있다. 그리고 다시 그 값을 이용해서 모레의 날씨의 확률분포를 계산할 수 있다. 이 과정을 계속 반복하다 보면 어느 순간부터 그날의 날씨 확률분포가 그 전날과 같아지는 때가 온다.이렇게 평형 상태에 도달한 날씨의 확률분포를 Stationary Distribution이라고 부른다.
이 Stationary Distribution은 초기값에 연연하지 않는다는 점이다. 위에서는 시뮬레이션을 시작할 때 오늘이 맑다고 가정했지만, 비가 온다고 가정했더라도 최종적으로 수렴하는 확률분포는 동일하다.
•
마코프 체인 몬테카를로
MCMC 알고리즘은 우리가 샘플을 얻으려고 하는 목표 분포를 Stationary Distribution으로 가지는 마코프 체인을 만듬. 이 체인의 시뮬레이션을 가동하고, 초기값에 영향을 받는 burn-in period를 지나고 나면, 목표분포를 따르는 샘플이 만들어짐. 그런 마코프 체인을 만들 수 있는 방법
Metropolis와 이를 일반화한 Metropolis-Hastings, 그리고 깁스 샘플링(Gibbs Sampling)이 있음.
자성 요소 일 방향 정돈
•
규칙의 적용
마르코프 과정에서 미래의 상태로 천이할 확률은 현재의 상태에만 의존.
볼츠만 에너지 분포 Ty / Tjt = e~b(Ej'£i)조건 도입
•
시뮬레이션
격자 lattice의 각 지점에 대한 시작 상태를 무작위로 선택합니다.
각 시간 단계마다 하나의 격자 지점을 선택,그 지점의 방향을 뒤집음.
에너지의 변화를 계산
에너지의 변화가 음성이라면 더 낮은 에너지 상태로 천이 or 음성이 아니라면 에너지 변화의 수용확률
e(-에너지 변화) (acceptance probability)로 상태 천이
•
시스템의 환경 설정
python
» > m 환 경 설 정
»> ## 물리적 배치
»> N = 5 # 격자 너비
»> M = 5 # 격자 높이
»> ## 온도 설정
»> temperature = 0.5
»> BETA = 1 / temperature
•
시작 블록 무작위 초기화 하는 유틸리티 함수 정의
»> def initRandState(N, M):
»> block = np.random.choice([-l_, 1]_, size = (N, M))
»> return block
•
인접 상태에 비례하여 중앙 정렬 상태의 에너지를 계산
python
»> def costForCenterState(state, I, j, n, m)
»> centerS = state[I, j]
»> neighbors=[((i + 1) % n, j),((i - 1) % n, j),
(i, (j + 1) % m), (i,(j - 1) % m)]
»> ##주기적 경계 조건의 상정을 위한 % n 부분에 주목
»> interactionE = [state[x, y] * centers for (x, y) in neighbors]
»>return np.sum(interactionE)
•
주어진 상태에서 전체 블록의 자화 (magnetization)를 결정
python
»> def magnetizationForState(state):
»> return np.sum(state)
•
MCMC의 한 단계에 대한 코드
python
»> def mcmcAdjust(state):
»> n = state.shape[0]
»> m = state.shape[1]
»> x, y = np.random.randint(0, n), np.random.randint(0, m)
»> centerS = state[x, y]
»> cost = costForCenterState(state, x, y, n, m)
»> if cost < 0:
»> centers *= -1
»> elif np.random.random() < np.exp(-cost * BETA):
»> centers *= -1
»> state[x, y] = centers
»> return state
•
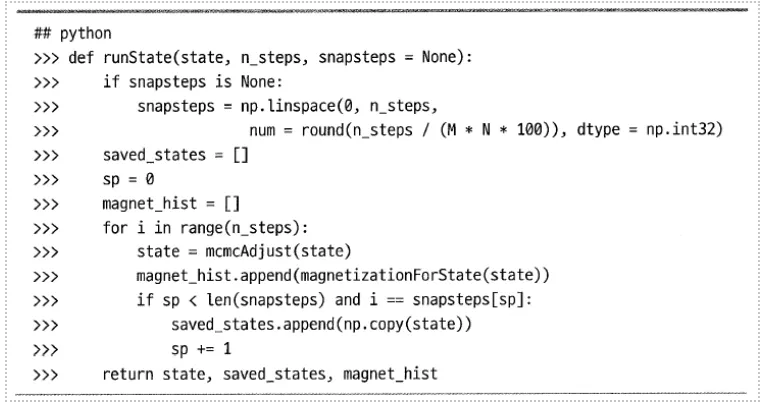
mcmcAdjust를 반복적으로 호출하면서,조정되는 상태를 기록
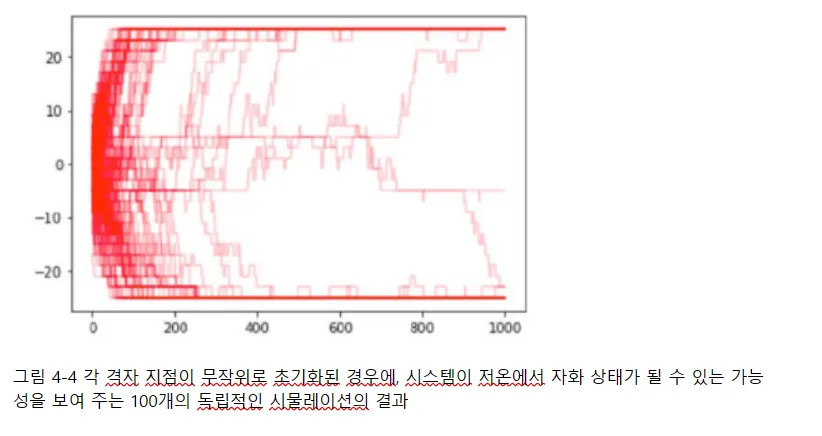
⦁ 시뮬레이션 실행
시물레이션을 여러 번 독립적으로 실행. 시간에 따른 자화의 도표를 그림
•
택시 시뮬레이션과의 유사점
시물레이션된 데이터를 작업 공정의 설정을 위한 자극제로 사용.
이렇게 합성된 데이터에 머신러닝 기법을 우선 적용하여, 물리적인 데이터에서 머신러닝
기법의 유효성을 확인. 실세계 데이터를 다룰 때는 특정 모델을 적용하기까지 데이터를 정리 등에서 여러 난관이 발생. 따라서 모델의 유효성을 빨리 확인할 필요가 있다면 합성된 데이터를 활용.
시스템의 더 나은 물리적 직관을 얻기 위해서 동영상이나 이미지 형식으로 중요한 측정기준을 관찰
4.3 시뮬레이션에 대한 마지막 조언
통계적인 시물레이션
•
시뮬레이션된 시계열 데이터를 얻는 가장 전통적인 방법
시스템의 근간이 되는 확률적인 역동성을 이미 알고 있을 때, 몇 가지 모르는 파라미터를 추정하거나 서로 다른 가정이 파라미터 추정 과정에 주는 영향을 알아보고자 한다면 유용
•
시뮬레이션 정확도에 대한 불확실성을 정의하는 분명한 양적 측정지표가 필요한 경우에도 꽤 가치 있다.
•
딥러닝 시물레이션
•
시계열 데이터에서 매우 복잡할 수 있는 비선형적 역동성을 잡아낼 수 있다. 하지만 시스템 역동성의 근본 원리를 전혀 이해하지 못하게 될 수 있다.