Search

Isolation Forest

1. 이론적 배경

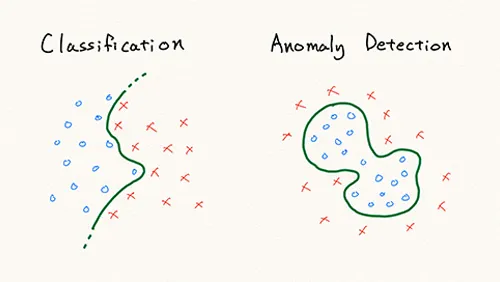
1.1 이상치 탐지(Anomaly Detection) 문제점

문제점:
•
이상치 데이터들을 하나의 정형화된 패턴으로 분류하기 어려울 수 있다.
•
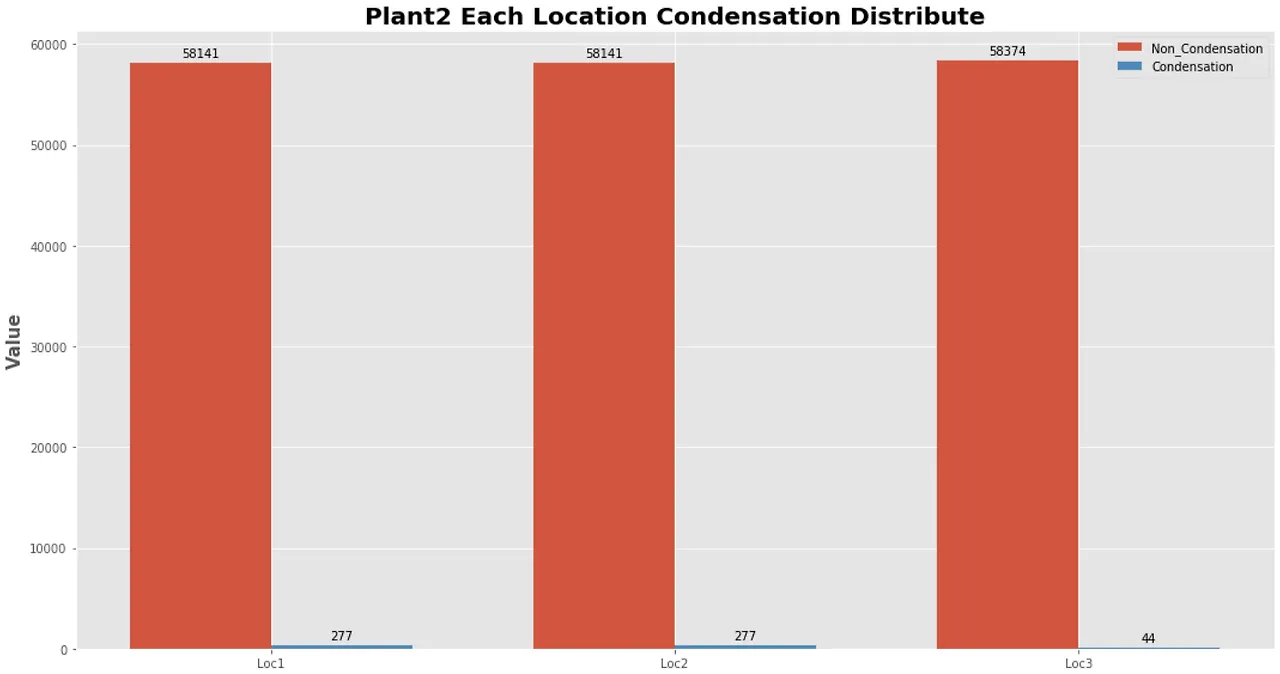
데이터 간의 불균형이 매우 심하면, 모델이 정상 데이터에 편향될 가능성이 높다.
ex) 정상 데이터 : 99.98%, 이상치 데이터 : 0.02%10000개의 데이터 셋에서 9998개가 정상 데이터이고,
만약에 10,000개의 데이터에서 1과 0의 비율이 9998 : 2 비율을 갖고 있다면,
모든 값을 1로 예측해도 정확도가 99.98%가 나오게 된다.
출처 : shinminyong 티스토리
•
distance나 density 기반 알고리즘은 계산 비용(computational cost)이 높다.
따라서, large dataset (high-dimensional 데이터)에 적용하기 어렵다.
대부분의 비지도 학습을 이용한 anomaly detection은 training 데이터를 이용해 데이터 포인터 간의 distance나 density를 계산하여 정상 범주를 정의합니다.
그리고 test 데이터에서 distance나 density를 계산하여 정상 범주에 들어가지 않으면 이상치로 판단합니다.
출처 : MakinaRocks

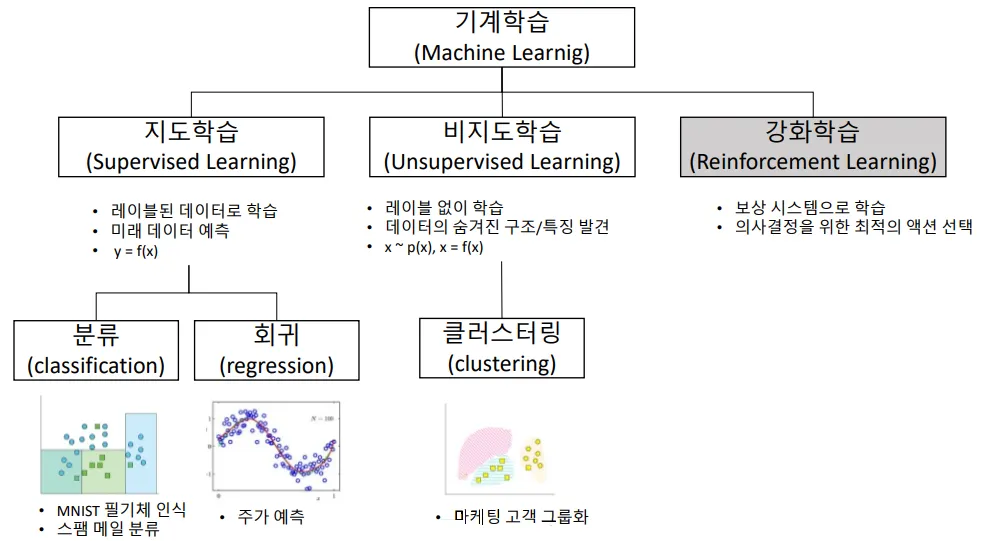
1.2 Decision Tree

정의 :
•
분류와 회귀 문제에 널리 사용하는 모델
출처 : ittrue 티스토리
•
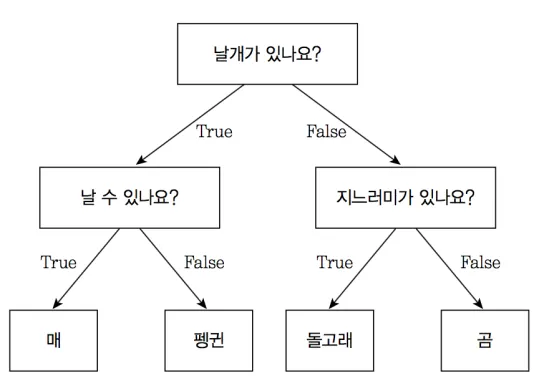
특정 질문(기준)에 따라 데이터를 구분하는 모델
출처 : 텐서 플로우 블로그
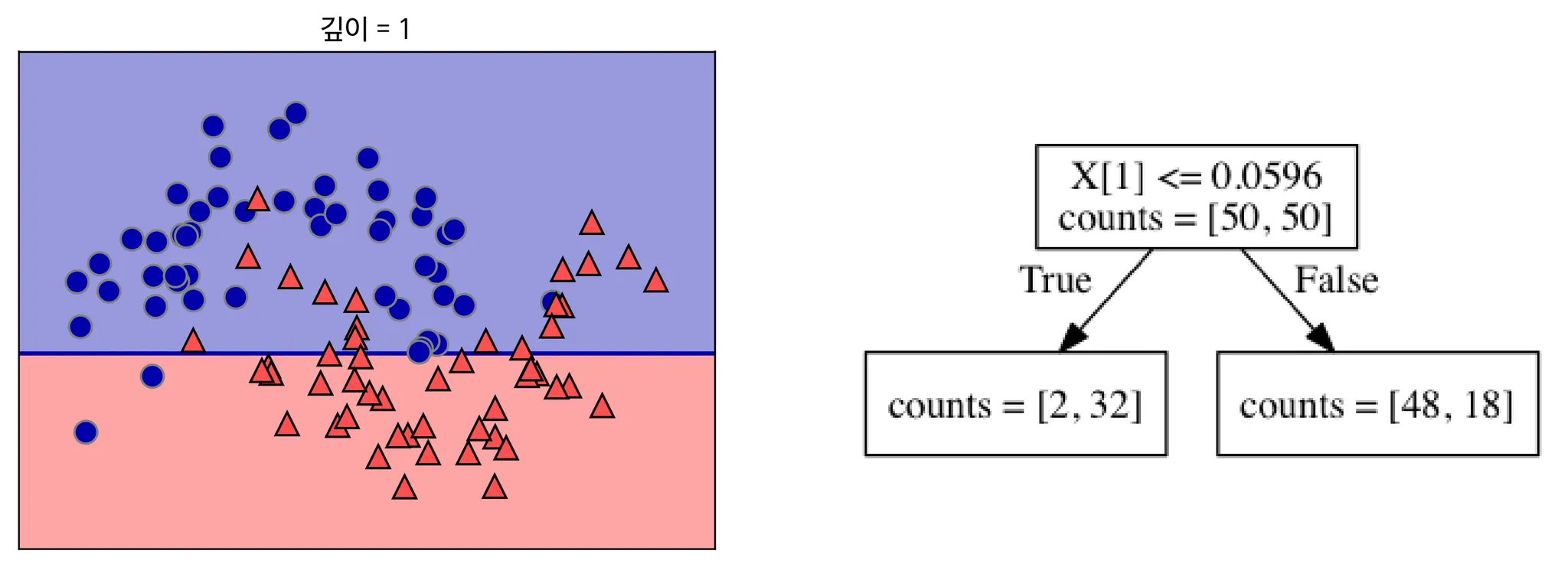
출처 : 텐서 플로우 블로그
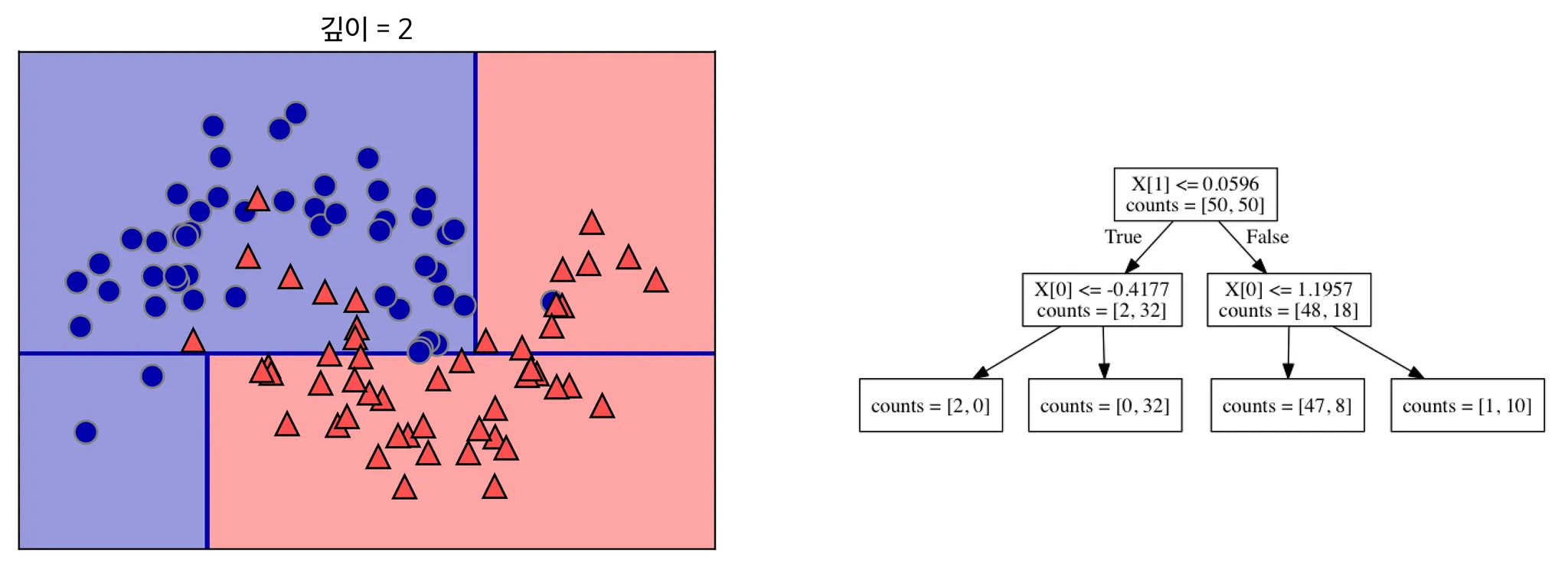
출처 : 텐서 플로우 블로그
Pruning (가지치기):
•
오버피팅(트리에 가지가 너무 많은 경우)을 막기 위한 전략
a.
최대 깊이(max_depth)를 제한
ex) max_depth = 4로 설정하면, 깊이가 4보다 크게 분기를 하지 않는다.
b.
터미널 노드의 최대 개수를 제한
c.
한 노드가 분할하기 위한 최소 데이터 수 제한
ex) min_sample_split = 10으로 설정하면, 한 노드에 10개의 데이터가 존재하면 더 이상 분기를 하지 않는다.
출처 : datanetworkanalysis.github.io (isolation)

1.3 Bagging

앙상블(Ensemble) 정의 :
•
여러 개의 Decision Tree를 결합하여 하나의 Decision Tree보다 더 좋은 성능을 내는 머신러닝 기법
•
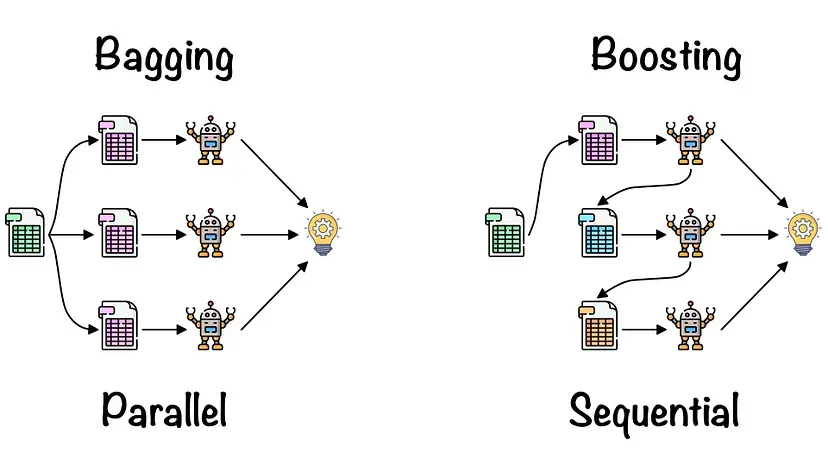
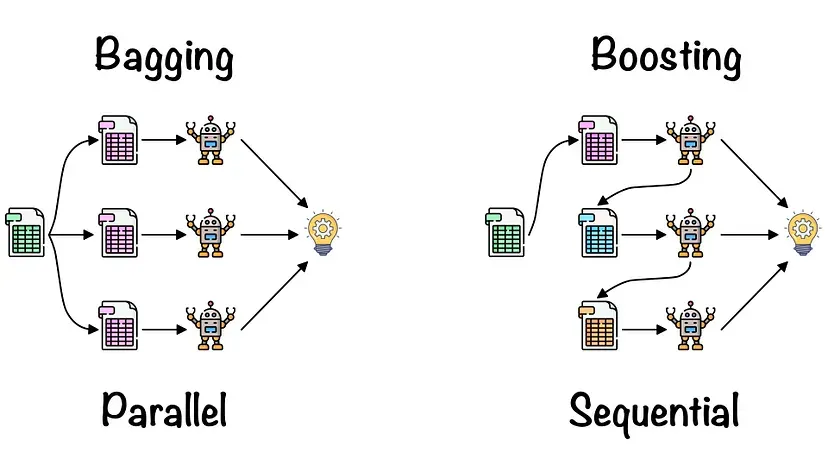
앙상블 학습법에는 Bagging과 Boosting이 있다.
출처 : Roshmita Dey’s Meduium
부트스트랩(Bootstrap) 정의 :
Bootstrap 어원
•
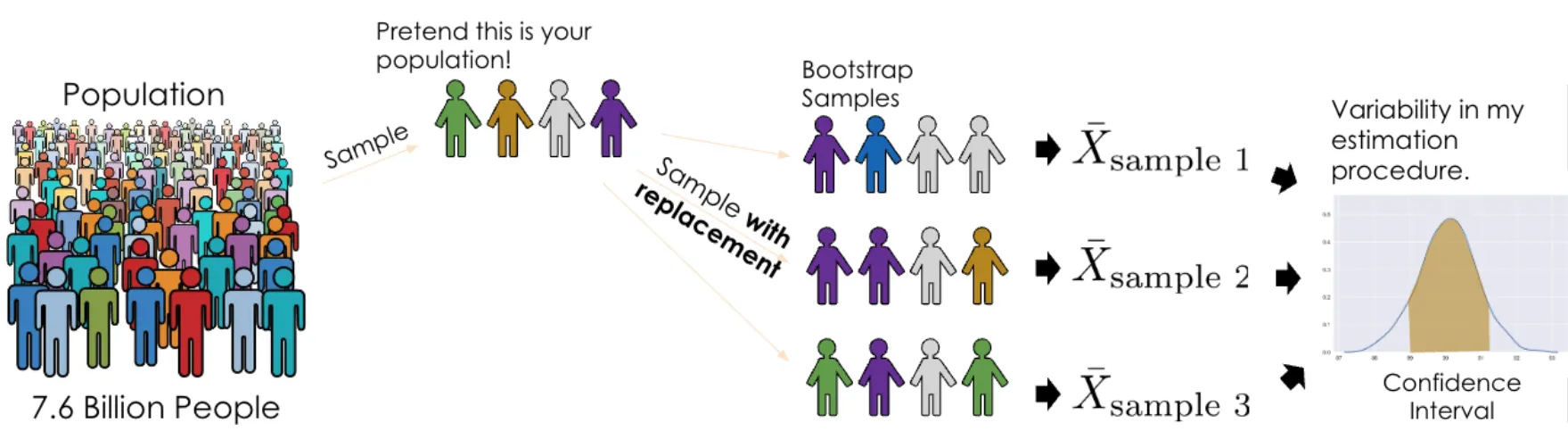
표본을 모집단으로 여기고 표본을 복원추출 방식으로 계속 반복해서 표본을 재추출하는 방법
•
중심극한정리 이론을 위해 표본을 무수히 추출해야 하나, 현실적으로 어려울 때 사용하는 방법
Bootstrap 예시 (출처: ds100.org)
•
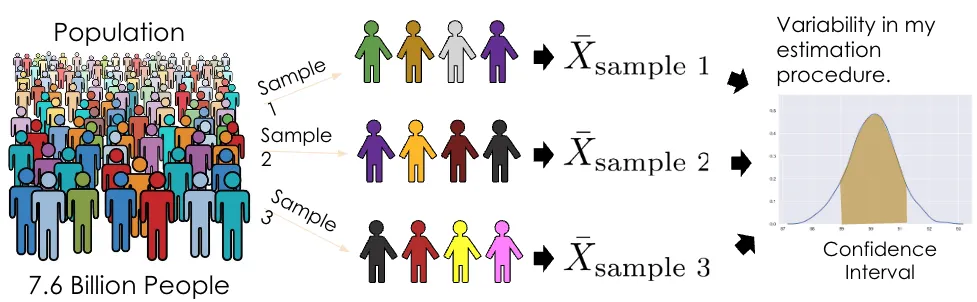
cf) 중심극한정리(Central Limit Theorem)와 비교해보기
중심극한정리 예시(출처 : ds100.org)
중심극한정리는 동일한 모집단으로부터 무작위로 n개의 샘플을 추출해 평균을 계산했다고 해보자.
n→∞(n이 무한대로 갈 경우) 라면, 샘플의 평균의 분포가 정규분포에 근사한다는 정리이다.
그러나, 모집단에 대한 정보가 없거나 단일 샘플만 있는 상황이라면 중심극한정리를 사용할 수 없다.
이러한 상황에서 Bootstrap은 하나의 샘플을 모집단으로 간주하고, 해당 샘플에서 n개의 샘플을 재추출하면(n→∞), 이들의 평균도 정규분포에 근사한다는 정리이다. 단, 하나의 샘플이 모집단을 잘 대표하고 있다는 전제가 필요합니다.
배깅(Bagging) Bootstrap Aggregation) :
•
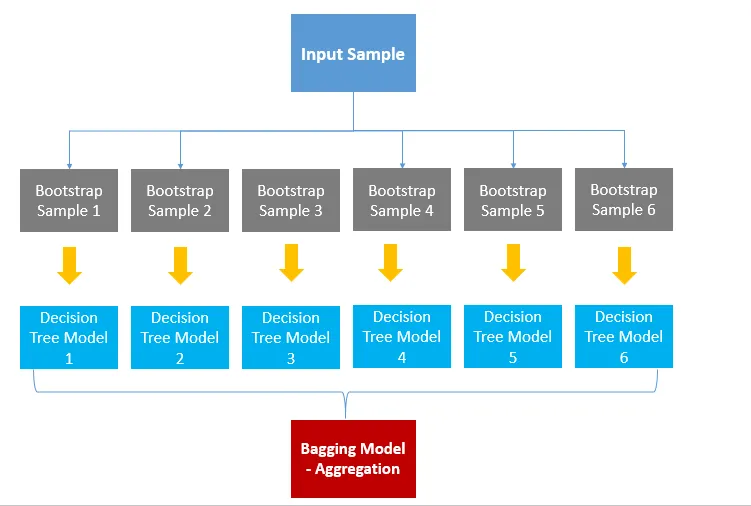
샘플을 Bootstrap(복원 랜덤 샘플링)하여 각 모델을 부트스트랩한 데이터로 학습시키고, 집계하는 방법
출처 : Roshmita Dey’s Meduium
여기서 핵심은 Input이 Sample이라는 점과 병렬로 학습한다는 점. (출처 : swallow.github.io)
•
cf) Boosting과 비교해보기
출처: Medium (Boosting and Bagging explained with examples)
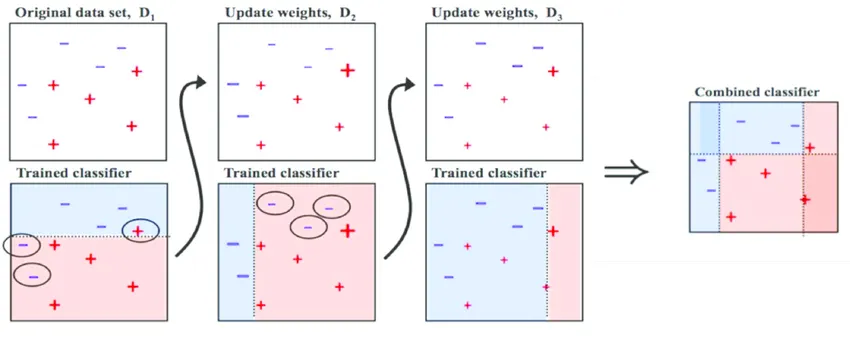
Bagging은 병렬로 학습하는 모델들이 서로 독립적이지만,
Boosting은 순차적으로 학습하므로, 처음 모델이 예측한 결과에 따라 데이터에 가중치가 부여되어 다음 모델에 영향을 준다. Boosting은 Bagging에 비해 error가 적지만, 속도가 느리고 오버 피팅이 될 가능성이 있습니다.

1.4 조화 급수(Harmonic Series)와 오일러–마스케로니 상수(Euler–Mascheroni Constant)

이 부분은 수학적인 배경지식이 많이 필요한 부분이므로, 궁금하시거나 수학에 관심이 많으신 분들만 참조 부탁드립니다.
Q: 왜 노드 n개의 Binary Search Tree의 평균 path length는 H(n-1)과 비례하는가?

2. Isolation Forest

가정:
1.
Abnormal data(이상치)는 normal data보다 훨씬 더 적은 개수로 구성되어 있다.
2.
Abnormal data는 normal data와 매우 다른 attrivute-values(속성-값)들을 가지고 있다.
정의 :
•
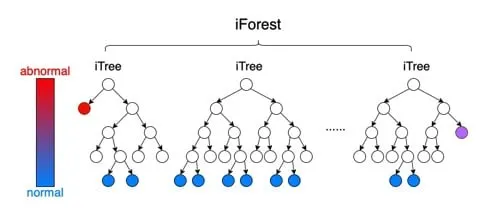
iTree는 각 노드에서 무작위적(random split)으로 속성(attribute)와 값(split value)을 선택하여,
하나의 인스턴스와 나머지로 분할(partition)하는 트리를 의미한다.
•
iTree에서 특정 객체 하나를 고립시켰을 때,
◦
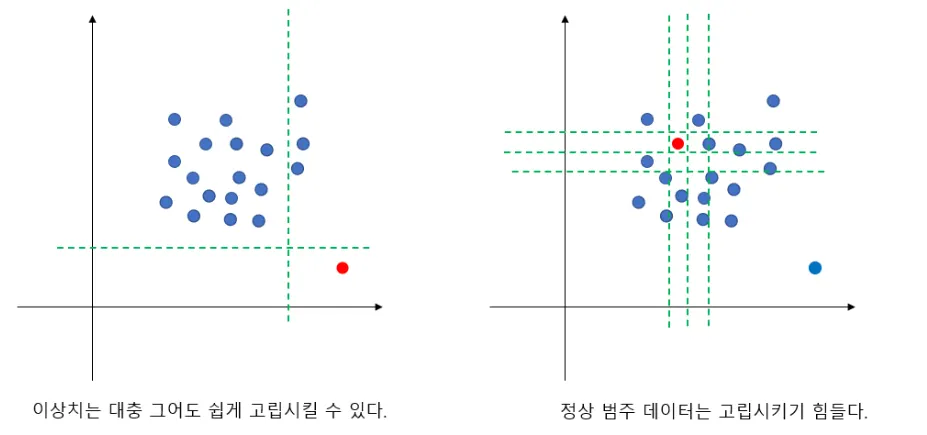
Abnormal data(이상치: anomaly)
▪
고립시키기 쉽다.
▪
적은 split으로 isolation이 가능하다.
◦
normal data
▪
고립시키기 어렵다.
▪
isolation을 시키는데 많은 split이 필요하다.
iTree는 Bootstrapping을 이용해 random하게 split한 결과이므로,
Bootstrap의 개념에 의해 각 트리의 split 횟수(path length)들의 평균을 구해서 위와 같은 결과를 도출한다. (ensemble 개념)
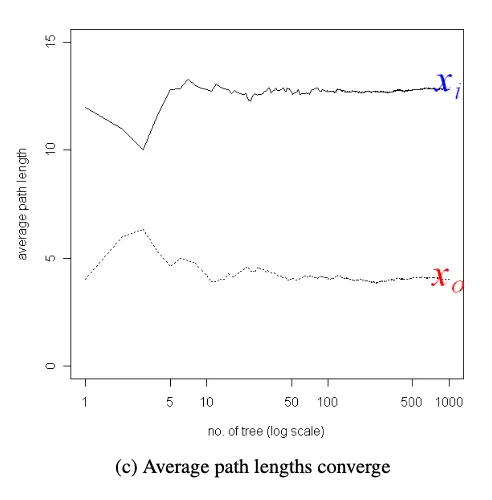
iTree들의 split 횟수를 평균을 구해보니,
abnormal data는 평균 12~13회 정도로 나타내고,
normal data는 4회 정도로 도출된다.
Bootstrap에서 sample로부터 sub-sample들을 n개(n→∞)를 추출하므로,
iTree의 개수를 log scale로 증가시키면서 평균을 구하는 이유를 이해할 수 있을 것이다.
Path length (=h(x)) :
•
the number of edges x traverses an iTree from the root node to the terminal node in which the instace x is located.
⇒ Root node로부터 객체 x가 속해 있는 terminal node까지 거쳐간 edge의 수
•
x가 고립될 때까지 필요한 분할 횟수
anomaly score (Novelty score) (=s(x,n)) :
s(x,n)=2−E(h(x))c(n)s(x,n)=2^{-\frac{E(h(x))}{c(n)}}
E(h(x))→c(n),s→0.5E(h(x))\rightarrow c(n), s\rightarrow 0.5
xx의 평균 경로 길이가 트리의 평균 경로 길이와 비슷한 경우
E(h(x))→0,s→1E(h(x))\rightarrow 0, s\rightarrow 1
xx의 평균 경로 길이가 매우 짧은 경우(= 루트 노드 근처에서 고립된)
E(h(x))→n−1,s→0E(h(x))\rightarrow n-1, s\rightarrow 0
xx의 평균 경로 길이가 긴 경우(= 최대 깊이 근처에서 고립된)
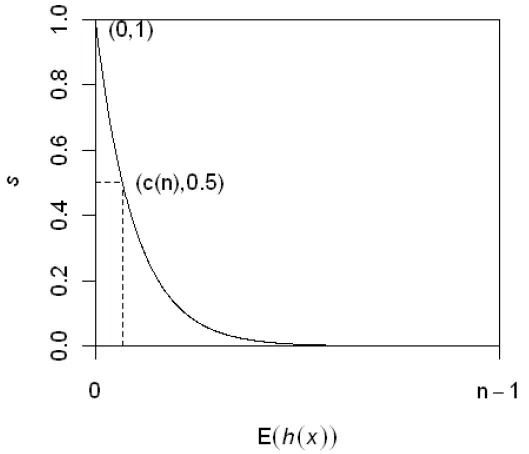
인스턴스 xx의 평균 경로 길이 E(h(x))E(h(x))와 이상 점수 ss와의 관계 (출처 : 안현 교수님 연구노트)
•
E(h(x))
: isolation forest에 존재하는 iTree들의 평균 path length
◦
특정 객체 x를 기준으로 평균 path length를 계산
•
c(n)
n개의 노드로 이루어진 Binary Search Tree에서 root부터 isolation된 객체(external node)까지의 평균 path length
◦
n개의 노드 개수 기준으로 평균 path length를 계산
c(n)=2H(n−1)−(2(n−1)/n)c(n)=2H(n-1)-(2(n-1)/n)
•
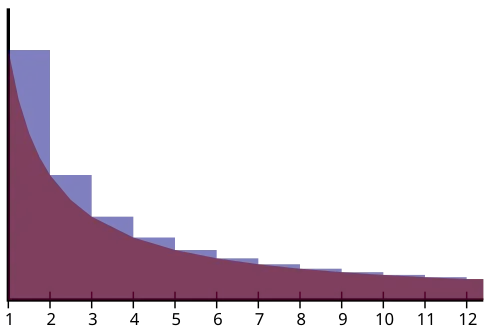
H(n) : 조화수 (Harmonic number)
◦
조화 급수(각 항의 역수가 등차수열을 이루는 급수)의 n항까지의 부분합
H(i)=∑k=1i1k=1+12+13+⋯+1iH(i) = \sum_{k=1}^{i} \frac{1}{k} = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{i}
Hn≈ln⁡(n)+γH_n \approx \ln(n) + \gamma
출처 : wikipedia.org/wiki/오일러-마스케로니_상수

3. 코드 구현

isolation forest.ipynb
6.0KB
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.ensemble import IsolationForest from sklearn.datasets import make_blobs
Python
복사
데이터 생성 :
# 정상 데이터 X, _ = make_blobs(n_samples=300, centers=1, cluster_std=0.60, random_state=42) # 정상 데이터 확인해보기 X[1:10]
Python
복사
array([[-2.06082146, 9.38050829], [-2.87022159, 10.12565304], [-2.44108722, 9.41156453], [-3.99218432, 8.53614897], [-3.13154532, 8.90008292], [-3.00252986, 9.16049846], [-1.8143311 , 9.48928374], [-3.01272814, 8.8287587 ], [-2.33335414, 8.58567528]])
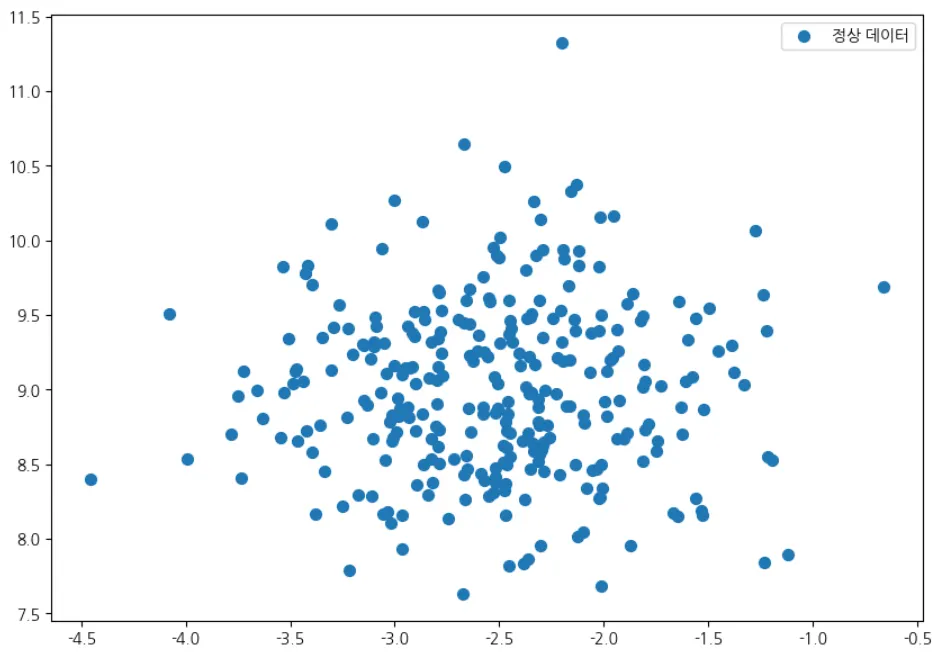
# 정상 데이터 시각화 plt.figure(figsize=(10,7)) plt.scatter(X[:300,0],X[:300,1], label ='정상 데이터', s=50) plt.legend(loc='best') plt.rcParams['font.family'] = 'NanumMyeongjo' plt.show()
Python
복사
#이상치 추가 rng = np.random.RandomState(42) X_outliers = rng.uniform(low=-6, high=6, size=(20,2)) X = np.vstack([X,X_outliers])
Python
복사
데이터 시각화 :
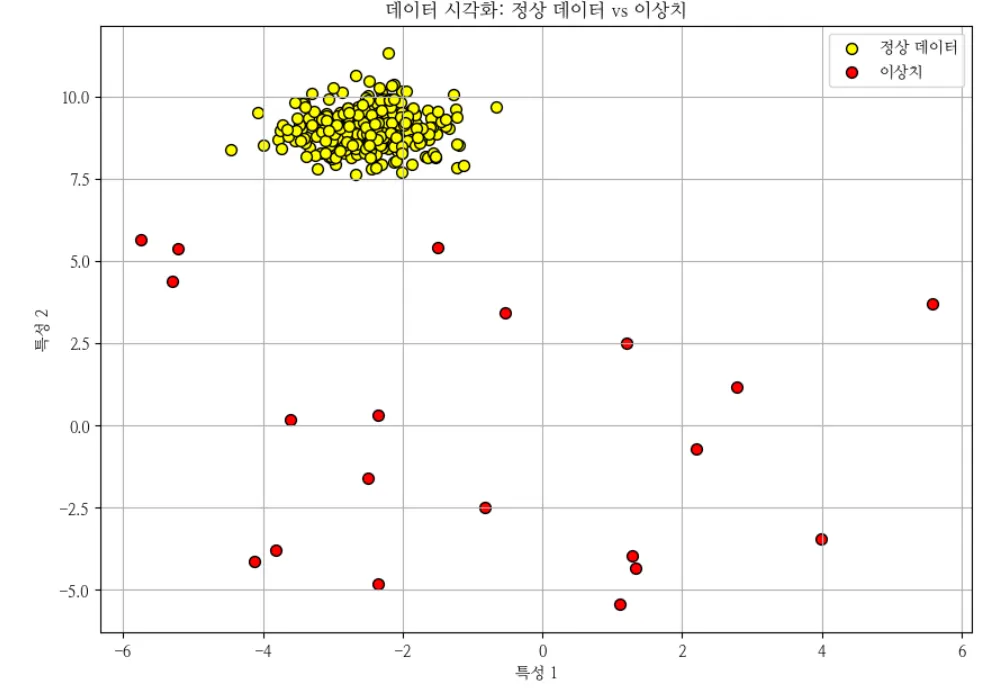
plt.figure(figsize=(10, 7)) plt.scatter(X[:300, 0], X[:300, 1], c='yellow', label='정상 데이터', edgecolor='k', s=50) plt.scatter(X[300:, 0], X[300:, 1], c='red', label='이상치', edgecolor='k', s=50) plt.title('데이터 시각화: 정상 데이터 vs 이상치') plt.xlabel('특성 1') plt.ylabel('특성 2') plt.legend() plt.grid(True) plt.show()
Python
복사
모델 생성 :

IsolationForest 주요 인자 설명

1.
n_estimatores (default: 100)
•
설명: 앙상블에 사용할 트리의 개수를 지정합니다.
•
권장 값: 일반적으로 100~200 사이를 권장합니다.
2.
contamination (default: 'auto')
•
설명: 데이터셋 내에서 예상되는 이상치의 비율을 지정합니다.
◦
0~0.5 사이의 float 값 : 데이터셋에서 이상치로 간주할 비율을 직접 지정 예 : '0.05'는 5%의 데이터를 이상치로 간주
•
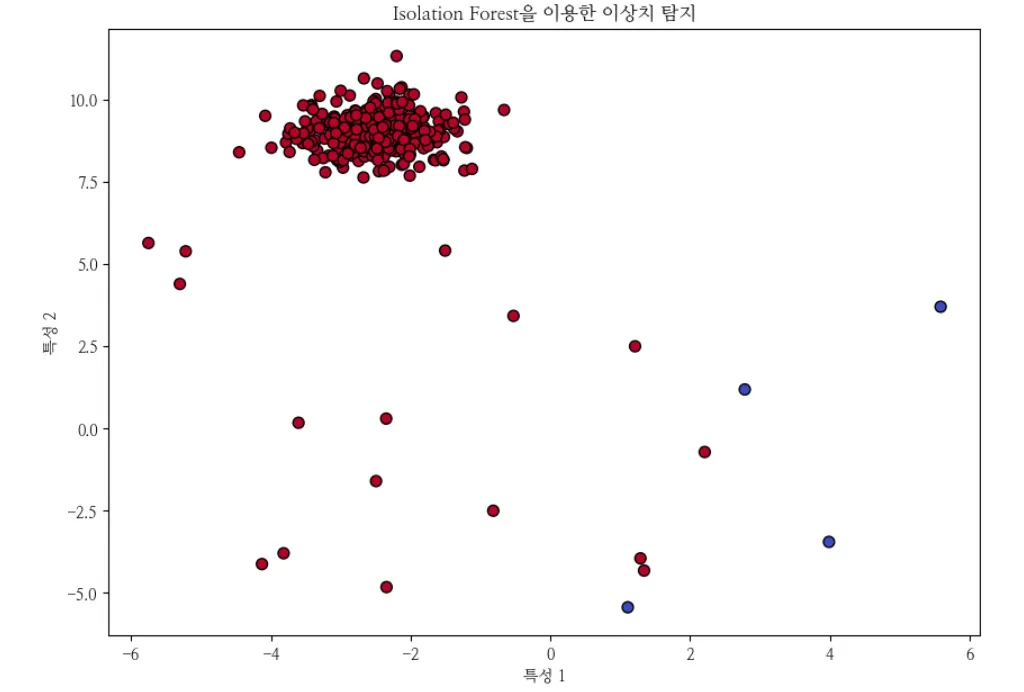
contamination을 0.01로 설정
# contamination을 0.01로 설정 (즉, 1%의 데이터를 이상치로 간주) model = IsolationForest(n_estimators=100, contamination=0.01, random_state=42) model.fit(X) pred = model.predict(X) # 4. 결과 시각화 plt.figure(figsize=(10, 7)) plt.scatter(X[:, 0], X[:, 1], c=pred, cmap='coolwarm', edgecolor='k', s=50) plt.title("Isolation Forest을 이용한 이상치 탐지") plt.xlabel("특성 1") plt.ylabel("특성 2") plt.show()
Python
복사
•
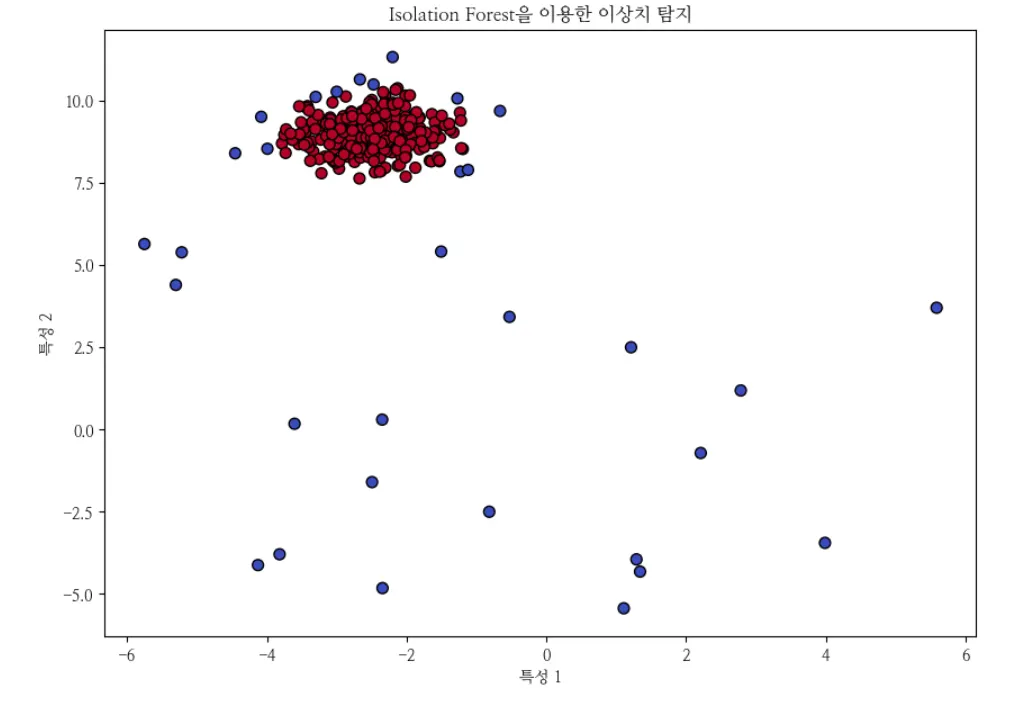
contamination을 0.1로 설정
# contamination을 0.1로 설정 (즉, 10%의 데이터를 이상치로 간주) model = IsolationForest(n_estimators=100, contamination=0.1, random_state=42) model.fit(X) pred = model.predict(X) # 4. 결과 시각화 plt.figure(figsize=(10, 7)) plt.scatter(X[:, 0], X[:, 1], c=pred, cmap='coolwarm', edgecolor='k', s=50) plt.title("Isolation Forest을 이용한 이상치 탐지") plt.xlabel("특성 1") plt.ylabel("특성 2") plt.show()
Python
복사

참고 자료

Made with