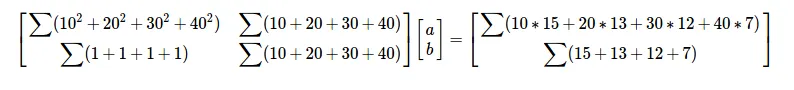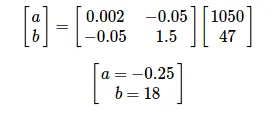.png&blockId=04a8d577-ace8-4bac-bec8-3da8a3f63bbd)
@Jinyeop Kang, 2022-09-29
1. 최소제곱법이란?
•
최소제곱법은 독립 변수와 종속 변수 사이의 관계를 나타내는 최적의 곡선(Best Fit)을 찾는 데 사용되는 방법이다.
•
회귀 분석에서 자료들 사이에서 패턴을 도출해내는데 쓰인다.
•
직관적이고 간단하기에 수치 해석, 회귀 분석 등 다양한 통계적인 접근의 기본이 된다.
•
최소제곱법을 이해하기 위해서는 최적의 곡선을 공식화하는 것과 관련된 개념에 익숙해져야한다.
•
최소제곱법이라는 이름은 얻은 오차의 제곱을 최대한 최소화해야 한다는 발상에서 나왔다.
2. 최적의 곡선이란 무엇인가?
•
최적의 곡선(가장 적합한 선)은 2개 이상의 변수들의 관계를 나타낼 때 그려진다.
•
어떤 데이터가 존재할 때, 해당 데이터 간의 관계를 나타내기 위해 데이터의 산점도(Scatter Plot)에 가장 적합한 선이 그려진다.
•
회귀 분석에서는 예측 변수와 대상 변수 사이의 명확한 관계를 얻기 위해 최소제곱과 같은 수학적인 방법을 사용한다. 최소제곱법은 최적의 곡선을 그리는 가장 효과적인 방법 중 하나이기 때문이다.
•
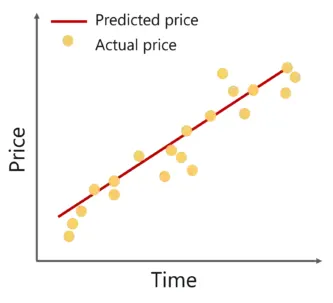
예를 들어, 일정 기간 동안의 회사의 매출을 나타내는 최적의 곡선을 그리면 다음과 같은 그래프의 형태로 표시된다.
•
이 때, 최적의 곡선(Predicted price)은 모든 분산된 데이터 포인트에 가능한 한 가깝다. 이것이 우리가 생각하는 가장 이상적인 최적의 곡선의 모습이다.
•
다음으로는 최적의 곡선을 도출해내는 전체 과정을 더 잘 이해하기 위해 최소제곱법을 이용하여 최적의 곡선을 계산하는 법에 대해서 알아볼 것이다.
3. 최소제곱법의 유도
•
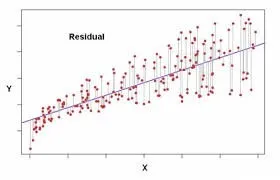
흩뿌려져 있는 자료들과 이 점들 사이에 일관성을 찾기 위해 그래프 f(x)를 가정하자. 이 때, 각 점들(data)과 그래프(line) 간의 차이를 residual (잔차)라고 한다.
•
최적의 곡선을 구하기 위해서는 이 잔차를 최소화해야 한다. 즉, 잔차를 최소화해야 한다는 것은 각 데이터들과 그래프 간의 차이가 가장 최소가 되는 그래프 f(x)를 찾아야 한다는 것을 의미한다.
유도 과정
4. 최소제곱법의 적용 사례
최소제곱법은 다양한 방법에서 활용할 수 있다. 다음은 영지 짜장면 집에서 짜장면 가격이 오르면 얼마나 손님이 줄어드는 지에 관한 표이다. 여기서 최소제곱법을 통해서 가격과 손님간의 상관함수를 도출할 수 있다. (가격 : 독립 변수, 속님 : 종속 변수)
앞선 행렬을 여기 대입을 해보면 다음과 같다.
위 식을 풀어서 계산을 하면 다음과 같다. 최소제곱합이 최소가 되는 방정식은 f(x)는 -0.25x+ 18이다.
References
•
•
•
•
•
•
•
•
•
