한신대학교 AI·SW학과 / 박사과정 2학기 / 최현범
1. 이론적 배경
1.1 MICE는 결측치(missing value)를 대치(imputation)하는 기법 중 하나임
결측치 :
데이터셋에서 누락된 값으로 다양한 이유로 발생하고, 결과에 영향을 줄 수 있어 적절한 처리가 필요
(센서 오작동으로 인한 누락, 측정 범위를 벗어난 경우, 응답자의 질문 답변 누락 등)대치 :
결측치를 추정하여 채우는 과정
통계적 방법이나 알고리즘을 사용하여 적절한 값으로 대치하는 것
이는 데이터의 완전성을 유지하고, 분석의 정확성을 높이기 위해 수행됨
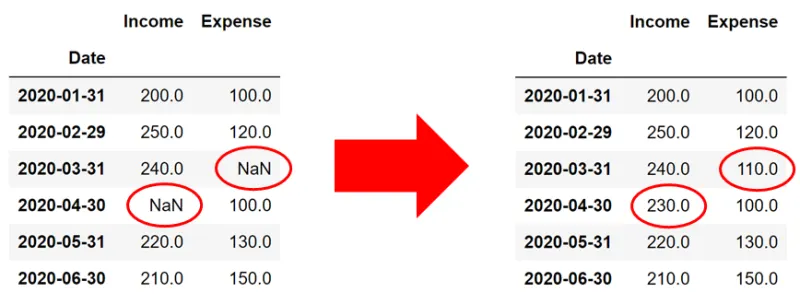
<그림 1 . 결측치 대치의 예시>
일반적인 결측치 대치 시나리오 :1.
결측된 데이터를 식별 (데이터셋에서 값이 없는 부분을 찾아냄)
2.
값을 추정하고 대치 (데이터셋에서 값이 없는 부분에 대치할 값을 넣음)
3.
결측된 데이터가 없는 완전한 데이터셋 완성
3가지 데이터 결측 메커니즘 :3가지 데이터 결측 메커니즘 | 설명 |
완전 무작위 결측 (MCAR, Missing Completely at Random) | 결측 데이터가 다른 어떤 변수와도 관련이 없음 |
무작위 결측 (MAR, Missing at Random) | 결측 데이터가 관측된 다른 변수와 관련 있음
결측된 변수 자체의 값과는 무관 |
비무작위 결측 (MNAR, Missing Not at Random) | 결측이 결측된 변수 자체의 값과 관련이 있음 |
1.
MCAR 예시 :
•
예시: 동전 던지기 게임
•
상황: 100명이 동전 던지기 게임을 하는데, 기록하는 사람이 무작위로 10명의 결과를 깜빡하고
기록하지 않은 경우
→ 완전히 우연에 의해 발생됨
2.
MAR 예시 :
•
예시: 소득 수준 관련 설문조사
•
상황: 저소득 응답자들이 수입 관련 설문 문항에 답변을 꺼리는 경우
→ 이 경우, 수입 데이터의 결측은 응답자의 직업이나 교육 수준과 관련이 있을 수 있음
3.
MNAR 예시 :
•
예시: 우울증 설문
•
상황: 우울증 환자들이 우울증 정도를 묻는 설문에 응답하지 않는 경우
→ 이 경우 우울증 점수 데이터의 결측은 실제 우울증의 심각도와 직접적으로 관련이 있음
1.2 MICE는 다중 대치(Multiple Imputation)를 주로 수행함
단순 대치(Simple Imputation)의 한계를 극복하기 위해 다중 대치가 개발되었음
단순 대치 :결측치를 단일 값(평균(mean)이나 중앙값(median) 등 하나의 값)으로 대치하는 기본적인 방법
1.
평균 대치 (Mean Imputation)
•
방법 : 결측값을 해당 변수의 평균값으로 대치
•
예시 : '연봉' column에서 몇몇 직원의 연봉 정보가 누락되었다면, 전체 직원의 평균 연봉으로
누락된 값을 채움
•
장점 : 간단하고 빠르게 적용할 수 있음
•
단점 : 데이터의 분산(퍼짐 정도)을 줄이고, 변수 간의 관계를 왜곡할 수 있음
(경력이 5년인 직원과 경력 10년인 직원이 동일하게 평균 연봉을 받는 것으로 표현되어
경력과 연봉의 관계가 왜곡됨)
2.
중앙값 대치 (Median Imputation)
•
방법 : 결측값을 해당 변수의 중앙값으로 대치
•
예시 : '나이' column에서 일부 데이터가 누락되었다면, 전체 나이 데이터의 중앙값으로
누락된 값을 채움
•
장점 : 극단값*(outliers)의 영향을 덜 받습니다.
•
단점 : 평균 대치와 유사하게 데이터의 특성을 왜곡할 수 있습니다.
(경력을 나타낸 데이터가 누락되었을 때, 중앙값인 10년으로 대치하여
10년의 경력을 가진 직원의 비중이 실제보다 높게 나올 수 있음)
3.
최빈값 대치 (Mode Imputation)
•
방법 : 결측값을 해당 변수의 최빈값(가장 자주 나타나는 값)으로 대치
•
예시 : '직급' column에서 일부 데이터가 누락되었다면, 가장 많이 나타나는 직급으로 누락된 값을 채움
•
장점 : 범주형 변수에 특히 유용하며, 데이터의 분포를 크게 변화시키지 않음
•
단점 : 연속형 변수에는 적합하지 않을 수 있으며, 다양성을 감소시킬 수 있음
('부서' 데이터에 누락된 값이 발생되었을 때, 최빈값인 '영업부'로 대치하면
실제보다 영업부 직원의 비율이 과대평가될 수 있음)
4.
보간법 (Interpolation)
주로 시계열 데이터나 순서가 있는 데이터에서 사용됨
•
선형 보간 (Linear Interpolation) :
결측값 전후의 두 점을 직선으로 연결하여 그 사이의 값을 추정함
단순하고 계산이 빠르지만, 복잡한 패턴을 포착하기 어려움
•
스플라인 보간 (Spline Interpolation) :
선형 보간보다 더 부드러운 곡선을 사용함
여러 개의 다항식을 이어 붙여 전체적으로 부드러운 곡선을 만듬
비선형적인 패턴을 더 잘 포착할 수 있음
평균 대치법의 단점에 대한 예시
즉, 예측값을 사용할 때는 그 값에 불확실성이 존재한다는 점을 꼭 고려해야 함
(그 값이 정확하지 않다는 것)
이러한 단점(데이터의 불확실성)들로 인해, 실제 데이터 분석에서는 이런 단순한 대치 방법보다 더 복잡하고 정교한 방법들을 사용하는 경우가 많음
예를 들어, 다중 대치이나 고급 머신러닝 기법을 활용하여 데이터의 불확실성을 더 잘 반영하고
원래의 분포를 보존하려고 함.
(결측치를 채운 후에도 데이터의 전체적인 통계적 특성(평균, 분산, 상관관계 등)을 유지하려는 노력)
다중 대치 :다중 대치는 결측치를 처리하는 더 정교한 방법으로, 단순 대치의 한계를 극복하고자 개발되었음
결측치를 여러 번 대치하여 여러 개의 완전한 데이터셋을 생성한 후, 이를 결합하여 분석하는 방법임
•
여러 번의 대치: 결측치를 단 한 번이 아니라 여러 번(보통 5~10회, 상황에 따라 다름) 대치함
•
불확실성 반영: 각 대치 시 약간의 무작위성을 추가하여 불확실성을 반영함
•
편향 감소: 단순 대치법에 비해 추정치의 편향을 줄임
•
정확한 표준오차: 결측으로 인한 불확실성을 표준오차 계산에 반영함
•
분석: 각 대치된 데이터셋에 대해 원하는 분석을 수행함
•
결과 통합: 여러 분석 결과를 통합하여 최종 결론을 도출함
다중 대치 종류 :방법 | 설명 | 특징 |
다변량 정규분포 대치 (MVNI) | 데이터가 다변량 정규분포를 따른다고 가정하고 결측값을 대치 | 데이터가 정규분포를 따를 때 유용 |
연쇄방정식에 의한 다중대치 (MICE)* | 각 변수에 대해 별도의 회귀 모델을 사용하여 결측값을 대치 | 각 변수의 결측값을 연쇄적으로
대치하며 반복 수행 |
예측 평균 매칭 (PMM) | 예측 모델을 사용하여 결측값을
대치하고, 예측값과 가장 가까운 관측값을 선택하여 대치 | 변수의 유효한 범위 내에서 값을 산출하는 데 유리 |
Markov Chain Monte Carlo (MCMC) | 베이지안 접근법을 사용하여 결측값을 대치 | 결측값의 분포를 추정하고 샘플링하여 대치값 생성 |
다중 대치의 단계 :
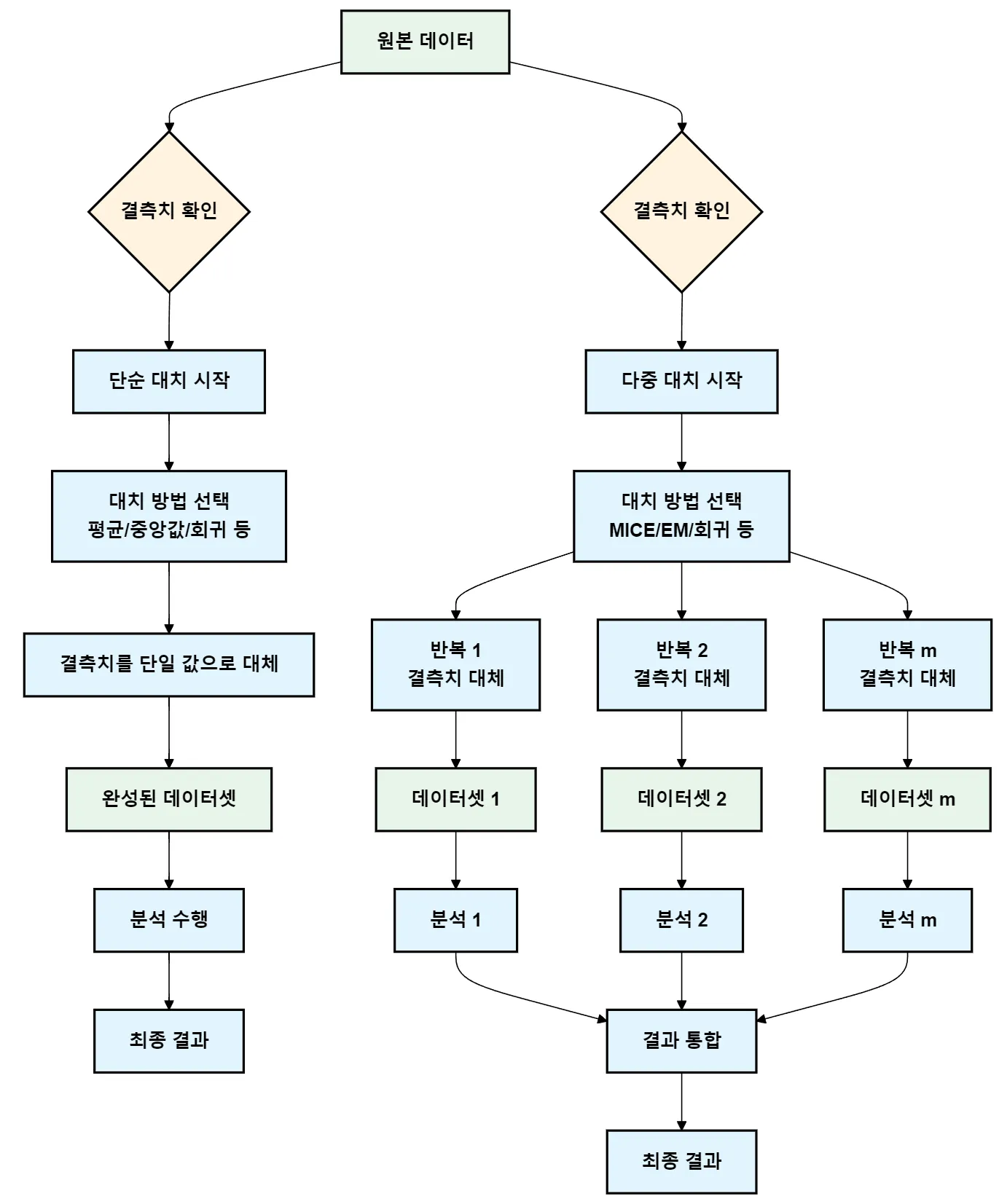
<일반적인 단순 대치와 다중 대치의 상세 단계>
1.
대치 (Imputation) 단계:
•
결측값에 대해 m(반복 횟수)개의 가능한 값을 생성합니다 (보통 m = 5~10).
•
각 대치값은 온전한 데이터와 결측값이 생긴 이유를 바탕으로 생성됩니다. (데이터와 결측값이 생긴 이유를 분석하고 이에 따라 모델 선택, 반복 회수 설정)
2.
분석 (Analysis) 단계:
•
각 대치된 데이터셋에 대해 원하는 통계 분석을 수행합니다.
•
이 과정에서 m개의 서로 다른 분석 결과가 얻어집니다.
3.
풀링 (Pooling) 단계:
•
m개의 분석 결과를 결합하여 최종 추정치와 표준오차를 계산합니다.
•
Rubin의 규칙을 사용하여 결과를 통합합니다.
Rubin’s Rules :다중 대치에서 여러 개의 대치된 데이터셋으로부터 얻은 분석 결과들을 하나로 통합하는 방법.
1.
최종 추정치 계산:
•
여러 대치된 데이터셋의 추정치들의 평균을 구하는 단계.
•
θ̂ = (1/m) Σ θ̂ᵢ:
◦
θ̂: 최종 추정치
◦
m: 데이터셋 개수
1.
여러 개의 대치된 데이터셋 각각의 평균값(추정치)을 구합니다.
2.
이 값들을 모두 더해서 데이터셋의 개수(m)로 나눕니다.
3.
각 데이터셋에서 나온 평균값들의 평균이 최종 추정치(θ̂)가 됩니다.
2.
내부 분산(W)와 데이터셋 간 분산(B):
•
각 데이터셋의 내부 분산(W)과 데이터셋 간 분산(B)을 구하는 단계.
•
W = (1/m) Σ Wᵢ:
◦
각 데이터셋 내부의 분산들의 평균(W)
•
B = (1/(m-1)) Σ (θ̂ᵢ - θ̂)²:
◦
(1/(m-1))는 데이터셋 간의 분산을 계산할 때 필요한 보정 값입니다.
◦
Σ (θ̂ᵢ - θ̂)²는 각 데이터셋의 추정치(θ̂ᵢ)와 최종 추정치(θ̂) 간의 편차의 제곱을 의미합니다.
3.
최종 분산 계산:
•
V = W + (1 + 1/m)B:
◦
내부 분산과 데이터셋 간 분산을 더해서 최종 분산(V)을 계산합니다.
◦
(1 + 1/m) 부분은 대치된 데이터셋의 수를 고려한 보정 값입니다.
4.
활용
•
최종 추정치는 데이터 분석, 모델 제작 등 다양한 분야에 활용될 수 있음.
•
분산을 활용하여 결과의 신뢰성과 불확실성을 분석할 수 있어 더 정확한 결정을 내릴 수 있음
→ 단순 대치를 보완한 방법임.(불확실성 반영, 원래 분포 유지하려는 노력)
1.3 다중 대치를 이용가능한 모델 기반 대치(model-based imputation)
모델 기반 대치법 :•
결측값을 예측하기 위해 통계적 모델이나 기계 학습 모델을 사용하는 방법임
•
이러한 방법들은 단순 대치와 다중 대치 모두에 사용될 수 있음
(간단하게 한번 만하면 단순 대치, 여러 번 반복하면 다중 대치)
<단순 대치와 다중 대치의 차이>
모델 기반 대치법
모델 기반 대치법 중 MICE 알고리즘이 있음
MICE 알고리즘도 이론 상 단순 대치가 가능하지만, 다중 대치를 목적으로 개발되었음.
1.4 MICE 알고리즘
•
MICE는 다중 대치 중 가장 널리 사용되는 알고리즘임
•
특히 복잡한 결측 패턴을 가진 다변량 데이터에 효과적임
MICE는 평균(mean)이나 중앙값(median) 등 하나의 값으로 결측값을 채워넣는 단순 대치법과 달리, 각 변수의 결측값을 다른 모든 변수를 사용하여 예측함
→ 각 변수마다 결측값을 예측하고 그 예측 값을 사용해서 다른 변수의 결측값도 채워가는 방식(반복)
→ 이렇게 연쇄적으로 계산되어 Multiple Imputation by Chained Equations Algorithm임
→ 연쇄적으로 예측을 반복해서 각 변수의 결측값을 점진적으로 더 정확하게 채워나가는 방식
2. 동작 원리
2.1 MICE 알고리즘의 자세한 동작원리
누락된 데이터를 연쇄방정식으로 여러 번 채우는 방식으로 작동함
예측 모델을 기반으로 반복적으로 결측치를 대치하여 수렴하는 알고리즘
단계 상세
MICE 알고리즘 동작 단계
1.
초기 대치:
결측 값을 초기 대치(각 변수별 평균, 중앙값, 또는 다른 방법)로 대치
예: 키, 체중, 나이 -> 각 3종류의 변수가 있다고 가정하고, 각 결측치를 각각의 데이터의 평균이나 중앙값으로 초기 대치. (키끼리, 체중끼리, 나이끼리)
2.
회귀 모델:
각 결측 변수를 종속 변수로 설정하고, 나머지 변수를 예측 변수로 사용해 회귀 모델 생성
예: 키를 종속 변수로 설정하고, 체중과 나이를 예측 변수로 사용해 결측된 키 값을 예측하는 모델 생성
총 3개의 회귀 모델을 사용해 각 변수를 대치. (변수가 10개라면 회귀 모델도 10개가 필요)
3.
순차적 대치:
첫 번째 변수의 결측 값을 예측한 후, 예측된 값으로 대치
업데이트된 데이터를 사용해 다음 변수의 결측 값을 예측하고, 이 과정을 반복해 모든 변수를 대치
예: 키를 먼저 대치한 후, 체중, 그 다음 나이를 대치하는 식으로 순차적으로 진행
이렇게 해서 하나의 대치 데이터셋(X1이라고 가정)을 완성
MICE는 가장 처음으로 구한 변수의 결측값은 초기 대치로 학습한 회귀 모델로 얻은 값이므로 가장 부정확할 수 있음. 하지만 순차적으로, 반복적으로 더 정교한 예측값을 얻는 방법임
4.
다중 대치:
대치 반복마다 새로 대치된 값(X1)을 기반으로 회귀 모델을 다시 학습하고, 결측값을 예측해서 대치하는 과정을 반복 (일반적으로 5~10회 반복 -> 반복 횟수에 따라 데이터셋 개수가 정해짐)
예: X1-> X2, X2 -> X3, X3 -> X4.....
5.
결합 및 분석:
다중 대치 데이터셋을 사용하여 각각의 분석을 수행
결과를 결합하여 최종 분석 결과를 도출. 이 과정에서 결측 데이터의 불확실성을 평가할 수 있음. (Rubin's Rules)
이러한 순서로 진행됨.
2.2 MICE의 주요 특징
1.
유연성: 각 변수의 특성에 맞는 회귀 모델을 선택할 수 있음. 예를 들어:
•
연속형 변수: 선형 회귀
•
이진 변수: 로지스틱 회귀
•
범주형 변수: 다항 로지스틱 회귀
•
계수형 변수: 포아송 회귀
2.
변수간 관계 보존: 각 변수를 다른 모든 변수의 함수로 모델링하므로, 변수 간의 복잡한 관계를 잘 보존합니다. → 앞서 설명한 연쇄방정식
3.
결측 메커니즘 처리: MAR(Missing At Random) 가정 하에서 잘 작동하며, 때로는 MNAR(Missing Not At Random) 상황에서도 적용 가능함
4.
불확실성 반영: 여러 대치 데이터셋을 생성함으로써 대치 과정의 불확실성을 반영함
5.
유연성 : 다양한 유형의 변수와 분석 모델에 적용할 수 있음
6.
편향 감소 : 단일 대치법에 비해 추정치의 편향을 크게 줄일 수 있음
2.3 MICE 사용 시 고려사항
1.
계산 비용: 복잡한 데이터셋에서는 계산 시간이 길어질 수 있음
2.
수렴 확인: 알고리즘의 수렴을 그래프로 확인하는 것이 중요 → 알고리즘이 잘 작동하는 지 확인
(여러 번의 반복 후에 결과값이 안정적으로 일정한 값을 가지는 것을 시각적으로 확인하는 것)
3.
변수 선택: 대치 모델에 포함할 변수를 신중히 선택해야 함
너무 많은 변수를 포함하면 과적합의 위험이 있음
(중요한 변수만을 선택하는 것이 필요)
4.
상호작용과 비선형성: 필요한 경우 상호작용 항이나 비선형 항을 모델에 포함시켜야 함
상호작용 항: 두 변수 간의 관계를 모델에 반영
비선형 항: 변수 간의 곡선형 관계를 반영
→ 데이터를 더 정확하게 예측하고 복잡한 관계를 잘 유지할 수 있음
(결국 이전에 대치했던 특정 변수를 이후 회귀 모델에 적용하기 위해 설정하는 것임)
예시를 통한 설명
5.
결측 메커니즘의 가정: MICE는 결측 데이터가 MAR(Missing At Random)이라는 가정을 전제로함. 만약 결측 메커니즘이 다르다면, MICE 결과의 신뢰성이 떨어질 수 있음
3. 코드 구현 및 데모
# 필요한 라이브러리 임포트
import pandas as pd # 데이터 처리를 하기 위함
import numpy as np # 수치 계산을 하기 위함
import matplotlib.pyplot as plt # 그래프를 통한 시각화를 위함
from sklearn.impute import SimpleImputer # 초기 대치를 위한 단순 대치
from sklearn.experimental import enable_iterative_imputer # IterativeImputer를 사용하기 위해 필요
from sklearn.impute import IterativeImputer #sklearn에 구현된 MICE 알고리즘
from sklearn.linear_model import LinearRegression # 회귀 모델을 위한 LinearRegression 임포트
# sklearn은 파이썬에서 사용되는 데이터 분석 및 기계 학습용 오픈소스 라이브러리임
# 1. 샘플 데이터 생성
np.random.seed(0) # 재현 가능한 결과를 위해 랜덤 시드 설정
df = pd.DataFrame({
'A': [1, 2, np.nan, 4, 5, 6, np.nan, 8, 9, 10],
'B': [np.nan, 2, 3, 4, 5, np.nan, 7, 8, 9, 10],
'C': [1, 2, 3, np.nan, 5, 6, 7, 8, np.nan, 10]
}) # 결측치(np.nan)가 포함된 데이터프레임 생성
print("1. 원본 데이터:") # 원본 데이터 출력
print(df) # 데이터프레임 df 출력
Python
복사
# 2. 초기화 단계: SimpleImputer를 사용하여 평균으로 결측치 대치
mean_imputer = SimpleImputer(strategy='mean') # 평균값으로 대치하는 SimpleImputer 객체 생성
mean_imputed = pd.DataFrame(
mean_imputer.fit_transform(df), # fit_transform 메서드로 결측치를 평균값으로 대치
columns=df.columns # 원본 데이터프레임의 열 이름 유지
)
print("\n2. 초기화 후 데이터 (평균 대치):") # 평균값으로 초기화(결측치 대치) 후 데이터를 출력
print(mean_imputed) # 평균 대치 후 데이터프레임 출력
Python
복사
# 3. MICE 알고리즘 적용
mice_imputer = IterativeImputer(
estimator=LinearRegression(), # 선형 회귀를 사용하여 결측치 예측
max_iter=10, # 최대 반복 횟수 설정
random_state=0 # 재현 가능한 결과를 위해 랜덤 시드 설정
)
mice_imputed = pd.DataFrame(
mice_imputer.fit_transform(df), # fit_transform 메서드로 MICE 알고리즘 적용
columns=df.columns # 원본 데이터프레임의 열 이름 유지
)
print("\n3. MICE 적용 후 최종 데이터:") # MICE 적용 후 데이터를 출력
print(mice_imputed) # MICE 알고리즘 적용 후 데이터프레임 출력
# 단순대치법 (중앙값) 적용 -> MICE 알고리즘과 비교하기 위함
median_imputer = SimpleImputer(strategy='median') # 중앙값으로 대치하는 SimpleImputer 객체 생성
median_imputed = pd.DataFrame(
median_imputer.fit_transform(df), # fit_transform 메서드로 결측치를 중앙값으로 대치
columns=df.columns # 원본 데이터프레임의 열 이름 유지
)
print("\n단순대치법 (중앙값) 적용 후 데이터:") # 단순대치법 적용 후 데이터를 출력
print(median_imputed) # 중앙값 대치 후 데이터프레임 출력
Python
복사
# 분산 비교
print("\n분산 비교:")
print("원본 데이터 분산:")
print(df.var()) # 원본 데이터의 분산 계산
print("\n평균 대치법 분산:")
print(mean_imputed.var()) # 평균 대치 후 데이터의 분산 계산
print("\n중앙값 대치법 분산:")
print(median_imputed.var()) # 중앙값 대치 후 데이터의 분산 계산
print("\nMICE 대치법 분산:")
print(mice_imputed.var()) # MICE 대치 후 데이터의 분산 계산
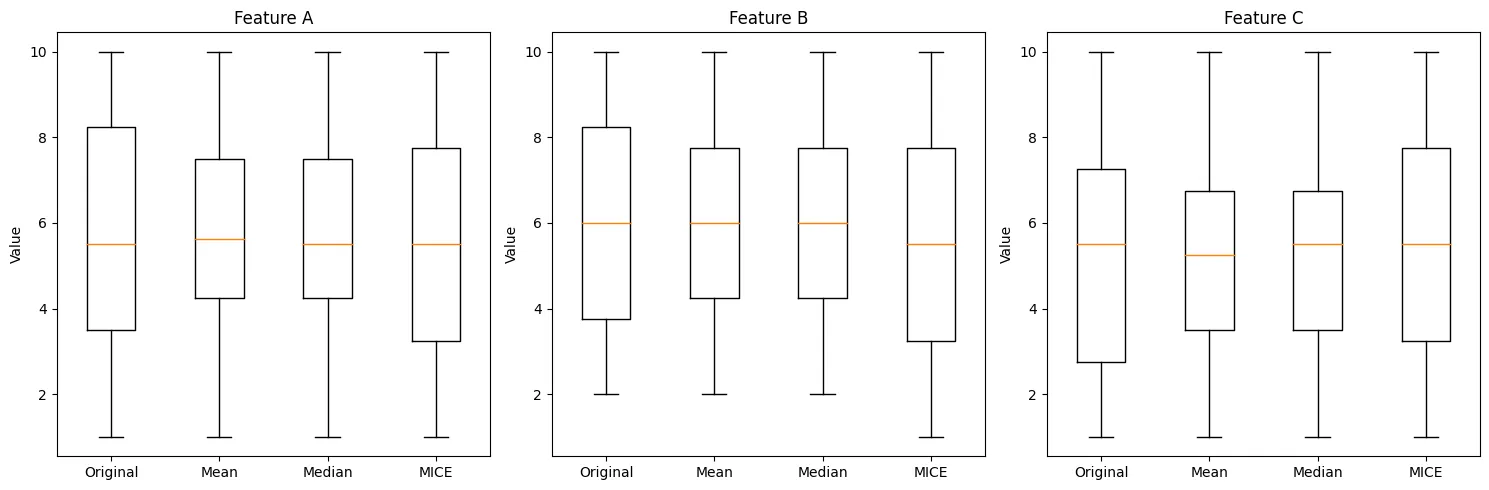
# 시각화: 박스플롯
plt.figure(figsize=(15, 5)) # 그래프 크기 설정
for i, col in enumerate(df.columns):
plt.subplot(1, 3, i+1) # 1행 3열의 서브플롯 생성
data = [df[col].dropna(), mean_imputed[col], median_imputed[col], mice_imputed[col]]
plt.boxplot(data, labels=['Original', 'Mean', 'Median', 'MICE'])
plt.title(f'Feature {col}')
plt.ylabel('Value')
plt.tight_layout() # 서브플롯 간 간격 조정
plt.show() # 그래프 표시
Python
복사
각 특성 별 분석 :Feature A:
•
MICE 방법이 원본 데이터의 분포와 가장 유사해 보임
•
평균과 중앙값 대치는 원본보다 분포 범위가 좁음
Feature B:
•
세 가지 대치 방법 모두 원본과 유사한 분포를 보임
•
MICE가 원본의 이상치 패턴을 가장 잘 유지하고 있음
Feature C:
•
MICE 방법이 원본 데이터의 분포와 가장 유사함
•
평균과 중앙값 대치는 원본보다 분포 범위가 좁아졌음
전체적인 결론:
•
MICE 방법이 세 특성 모두에서 원본 데이터의 분포를 가장 잘 보존하는 것으로 보임
→ 데이터의 불확실성을 고려하고 분포 유지가 됨
•
평균과 중앙값 대치는 데이터의 변동성을 줄이는 경향이 있어, 원본 데이터의 특성을 일부 손실시킬 수 있음. → 데이터의 불확실성을 고려하지 않음, 분포 유지가 안된 결과임
참고자료
5.
챗봇 활용(Copilot, Claude)
