Search
moon
sun

Decision Tree (의사결정나무)

, @6/28/2022, , @2/24/2023
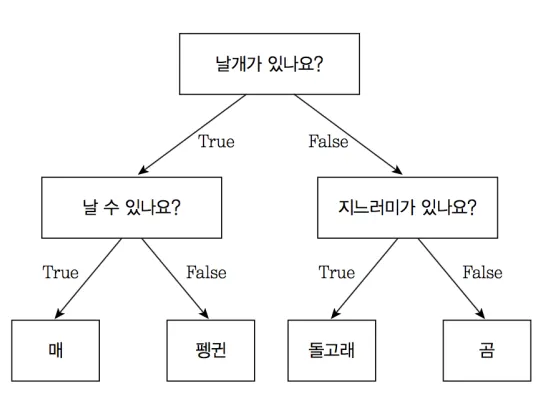
: 트리 구조의 형태로 모델을 생성하는 머신 러닝 알고리즘
•
특정 조건을 기준으로 결론에 도달할 때까지 연속적인 ‘예/아니오’ 질문들을 반복해 분류/회귀를 진행하는 분류/회귀 데이터 마이닝 기법
•
데이터를 불균형하게 나누는 것이 목적임
•
종속 변수의 형태에 따라 분류와 회귀 문제로 나뉨

기본 용어

•
Node (노드): 트리를 구성하는 단위 개체. 데이터를 분리하기 위한 조건을 가짐
◦
Root Node: 트리의 최상위 노드
◦
Leaf Node (= Terminal Node): 트리의 끝에 위치한 노드 (Child Node를 가지지 않음)
◦
Internal Node: 트리의 중간에 위치한 노드
◦
Parent Node: 특정 노드의 상위 노드
◦
Child Node: 특정 노드의 하위 노드
•
Branch (가지): 특정 노드에서 파생되는 트리 부분
•
Depth (깊이): 트리의 계층 수
•
Pure : 노드에 의해 분리된 데이터가 모두 같은 클래스일 경우
◦
Decision Tree 알고리즘은 기본적으로 Pure 한 Leaf Node 들을 만드는 방식으로 동작
•
Impure: 노드에 의해 분리된 데이터에 여러 클래스가 존재할 경우

특장점

•
변수와 임계치의 조합으로 표현된 조건을 통해 데이터를 분할하는 구조이므로, 학습된 모델을 설명하기 쉬움
•
불순도 (impurity) 를 기반으로 각 변수의 중요도를 모델 학습 과정에서 자동 계산 → 모델 해석 및 변수 선택에 활용 가능
•
비모수적 모델: 통계적 가정으로부터 자유로움
•
주요 앙상블 기법의 기본 모델, 예: Random Forest, Gradient Boosting Machine
•
데이터 규모가 작은 경우, 성능이 불안정할 가능성 높음
•
과대적합(overfitting)되기 쉬움 → Pruning (가지치기) 또는 Depth 제한이 필요
•
회귀 문제에 적용할 경우 값을 구간화(연속적→비연속적)하여 처리

주요 유형

•
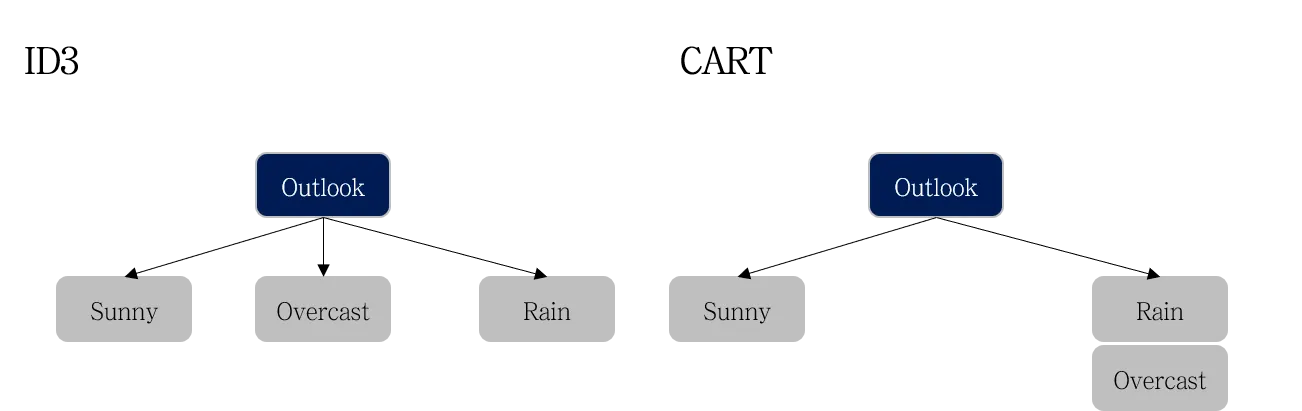
CART (Classification And Regression Tree, Brieman et. al, 1984)
◦
Binary Tree : 조건의 결과가 True/False로 나뉘며, 두 개의 자식 노드를 생성 (if 조건문과 비슷)
◦
트리 생성을 위해 Gini Index 사용
•
ID3 (Iterative Dichotomiser 3, Quinlan, 1986)
◦
모든 클래스 별로 가지를 생성
◦
모든 변수가 범주형인 데이터셋에만 적용 가능
◦
트리 생성을 위해 Entropy & Information Gain 사용
그림. ID3와 CART 알고리즘 비교 (출처: Yang, T.)

의사결정나무 모형 생성 절차

1.
Tree Growing (성장) : 최대 크기의 나무 모형을 형성
•
각 마디에서 적절한 최적의 분리 규칙을 찾아 나무를 성장시키는 과정으로 적절한 정지 규칙을 만족하면 중단
2.
Pruning (가지치기) : 최대 크기의 나무 모형에서 불필요한 가지를 제거하여 subtrees (부분 트리)의 집합을 탐색
3.
최적 나무 모형 선택 : 가지치기의 결과인 나무 모형의 집합에서 최적의 모형을 선택
4.
해석 및 예측 : 구축된 나무 모형을 해석하고 예측 모형을 설정한 후 예측에 적용

Impurity (노드의 불순도)

의사결정나무를 구성하는 노드의 데이터 분리 성능을 평가하는 기준으로 모형 생성 과정에서 impurity가 가장 낮은 변수 및 임계치를 탐색하여 그 결과를 노드로 생성
•
불순도 측정 지표(분류): Gini(지니지수), Entropy(엔트로피)
•
불순도 측정 지표(회귀): MSE(평균제곱오차)

Impurity 계산: Classification Tree

Classficiation Tree 에서 Impurity 는 아래와 같이 노드에 의한 데이터 분리 결과에 따라 값이 결정됨
•
여러 클래스의 데이터가 골고루 존재할 경우(예: 50% | 50%): Impurity 값 ↑\uparrow
•
대다수의 데이터가 같은 클래스일 경우(예: 95% | 5%): Impurity 값 ↓\downarrow
Impurity 는 Decision Tree 알고리즘 별로 다른 방식으로 측정됨
•
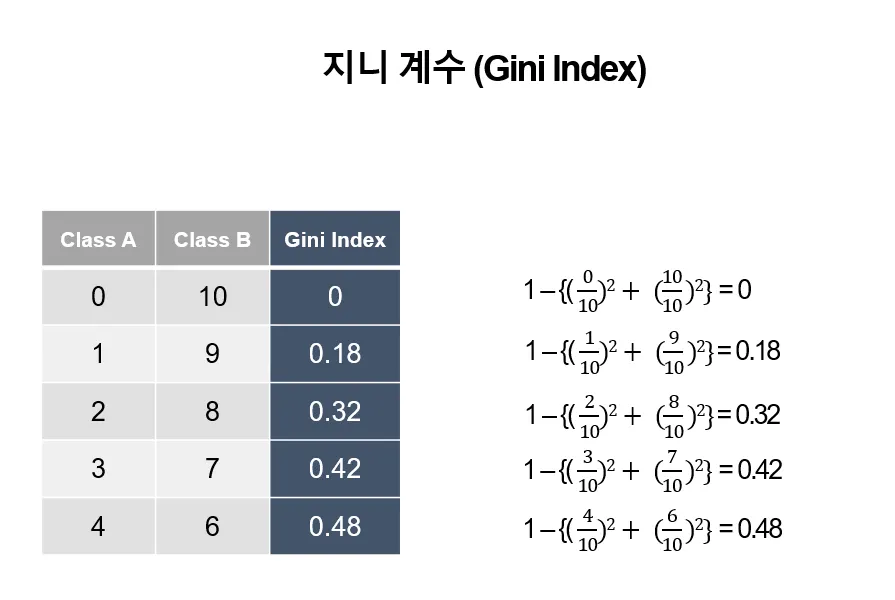
Gini Index (지니 지수): CART 에서 불순도 계산에 사용됨
◦
SS : 특정 노드
◦
cc : 클래스 개수
◦
pip_i : 클래스 ii 의 확률
◦
G(S)→0.5G(S)\rightarrow 0.5 : 해당 노드의 분리 결과가 완전한 불균형 (Impure: 불순도가 높음)
◦
G(S)→0G(S)\rightarrow 0 : 해당 노드의 분리 결과가 완전한 불균형 (Pure: 불순도가 낮음)
G(S)=1−∑i=1c(pi)2G(S)=1-\sum_{i=1}^{c}{(p_i)^2}
노드 분할에서의 지니 계수 계산 예(link)
•
Entropy and Information Gain (엔트로피, 정보 이득): ID3 에서 불순도 계산에 사용됨
엔트로피는 다음의 수식과 같이 계산됨
◦
SS : 특정 노드
◦
cc : 클래스 개수
◦
pip_i : 클래스 ii 의 확률
E(S)=−∑i=1cpilog2piE(S)=-\sum_{i=1}^{c}{p_{i}log_{2}p_{i}}
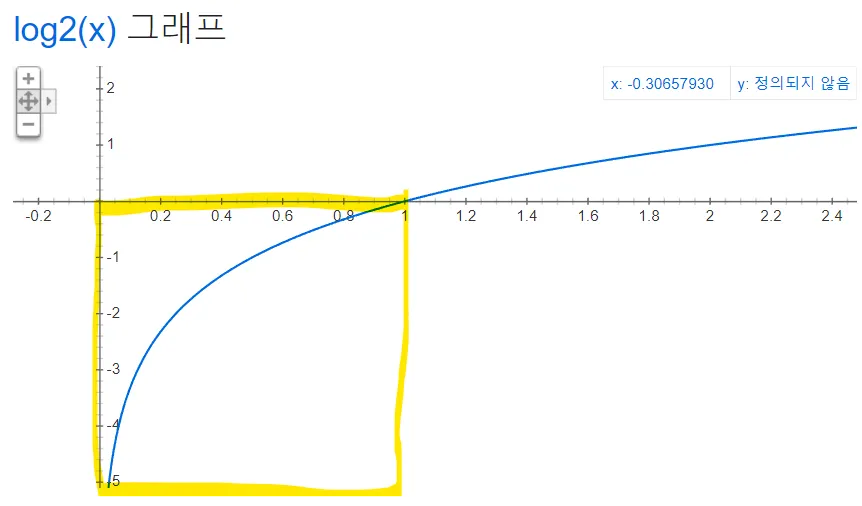
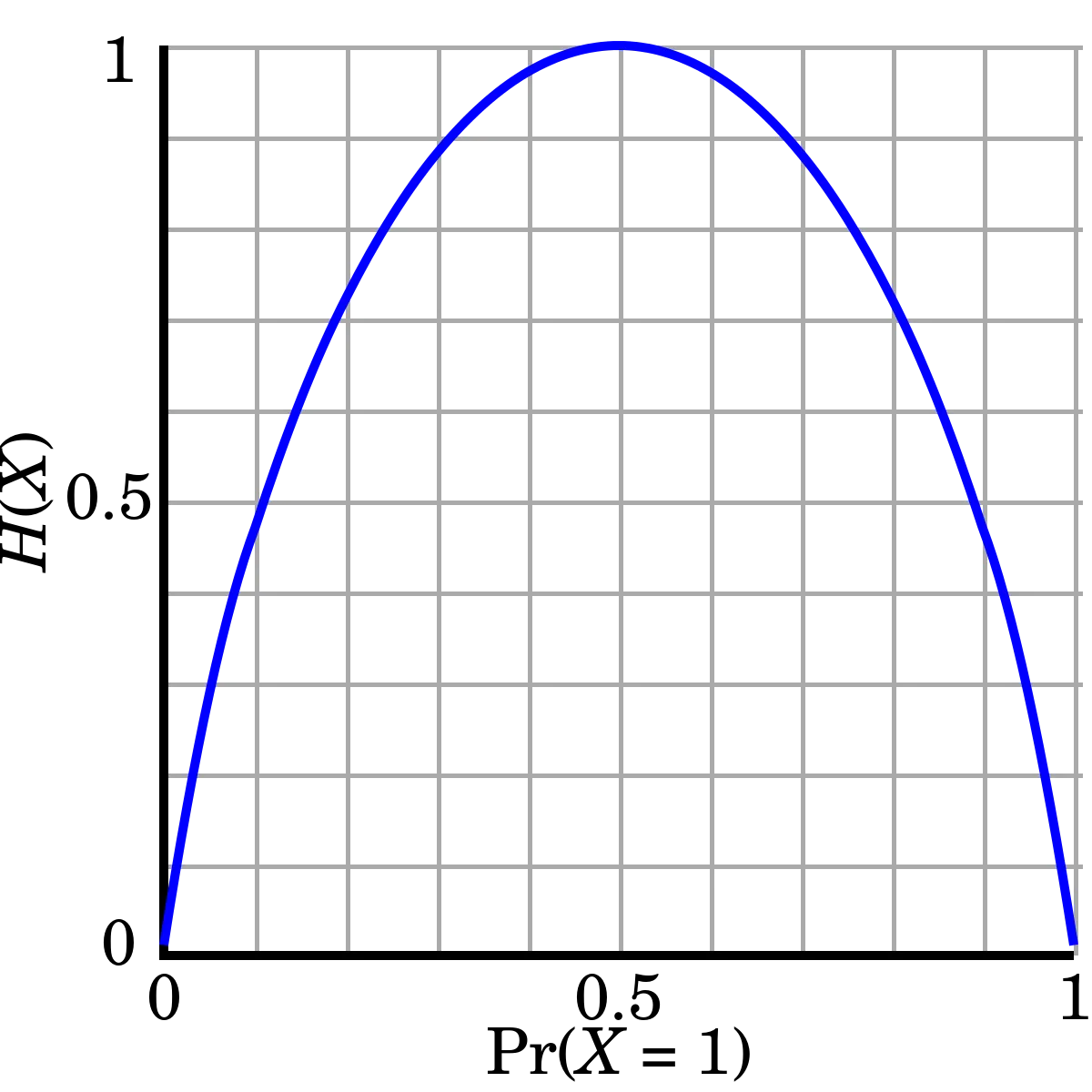
pip_i 가 확률이므로 [0,1][0,1] 범위에서 값을 가지며, 해당 범위에서 log2(pi)log_2(p_i) 는 [−∞,0][-\infty,0] 범위를 가짐
따라서, 수식의 마이너스 기호(−-)에 의해 최종 엔트로피 값을 양수로 표현
log2(pi)log_{2}(p_i) 앞에 pip_i 를 곱하기 때문에 최종 엔트로피 E(S) E(S) 값은 [0,1][0, 1] 범위를 가짐
엔트로피 함수(출처: wikipedia)
•
Information Gain: 분할 전후의 엔트로피 차이
InformationGain=Entropybefore−EntropyafterInformation Gain=Entropy_{before}-Entropy_{after}

Impurity 계산: Regression Tree

Regression Tree 에서 Impurity 는 MSE (Mean Squared Error) 또는 MAE (Mean Absolute Error) 와 같은 오차 함수를 기반으로 계산됨
•
부모 노드 대비 오차가 많이 감소하는 경우: Impurity 값 ↓\downarrow
•
부모 노드 대비 오차가 적게 감소하는 경우: Impurity 값
•
MSE (평균제곱오차)
MSE(t)=1nt∑i=1nt(yi(t)−yˉt)2.\text{MSE}(t) = \frac{1}{n_t} \sum_{i=1}^{n_t} (y_i(t) - \bar y_t)^2.
의사결정나무 회귀 모형 예시

References

•
1.10. Decision Trees, scikit-learn 1.2.1 API Documentation (link)
•
StatQuest, Decision and Classification Trees, Clearly Explained!!!, YouTube (link)
•
z_ai, Decision Trees Explained, Towards Data Science (link)
•
Subramanian, D., Decision Tree in Layman’s Terms, Towards Data Science (link)
•
김진석, 10 장 의사결정나무(tree model), 데이터과학 (link)
•
SH의 학습노트, Decision Tree(의사결정나무) 모형 - Classification/Regression Tree의 직관적/수학적 이해, 티스토리 (link)
•
heeee__ya, 결정트리(Decision Tree) - 기본구조와 CART, ID3 알고리즘, 티스토리 (link)
1.
Decision Tree 시각화 코드(graphviz)
•
Yang, T., 의사결정 나무 (Decision Tree) CART 알고리즘 설명, GitHub (link)
•
ratsgo, 의사결정나무(Decision Tree), GitHub (link)
•
Park, T., 의사결정나무(Decision Tree)의 사용이유, 장단점, 모델평가방법, 변수 중요도 산출방법, 티스토리 (link)
Made with Oopy