- 소리의 물리적 특성과 디지털 표현 -
한신대학교 AI·SW학과 / 박사과정 2학기 / 최현범
1. 이론적 배경
1.1 소리의 물리적 특성
소리(Sound)의 정의•
공기를 구성하는 입자들이 진동하는 현상
•
공기 입자들의 진동이 전파되는 과정
•
매질(공기)의 역할
◦
진동을 전달하는 매개체임
◦
매질 없이는 소리가 전파될 수 없음 (진공 상태)
◦
공기보다 물질의 밀도가 높은 물에서는 소리가 초속 1480 m로 훨씬 더 빠르게 이동
음압(Sound pressure)•
공기의 진동을 측정하는 양적 기준 (공기의 진동으로 인한 압력 변화)
•
단위 : 데시벨(dB)
•
측정 범위 :
◦
0 dB : 인간이 들을 수 있는 가장 작은 소리
◦
30 dB : 조용한 도서관
◦
60 dB : 일반적인 대화
◦
90 dB : 지하철 소음
◦
130 dB : 통증을 유발하는 소리
1.2 사운드 데이터의 이해
사운드 데이터 정의•
시간에 따른 음압의 변화를 기록한 시계열 데이터
시계열 데이터로서의 의미•
시간에 따른 음압의 변화를 기록
•
파형(Waveform)으로 표현 가능
•
디지털 오디오의 기본 데이터 형태
시계열 데이터의 특성•
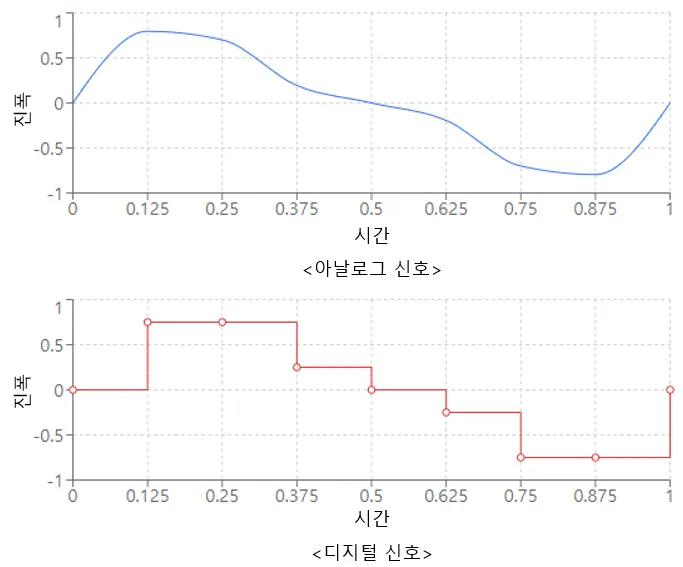
연속적 신호(Continuous Signal)
◦
아날로그 신호
◦
시간에 따라 끊김 없이 변화
◦
무한한 정밀도를 가짐
◦
부드러운 곡선 형태
◦
모든 시간에서 값이 존재
◦
값의 변화가 연속적
◦
자연계의 실제 소리 형태
•
이산 신호(Discrete Signal)
◦
디지털 신호(아날로그 신호를 디지털 변환 후의 형태)
◦
일정 간격으로 샘플링된 값들의 집합
◦
유한한 정밀도를 가짐
◦
계단식 형태
◦
일정 간격으로 샘플링된 지점에서만 값이 존재
◦
정해진 크기 단계로만 값을 표현
◦
컴퓨터로 처리 가능한 형태
디지털 신호 처리•
아날로그 신호(예: 음악이나 음성)를 디지털 신호(컴퓨터가 이해할 수 있는 형태)로 변환
◦
정의: 연속 신호를 이산 신호로 변환하는 과정
◦
사운드를 처리하기 위해 아날로그 신호를 잘게 쪼개 이산적인 디지털 신호로 표현해야 함
◦
이때 무한히 쪼개서 저장할 수는 없으므로, 기준을 세워 아날로그 정보를 쪼개 대표값을 사용, 이를 샘플링이라 함
◦
주로 사용할 때 시간을 기준으로 아날로그 정보를 쪼개는 Time Domain 방식을 사용
<샘플링과 양자화의 예시>
◦
◦
단위: Hz (Hertz = 초당 횟수)
◦
예를 들어, 44.1 KHz는 1초를 44100 등분해서 오디오 데이터를 추출
(1초 동안 44,100번 샘플링)
◦
sampling rate는 아날로그 정보를 얼마나 잘게 쪼갤지를 결정
◦
잘게 쪼갤수록 정보 손실이 줄어들지만, 데이터의 크기가 늘어남
◦
시간이 길어져도 샘플링 간격은 일정함 (샘플링 레이트에 의해 결정)
◦
시간 단위당 샘플링 횟수를 나타내는 비율
◦
나이퀴스트-샤논 표본화 정리
▪
디지털 신호처리에서 아주 중요한 규칙
▪
디지털 변환을 하기위해 샘플링을 하게 돼 신호의 정보량이 손실됐지만 원래 신호로 복원하고 싶다. 어떻게 최대한 자연스럽게 원래의 신호로 복원할 수 있을까?
▪
최대 주파수의 2배 이상으로 샘플링
▪
아날로그 신호(예: 음악이나 음성)를 디지털 신호(컴퓨터가 이해할 수 있는 형태)로 변환할 때 어떻게 하면 신호를 완벽하게 복원할 수 있는지
▪
신호를 완벽하게 복원하려면 그 신호의 가장 높은 주파수의 두 배보다 높은 주파수로 샘플링(표본화)해야 한다고 해
▪
예를 들어, 우리가 최대 주파수가 20kHz인 음악을 디지털로 변환하려면 최소 40kHz로 샘플링해야 해. 그렇지 않으면 신호가 제대로 복원되지 않아서 왜곡이 생길 수 있어.
▪
인간 가청 주파수(20Hz~20kHz) → 최소 40kHz 필요
•
양자화(Quantization)
◦
샘플링된 값을 디지털 값으로 변환하는 과정
▪
아날로그 신호의 연속적인 값을 이산적인 값으로 변환
▪
예: 1.23456….과 같은 연속적인 값을 1.23과 같이 유한한 숫자로 반올림하는 것
◦
비트 심도(Bit Depth)
▪
디지털 오디오에서 소리의 크기를 얼마나 세밀하게 표현할 수 있는지를 나타내는 단위
▪
16비트: 65,536개(-32,768 ~ +32,767)의 레벨(단계)로 소리의 크기를 표현 (CD 음질)
▪
24비트: 약 1,677만개의 레벨(단계)로 더 섬세하게 소리 표현 가능(전문 음향 작업)
◦
양자화 오차(Quantization Error)
▪
아날로그 신호를 디지털로 변환할 때 발생하는 오차를 의미
▪
반올림/반내림으로 인한 오차
•
예: 3.7이라는 값을 4로 반올림하면 0.3의 오차가 발생하는 것과 같은 원리
•
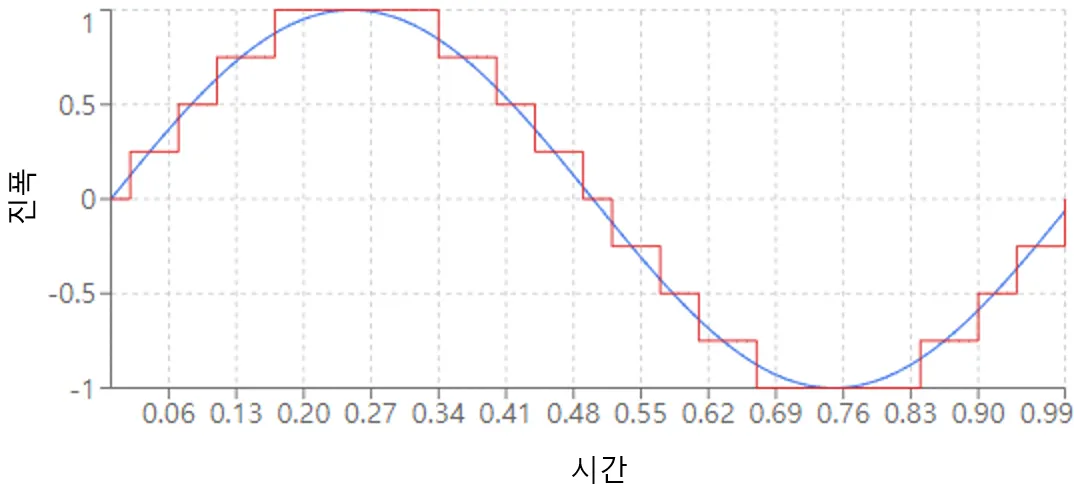
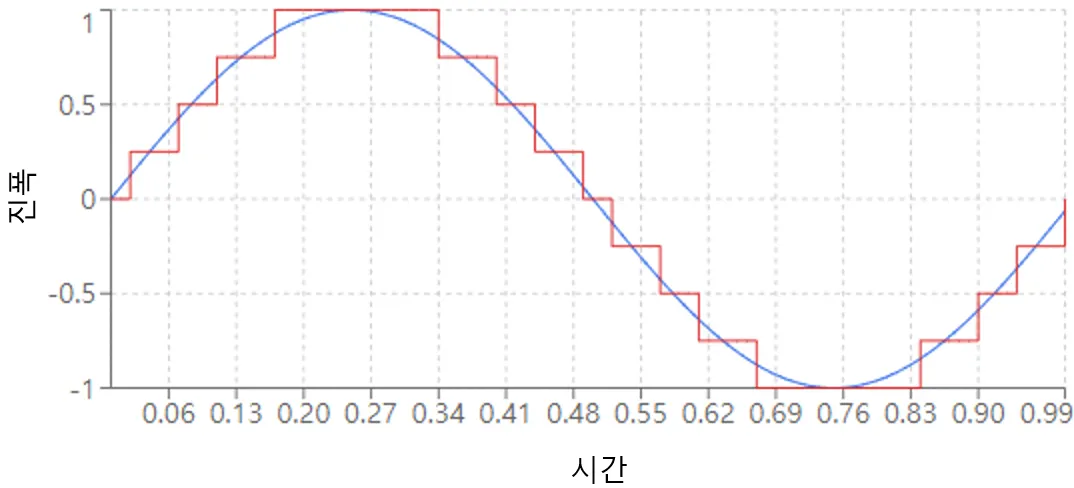
마치 계단식으로 끊어지는 것처럼 표현되어 원본 소리와 차이가 생김
<샘플링과 양자화의 예시>
▪
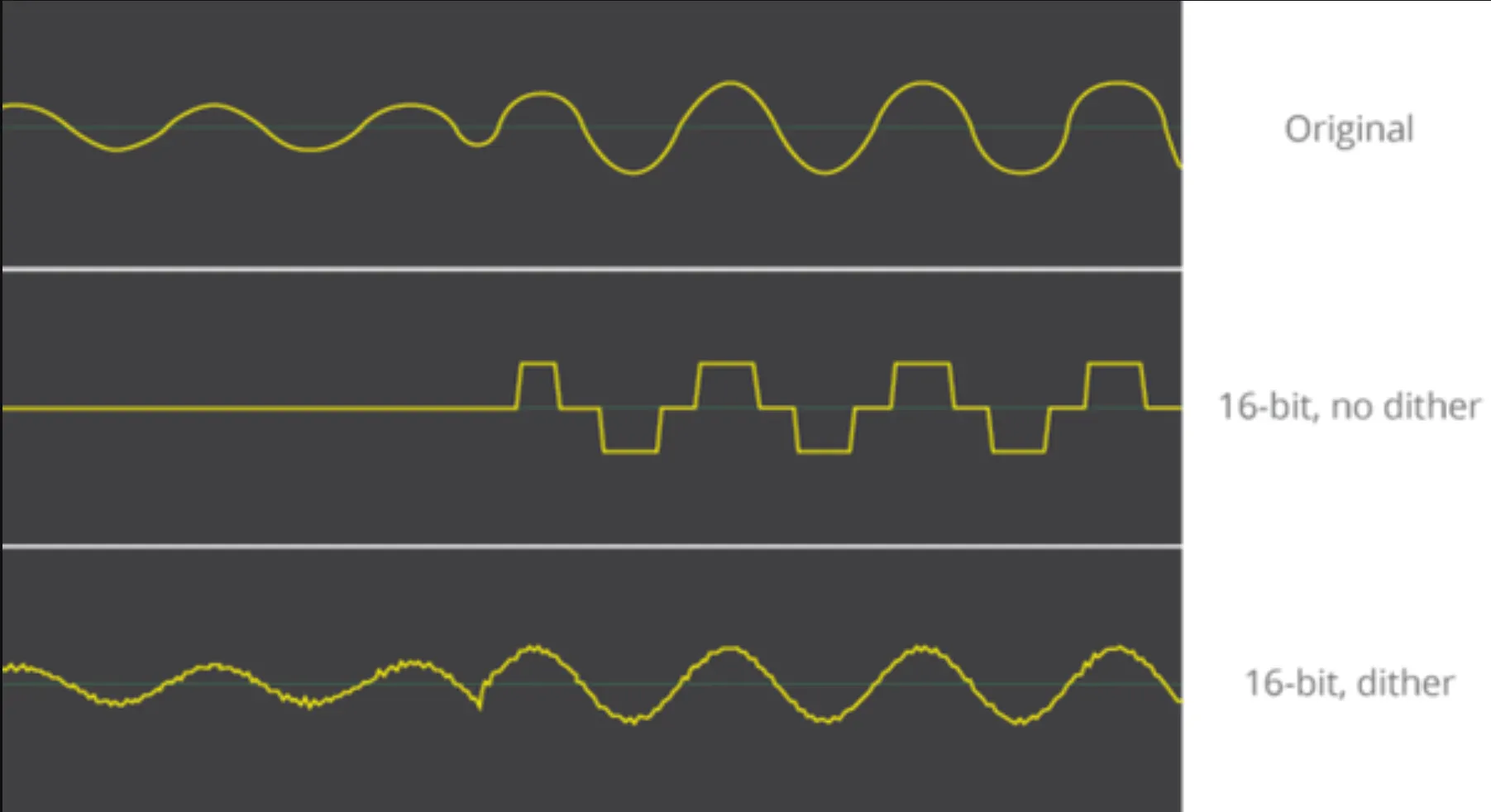
디더링(Dithering)으로 개선 가능
•
양자화 오차를 줄이기 위해 의도적으로 작은 노이즈를 추가하는 기술
•
마치 흐릿한 그라데이션 효과를 주는 것처럼 거친 단계를 부드럽게 만듦
•
특히 작은 소리를 디지털로 변환할 때 유용
•
꼭 디더링이 단순 양자화보다 더 좋은 것은 아님
2. 동작 원리
사인 함수(sine function)
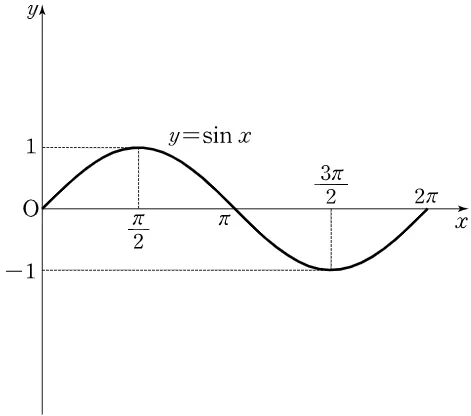
<사인 함수의 그래프: >
•
음압의 변화를 나타내는 시계열 데이터 중 가장 단순한 형태가 사인 함수임
◦
다양한 소리나 신호의 복잡한 구조를 표현하기 위해 사인 함수 외 다른 파형이 사용될 수 있음
다른 파형의 예시
•
사인파는 소리, 빛, 전기 신호 등 다양한 주기적 현상을 가장 단순하게 나타낼 수 있는 기본 단위
•
푸리에 정리 이론에 따르면, 모든 주기적인 신호는 여러 사인파의 합으로 표현될 수 있음
음성 처리에서의 사인파의 구성 요소•
진폭(Amplitude)
◦
진동의 세기(위 아래로 움직이는 폭)
◦
소리의 크기로 인식됨
•
주파수(Frequency) or
◦
진동의 속도
◦
주파수가 높으면 빠르게 진동함
◦
소리의 높낮이로 인식됨
◦
는 헤르츠(Hz)로 나타내며, 신호가 1초 동안 몇 번 진동(반복)하는 지를 나타냄
(1 Hz는 1초에 한 번 진동한다는 뜻, 1초에 50번 진동하면 주파수는 50 Hz)
◦
(오메가)는 로 계산되며 각속도라고도 함 ()
(가 0에서까지 변할 때 값이 한 사이클)
(수학적 계산(미분, 적분)이 더 편리하여 사용하며, 1초에 몇 라디안(각도)인지 파악하는 것)
.gif&blockId=27aae57f-e3a1-4496-ad30-8cda90abf665)
<주파수: sin(빨간색), cos(파란색)> <선형 변환> <라디안>
•
위상(Phase)
◦
사인 함수의 시작 시점
◦
소리의 시간 차이
◦
위상 만큼 출발이 늦어짐 → 위상의 차이는 소리의 시간차로 인식됨
음성 처리에서의 사인 함수의 수식
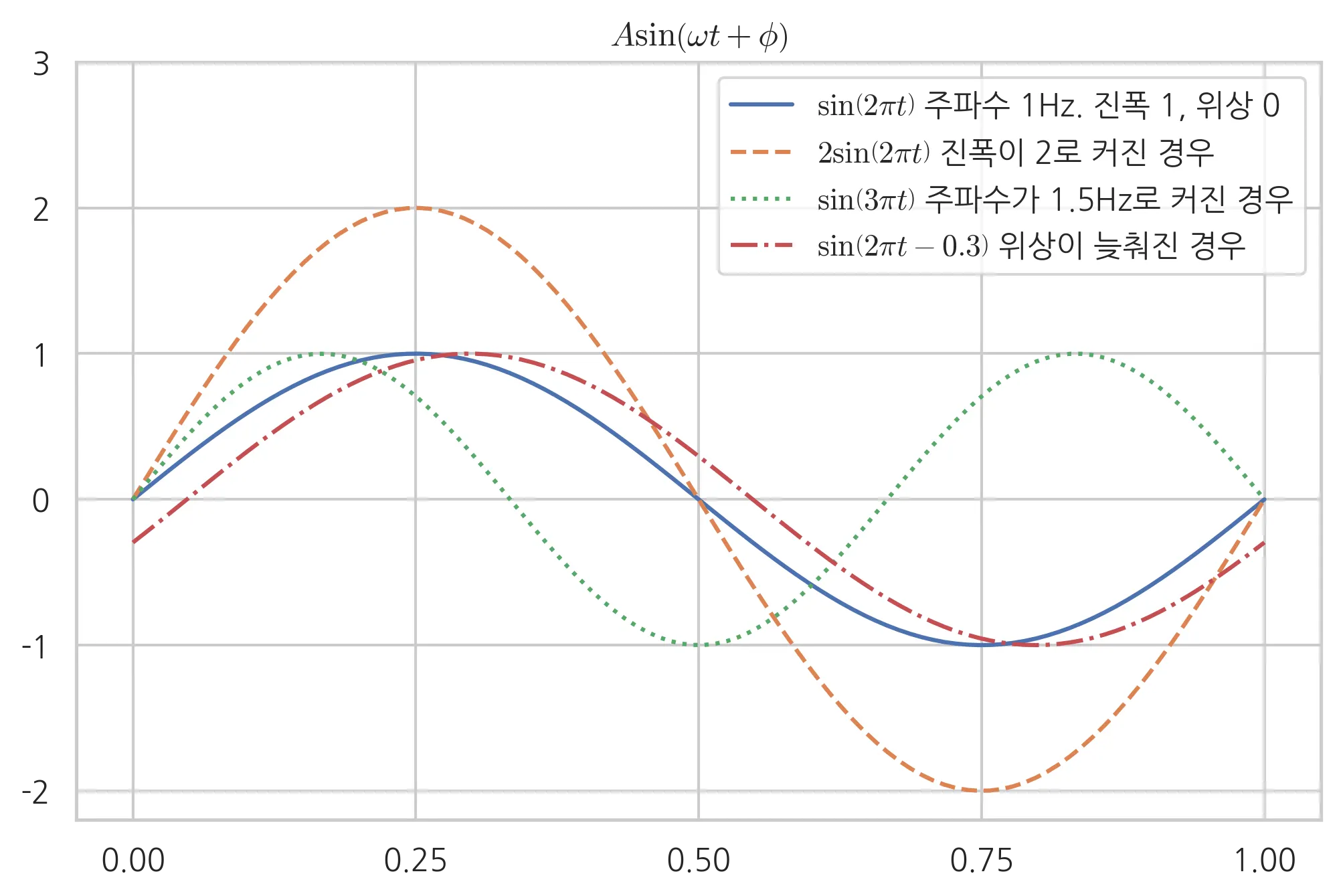
<여러가지 사인 함수를 보여주는 그래프>
•
또는
◦
여기서 는 시간을 나타내며 보통은 초(second) 단위임
•
축 시간 대입
◦
음성신호를 사인함수로 표현할 때는 축에 시간 를 넣음
◦
음성은 시간에 따라 변하는 신호이기 때문 (t가 시간을 나타내어 소리의 변화를 표현 가능)
◦
→
•
진폭 추가
◦
기본 함수: 확장된 함수:
◦
진폭 () : 값의 범위를 에서로 확장함
◦
가 커지면 파형의 높이도 커짐
•
주파수 추가
◦
확장된 함수:
◦
주파수 () : 주파수 를 추가하면, 함수의 주기(반복 주기)가 변화함
◦
가 커지면 파형이 더 자주 반복됨(주기가 짧아짐)
◦
는 시간 변수()에 곱해져서 주기를 조절
•
위상 추가
◦
확장된 함수:
◦
위상 (): 위상 를 추가하면, 파형의 시작 지점이 이동함
◦
가 0이 아닌 값이면 파형이 축을 기준으로 좌우로 이동함
(추가)
코사인 함수는 사인 함수와 위상이 90도 라디안 차이가 있어 사인 함수의 일종으로 볼 수 있음
주기와 주파수의 관계•
주파수()와 주기()는 서로 역수 관계임
◦
주파수(): 1초 동안 몇 번 진동하는지
예: 2 Hz = 1초에 2번 진동
◦
주기(): 1번 진동하는데 걸리는 시간 ()
예: 가 2 Hz면 = 1/2초 = 0.5초 (한번 진동하는데 0.5초 걸림)
•
주파수가 높을수록 주기는 짧아지고, 주파수가 낮을수록 주기는 길어짐
•
or
•
따라서 사인 함수는 아래 식처럼 작성가능
싱글 톤•
주파수는 사람에게 음의 높이(tone)으로 인식됨
◦
주파수가 높을수록 높은 음(고음)
◦
주파수가 낮을수록 낮은 음(저음)
•
싱글톤이란 하나의 주파수만 사용하는 순수한 소리임
◦
기계음 “삐-” 와 같은 소리
◦
피아노 소리나 사람의 목소리는 여러 주파수가 섞여있어 싱글 톤이 아님
◦
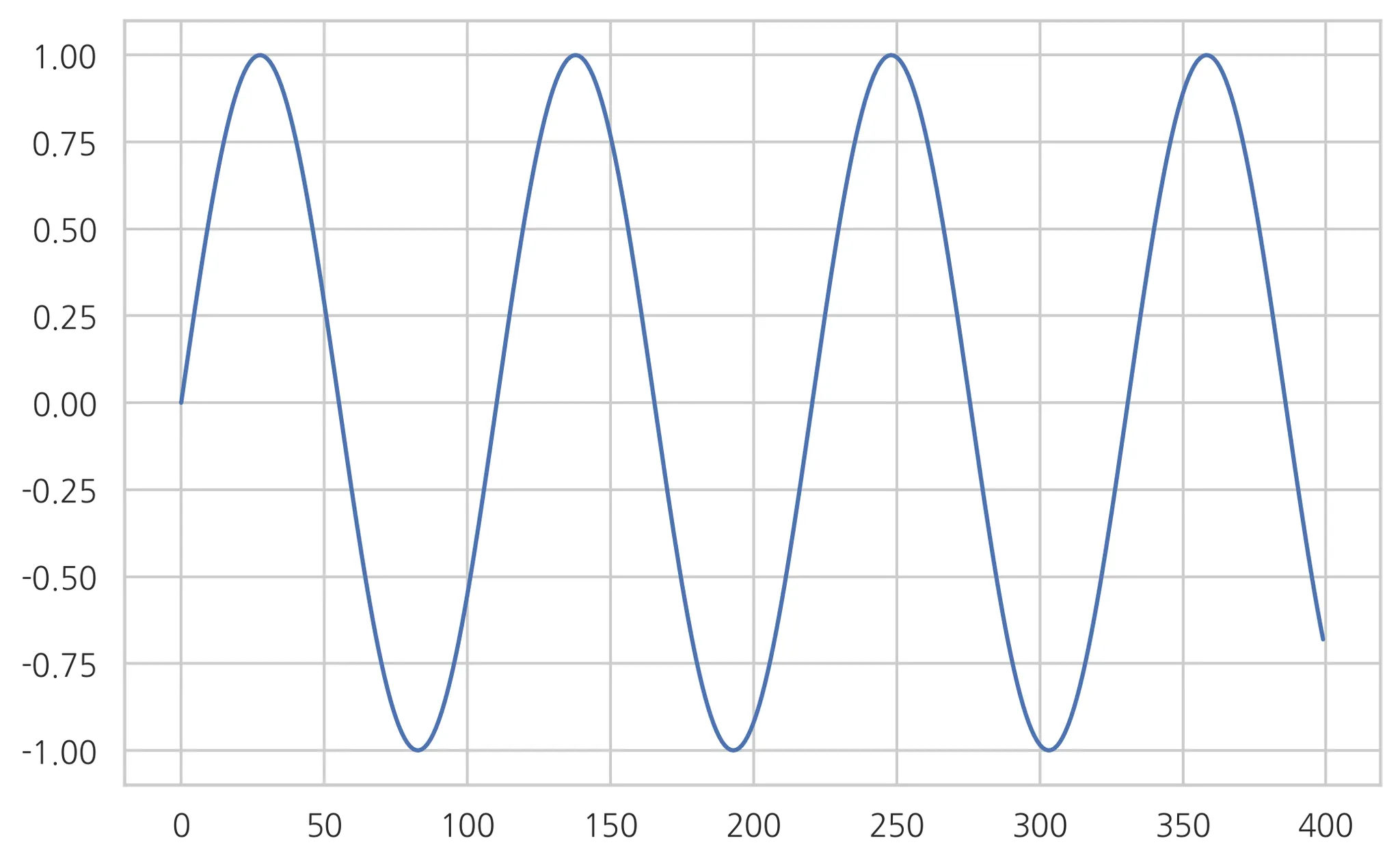
예: 전화 통화연결음에서 “뚜- 뚜-” 하는 소리 400~450 Hz의 단일 주파수 사용
<400 Hz 단일 주파수>
•
음계에서 기준이 되는 가온다(middle C)음은 261.62 Hz의 싱글 톤임
◦
반음(semitone, half tone, half step)이 올라갈 때마다 배만큼 주파수가 높아짐
◦
1옥타브(octave, 12반음)가 올라가면 주파수는 2배가 됨
◦
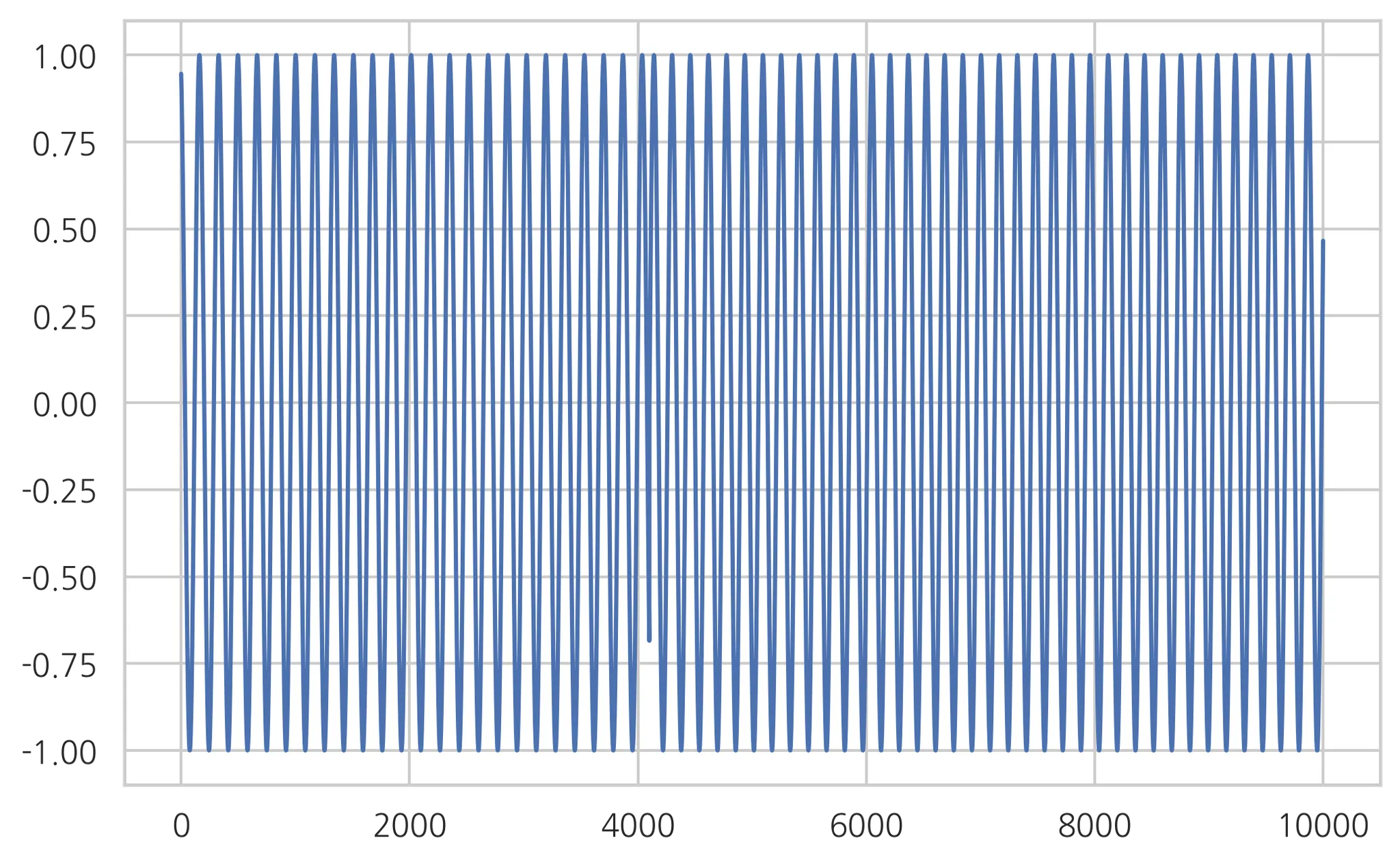
아래 소리는 가온다로부터 한 옥타브(12반음)가 올라가는 소리임
•
복수의 싱글톤을 더하여 한번에 소리를 내면 화음이 됨
◦
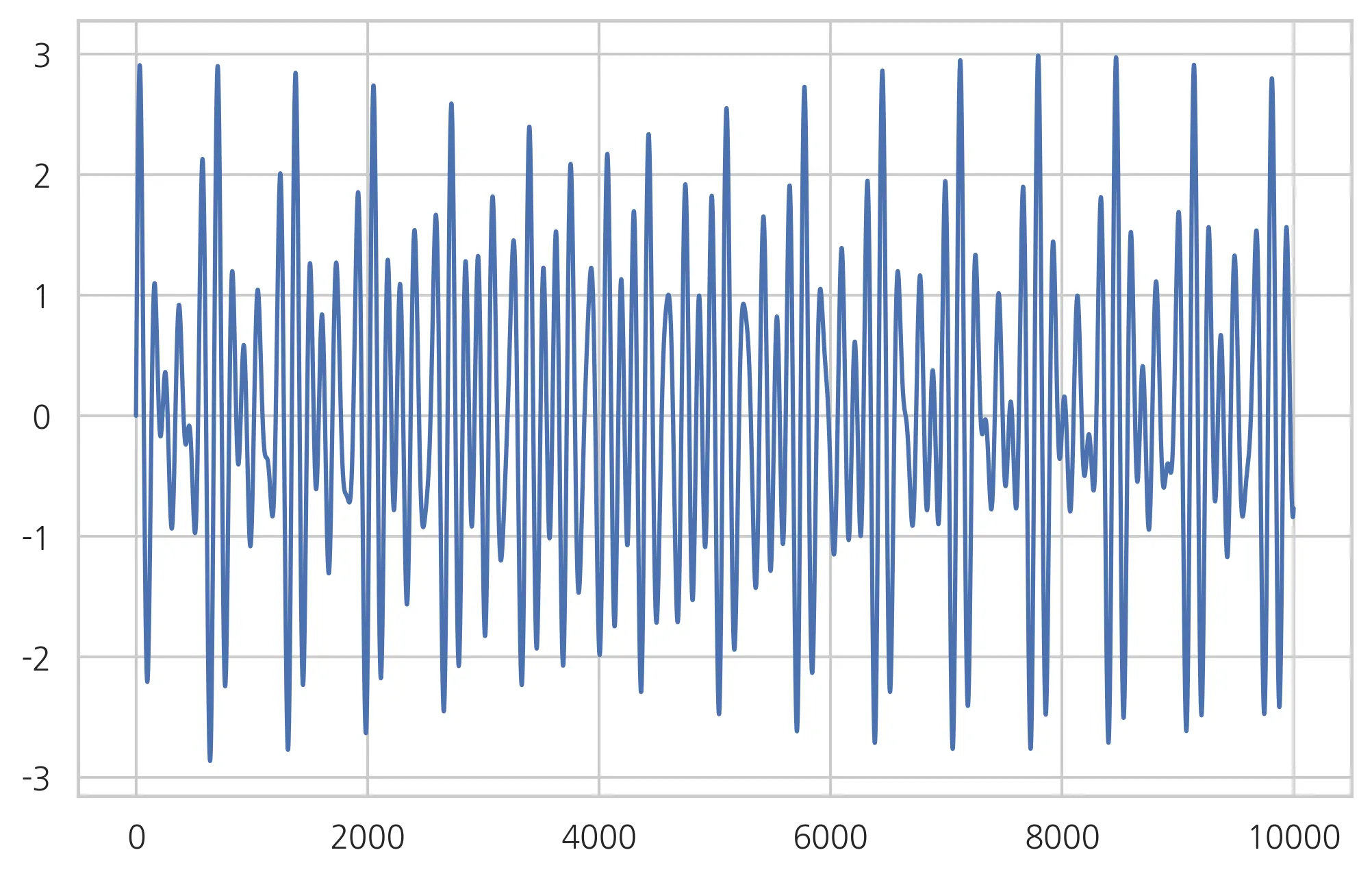
예: 도(C) 미(E) 솔(G) 3도 화음은 아래 소리와 같음
<도(C) 미(E) 솔(G) 3도 화음>
wave 형식 파일•
wave 파일은 음압 시계열 데이터를 저장하는 가장 기본적인 파일 형식임
◦
.wav 확장자로 표시
◦
보통 초당 44100번 음압을 측정하고 ~ 까지의 2바이트(bytes) 숫자로 기록함
Dual-tone multi-frequency(DTMF) signaling
