3.1 시계열 사용되는 자료 분석
•
일반적 데이터 응용 기법
◦
히스토그램
데이터의 분포를 시각화하여서 데이터의 중심 경향과 분산을 확인
◦
도표 그리기
시계열 데이터를 선 그래프, 산점도, 막대 그래프 등의 다양한 도표로 시각화하여 데이터의 패턴을 확인
◦
그룹화 연산
데이터를 그룹으로 나누어 각 그룹에 대한 특성을 비교하고 분석
(예; 특정 기간에 대한 데이터를 그룹으로 나누어 각 그룹의 평을 비교하는 등의 분석을 수행)
•
시간 기법
◦
데이터가 서로 시간 관계가 있는 상황에서 의미 있음
3.1 친숙한 방법
시계열 데이터와 비시계열 데이터에 적용하는 과정 탐색은 동일함
•
새로운 데이터를 다룰 때 기존의 질문
1.
긴밀한 상관관계를 가지는 열이 있나요?
2.
관심 대상 변수의 전체 평균과 분산은 무엇인가요?
⇒ 도표 그리기, 요약 통계 내기, 히스토그램 적용, 산점도 사용으로 해결 가능
•
시간 고려한 질문
1.
분석값의 범위가 무엇인지?
2.
다른 논리적 단위나 기간에 따라 값이 달라지는가?
3.
데이터가 일관성을 갖고 균등하게 측정 되었는가?
4.
아니면 시간이 흐르면서 측정이나 동작 방식에 변화가 있었는가?
⇒ 히스토그램이나 산점도, 요약통계 + 시간축 고려
<그룹화 연산>
3.1.1 도표 그리기
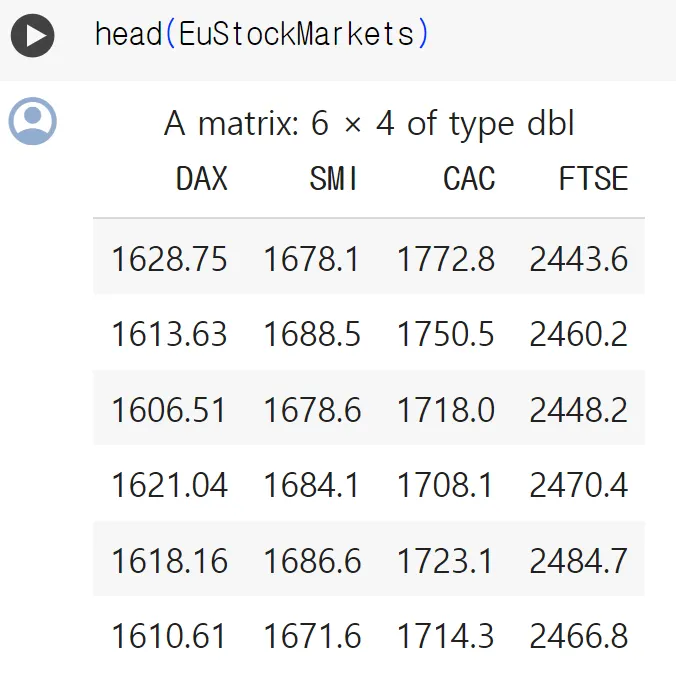
R이 제공하는 EuStockMarkets 시계열 데이터셋(입회일business day만 포함)
•
head ()함수
◦
데이터 프레임이나 배열의 처음 몇 개의 행을 반환하는 함수
◦
기본적으로 처음 6개의 행을 반환(사용자가 원하는 개수를 지정할 수도)
head 함수
•
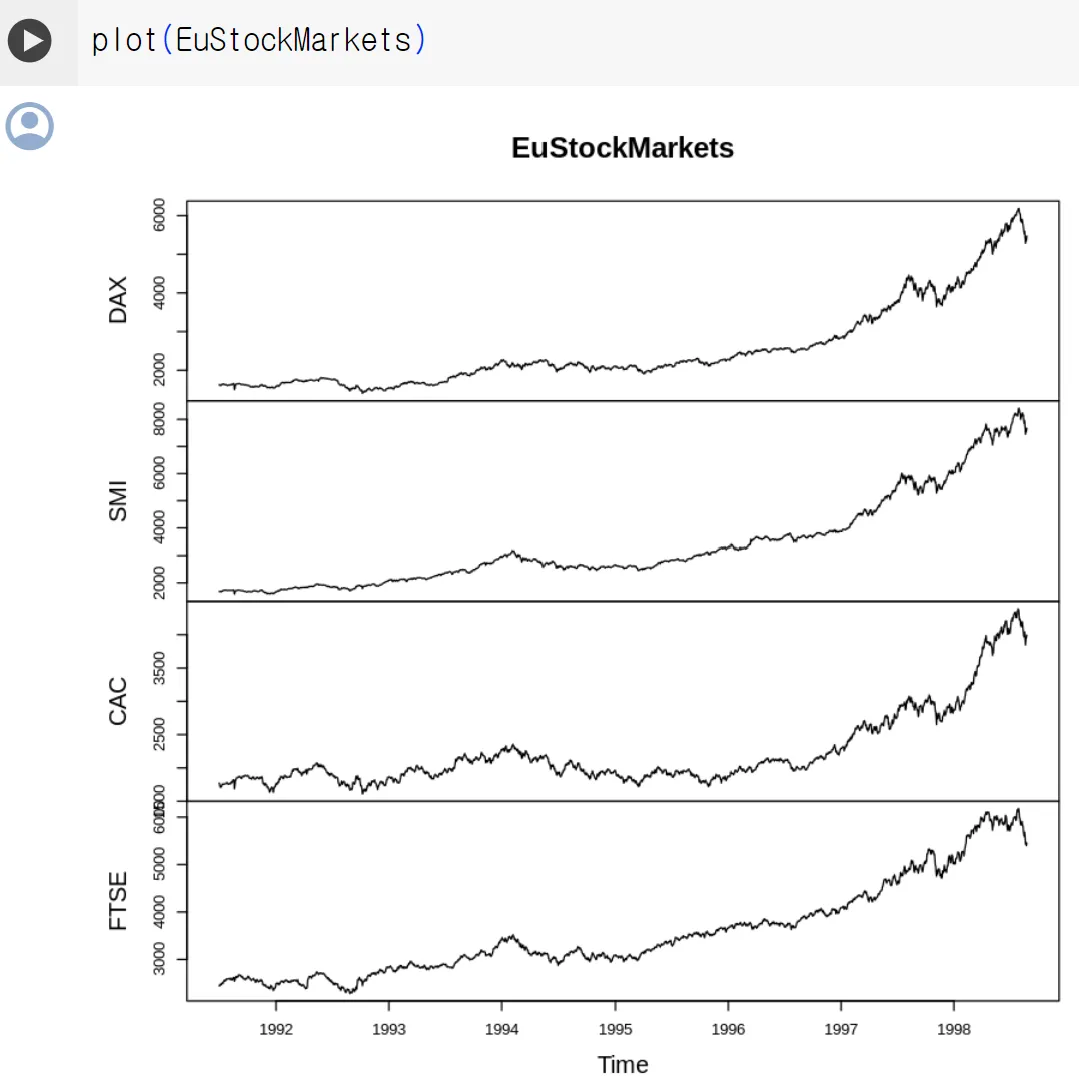
plot() 함수
◦
데이터를 서로 다른 시계열 그래프로 자동 분할할 수 있음
mts 객체 사용(다양한 시계열 동시에 다룸/ 단일 시계열 ts 객체 사용)
plot 함수
•
class함수
◦
R 객체의 클래스(class)를 반환하는 함수
•
frequency 함수
◦
데이터의 연간 빈도를 알아냄
•
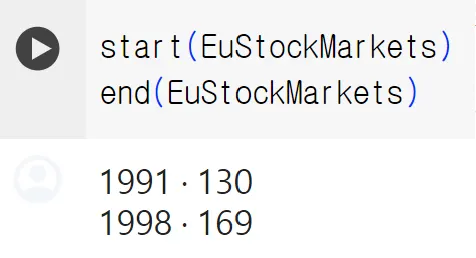
start와 end함수
◦
일련의 데이터에서 처음과 마지막을 알아냄
frequency 함수
class 함수
start 와 end 함수
•
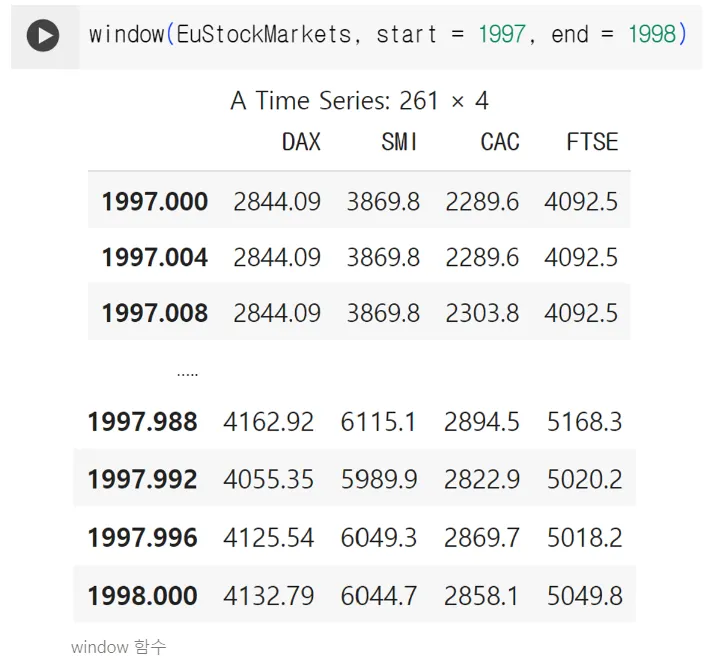
window 함수
◦
데이터에서 시간의 한 부분 범위를 얻을 수 있음
3.1.2 히스토그램
•
히스토그램(Histogram)
◦
도수분포표를 그래프로 나타낸 것
◦
가로축 : 계급
◦
세로축 : 도수(횟수나 개수 등)
•
히스토그램 + 시간축
◦
시간상 인접한 데이터간의 차이를 구할 수 있음
◦
차이에 대한 히스토그램을 측정할 수 있음
◦
예상치 못한 관점에서 데이터를 바라볼 수 있음
•
hist()와 hist(diff())함수
◦
히스토그램 생성 함수, 주어진 데이터 차분을 계산하는 함수
숨기기
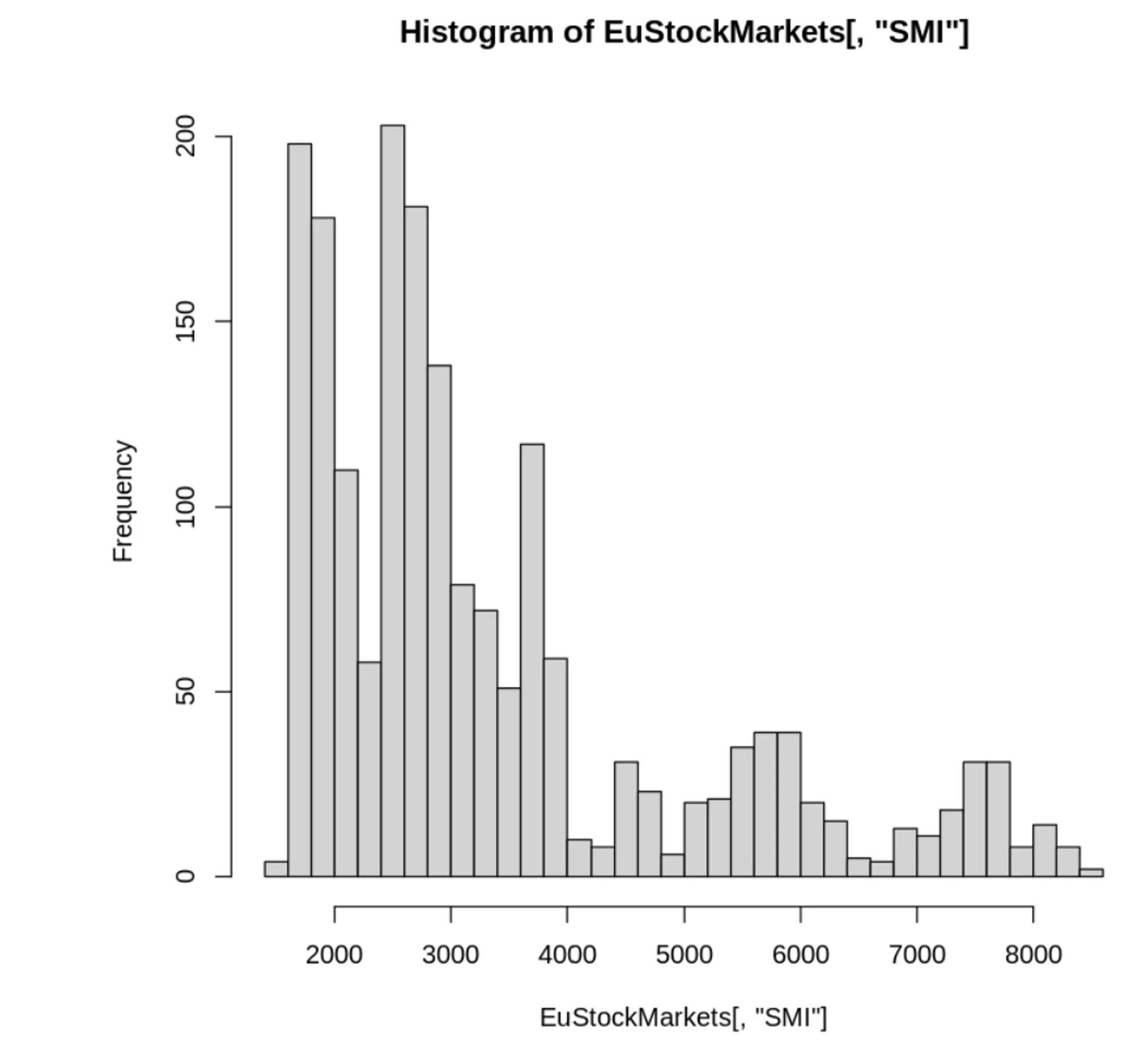
NOT DIFF
데이터의 내제된 추세 반영한 결과
⇒넓게 퍼져 있고 정규분포를 따르지 않음
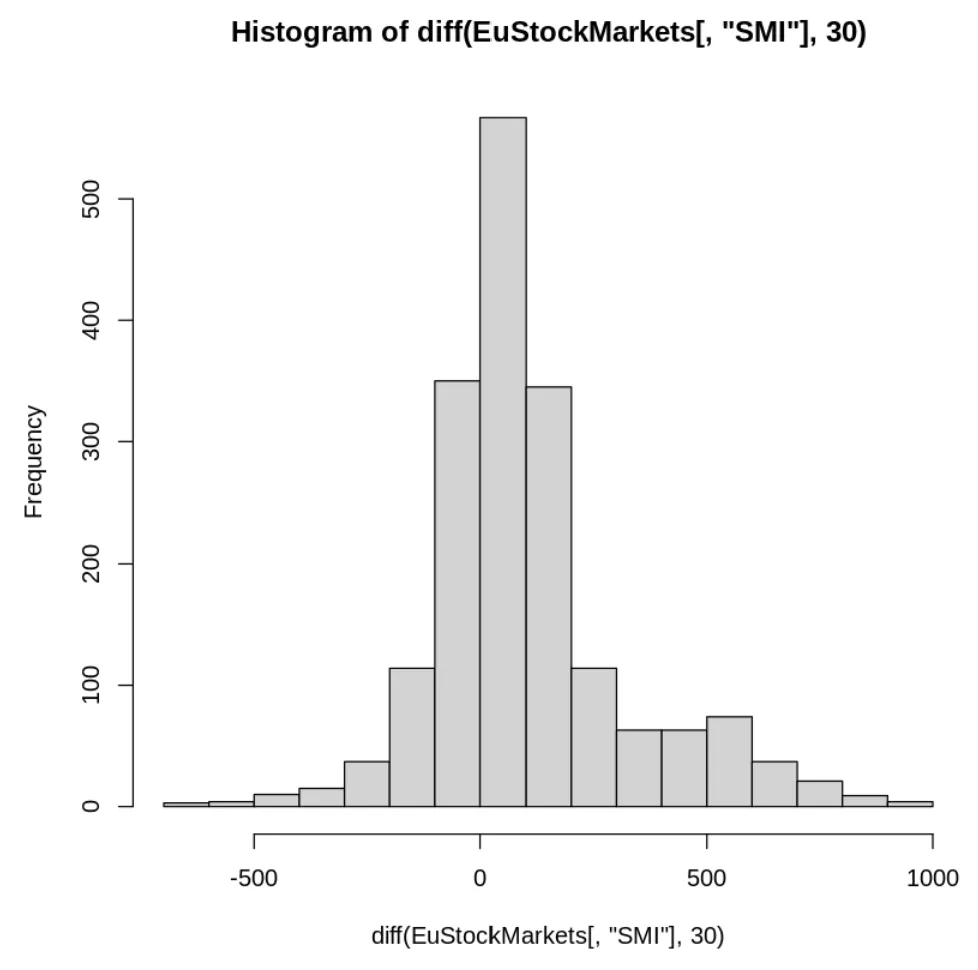
DIFF
추세를 제거하고 시간상 인접데이터 차이를 구함
⇒정규분포를 따르는 형태
•
추세를 제거하기 위해 시간상 인접한 데이터의 차이 구하면, 정규 분포를 따르는 형태로 변화함
•
데이터 샘플링 및 통계 요약을 하거나 질문을 던질 때 시간 규모에 관심을 가져야 함
◦
장기 도표나 차분 히스토그램 시간 규모에 따라 달라짐
3.1.3 산점도
•
산점도(Scatter plot)
◦
비시계열 , 시계열 데이터 모두 유용함
◦
두 변수의 상관관계를 점으로 나타낸것
◦
가로축 : 계급
◦
세로축 : 도수( 횟수나 개수 등)
•
산점도 + 시간축
◦
특정 시간에 대한 두 변수의 관계를 결정할 수 있음
◦
두 변수의 시간에 따른 각각의 변수 값 변동이 갖는 연관성을 결정할 수 있음
▪
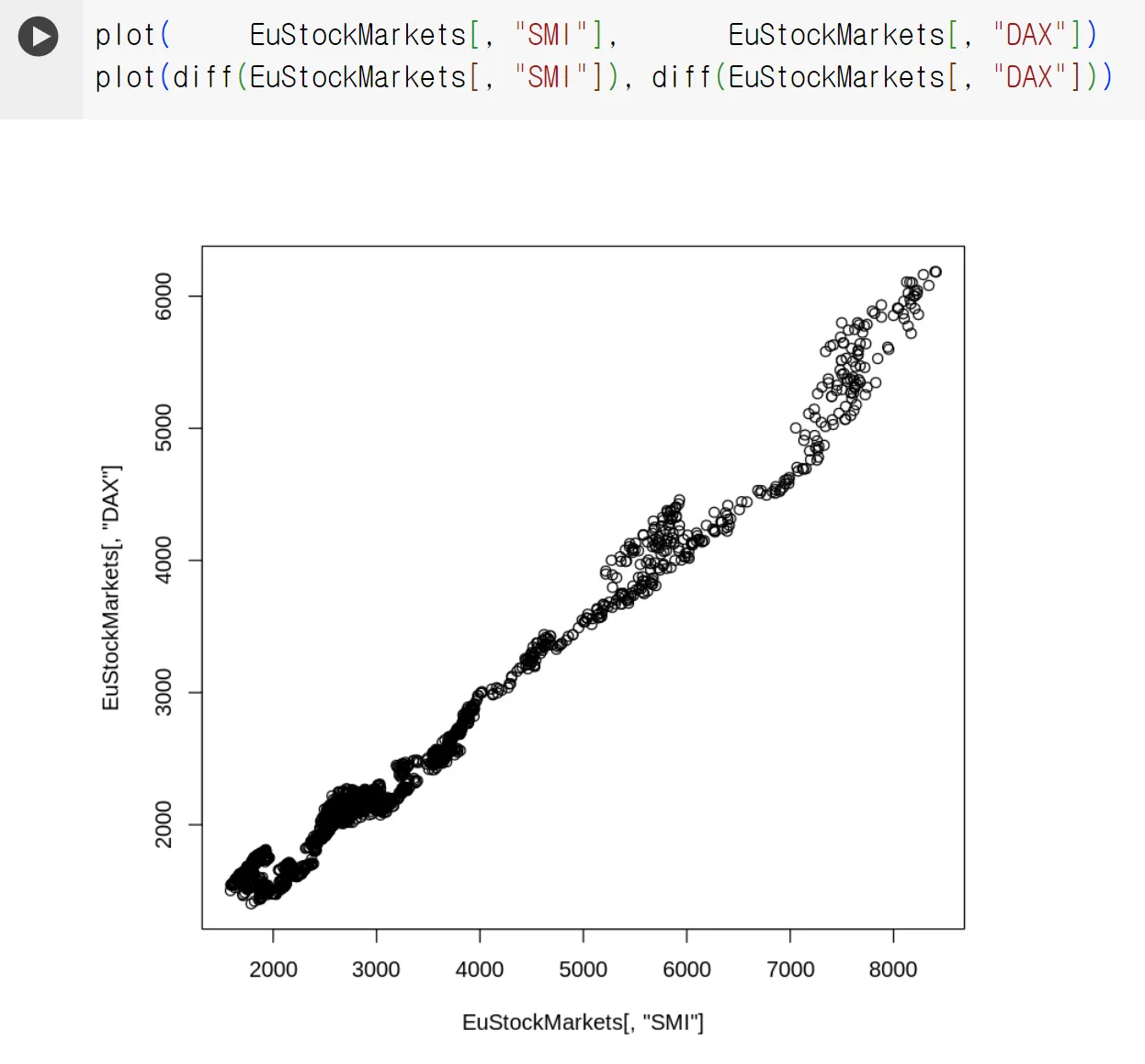
두 주가 지수에 대한 산점도 예시
plot 함수
시간에 따른 서로 다른 두 주식의 가치
매우 강한 상관 관계가 있어 보임
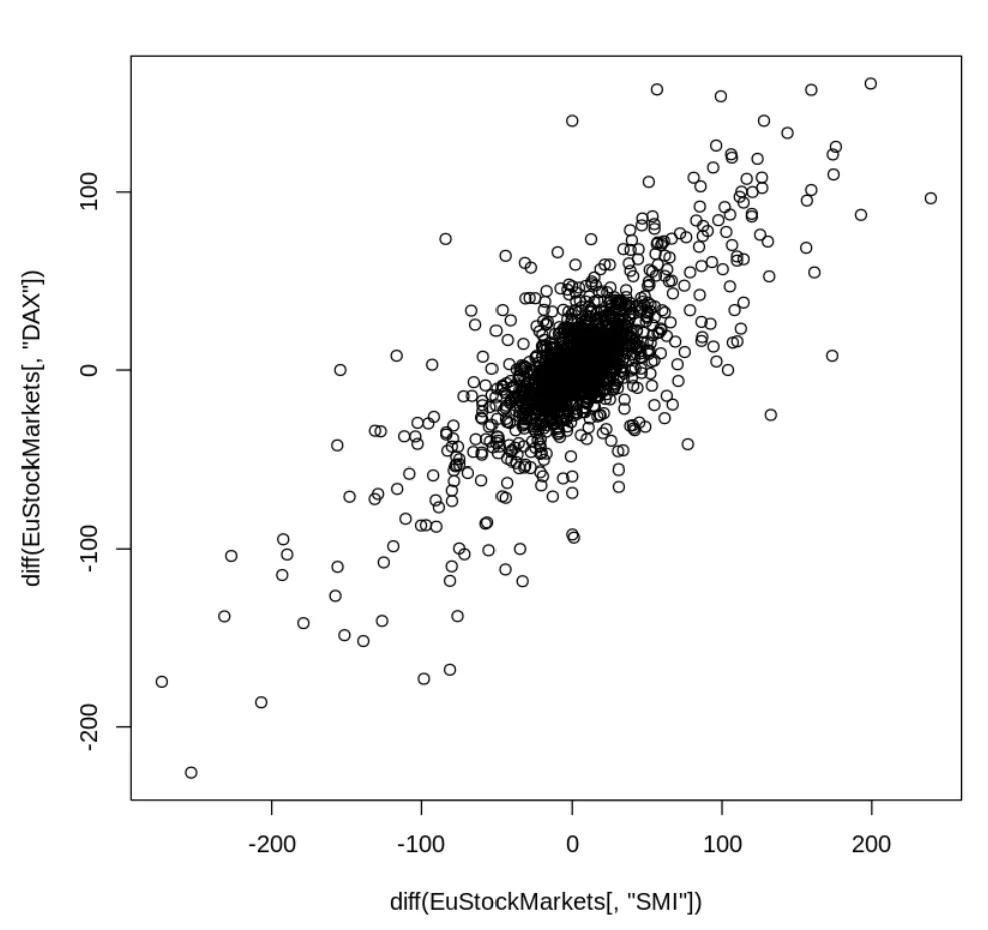
diff() 함수로 구한 두 주식의 일일 가치 변동
실제 보이는 만큼 상관관계가 강하지 않음
•
lag 함수
◦
시간을 미루는 함수
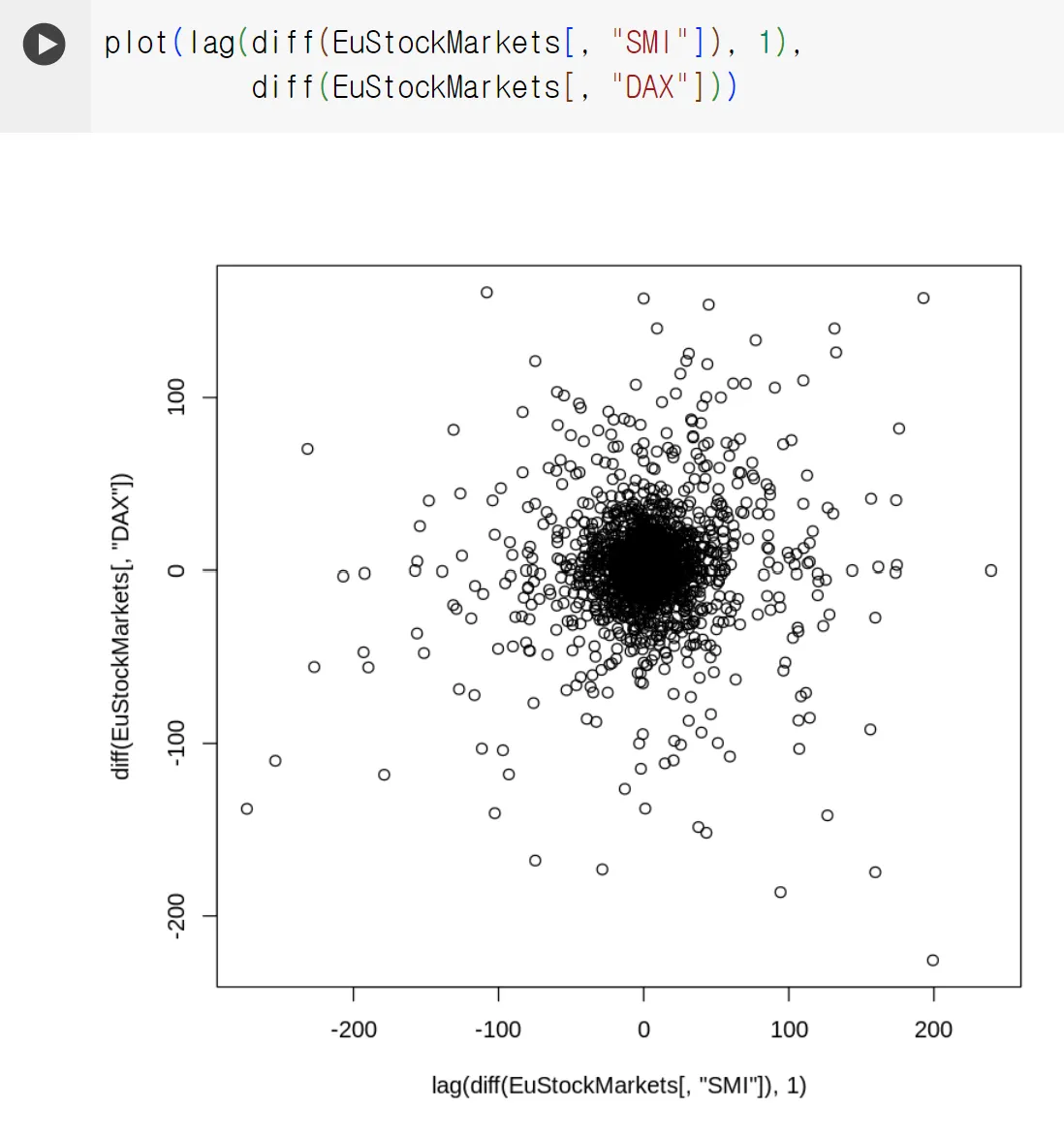
lag 함수를 적용한 산점도
•
시간 상 먼저 알게 된 주가의 변동으로 나중의 다른 주가의 변동을 예측해야 함
◦
산점도 확인하기 전 두 주가 중 하나를 1만큼 시간 상 앞으로 당겨야 함(lag 함수)
◦
두 축의 상관 관계 사라진 것 확인 가능
◦
즉, 한 변수로 다른 변수를 예측하지 못함
•
시간에 따른 변화나 서로 다른 시점의 데이터 사이의 관계가 데이터 동작 방식을 이해하는데 유익한 정보인 경우가 많음
3.2 시계열에 특화된 탐색법
- 시계열 분석시 주요 개념
정상성stationarity
자체상관self correlation
허위상관spurious correlation
위 개념을
•
롤링윈도와 확장 윈도 함수
•
자체상관함수self correlation function
•
자기상관함수autocorrelation function
•
편자기함수partial autocorrelation function 의 기법에 적용함
3.2.1 정상성 이해하기
직관적인 정의
•
정상 시계열에서 측정된 시계열은 시스템의 안정된 상태를 반영함
•
정상 시계열은 시간이 경과해도 안정적인 통계적 속성을 가짐
•
평균, 분산이 시간에 따라 일정
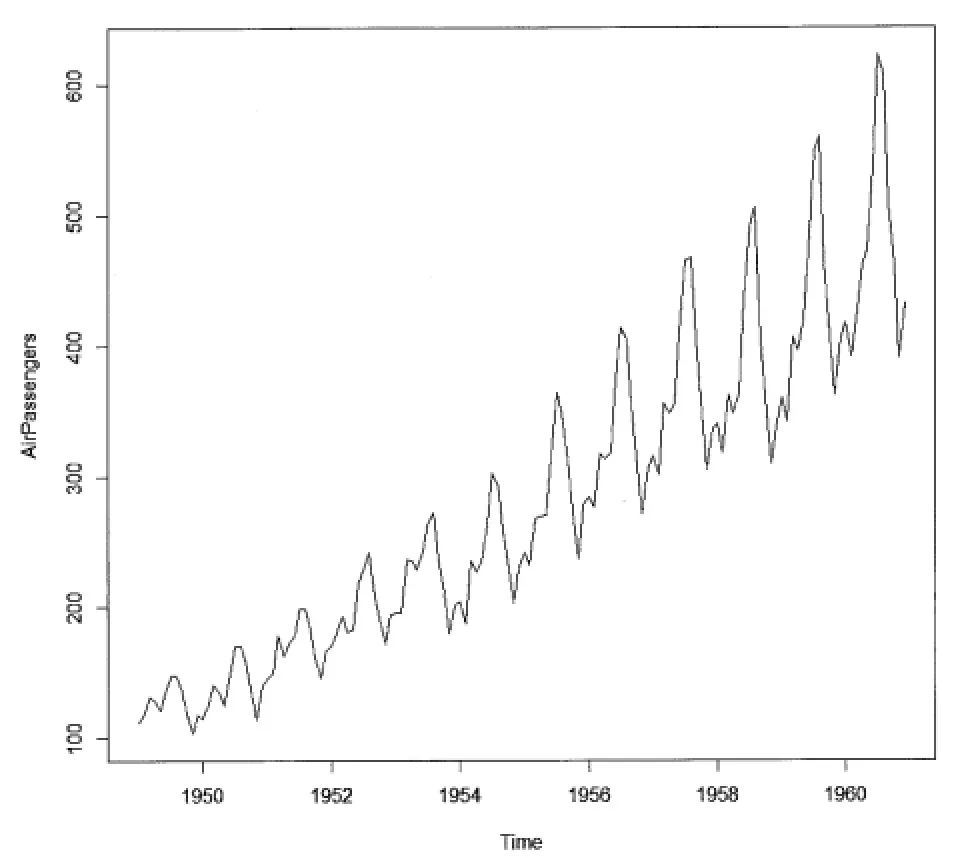
정상이 아님을 보여주는 특징(예:AirPassengers 데이터)
•
평균값이 일정하게 유지되기 보다는 시간에 따라 증가함
•
연간 최고점과 최저점 사이의 간격이 증가하므로 분산이 시간에 따라 증가함
•
강한 계절성이 보임
AirPassengers 데이터셋에 대한 도표
정상성의 정의와 증강된 디키-풀러 검정(augmented Dickey-Fuller Test)
정상 과정 : 모든 시차 k에 대해 의 분포가 t에 의존적이지 않은 것
단위근unit root
확률보행random walk
•
◦
는 현재시간 t의 시계열 값
◦
는 이전 시간 t-1의 값에 곱해지는 변화율
◦
는 이전시간 t-1의 시계열 값
◦
는 현재 시간 t의 무작위 오차항을 나타냄
◦
ϕ=1, 현재시간 값은 이전 시간 값에 변화 없이 무작위한 오차항이 더해진 것으로 나타남
이 경우 시계열 데이터에는 단위근이 존재하게 됨
데이터의 평균 주위로 계속해서 무작위하게 움직이게 되고 시계열 데이터가 추세를 따르지 않고 무작위하게 움직인다는 것을 확인할 수 있음
ADF 검정(augmented Dickey-Fuller Test)
•
디키-풀러 검정
는 시계열 데이터의 차분
ϕ 는 추정된 파라미터 값
ϕ 값이 1인지에 대한 검정은 에서의 파라미터가 0인지에 대한 t-검정으로 볼 수 있음
•
이러한 검정들이 정상성 문제를 완벽히 판별할 수 없음
•
이 검정들은 단위근과 준 단위근을 구분하기 어려움
•
거짓 양성이 발생할 수 있음
•
검정이 특정한 한계점을 가지고 있으며, 모든 종류의 비정상 시계열 문제를 검정하지 않음
<NOTE > 귀무가설의 대안 설정 : KPSS 검정
•
ADF 검정 Augmented Dickey-Fuller Test은 단위근의 귀무가설을 상정함
•
KPSS 검정 Kwiatkowski-Phillips-Schmidt-Shin Test은 정상과정의 귀무가설을 상정함
실전
•
비정상성과 모델 평가
◦
정상성이 아닌 시계열 모델은 시계열의 평가 지표가 달라짐에 따라 정확도가 달라짐
◦
모델의 평균을 추정하는 데 비정상 평균과 분산을 사용하면 시간이 지날 수록 모델의 편향과 오차가 달라지며, 모델의 신뢰도가 저하될 수 있음
•
시계열의 정상화 위한 변환
◦
분산이 변화하는 경우에 로그와 제곱근 사용함
◦
추세는 차분을 구해 제거함(단 3회 이상 차분 계산 시 정상성 문제 해결 힘듦)
•
정규성normality 가정
◦
데이터가 정규 분포를 따른다는 것의 의미
◦
예측 모델링을 위해 사용되는 많은 통계 기법들은 종속 변수가 정규 분포를 따른다고 가정함
박스-콕스Box-Cox 변환은 종속의 변수 분포를 정규 분포에 가깝게 만들기 위해 사용됨
•
변환의 필요성 검토
◦
데이터 변환 전 원본 데이터 간의 거리와 패턴을 고려
◦
변환 후에도 중요 정보가 유지되는지 검토
3.2.2 윈도우 함수 적용
•
롤링 윈도
◦
시계열에 일반적으로 특화되어 사용되는 함수
◦
데이터 압축하거나 평활화하기 위해 사용되며 데이터를 취합함
◦
시계열 데이터의 특징을 잘 이해하고 시각화함
•
R의 filter() 함수
◦
주어진 시계열 데이터에 대해 주어진 필터(가중치)를 적용하여 필터링 된 결과를 반환
◦
이동 평균 및 계열의 선형함수와 관련된 다른 계산을 할 수 있음
## rnorm 함수로 정규분포를 따르는 난수를 100개 추출합니다
x <- rnorm(n=100, mean=0, sd=10) + 1:100
## rep 함수로 1/n 값을 n번 반복하는 배열을 만드는 함수를 만듭니다
## mn에 rep함수를 지정
mn <- function(n) rep(1/n, n)
plot(x, type = 'l', lwd = 1)
## 기본 R의 filter 함수로 롤링 평균을 계산합니다. 각각 5개, 50개 단위로 롤링 합니다
## mn(5) : 윈도우 수가 5개 간격으로 평균계산
## mn(50) : 윈도우 수가 50개 간격으로 평균 계산
## lty = 2 : 빨강 , lty = 3 : 녹색
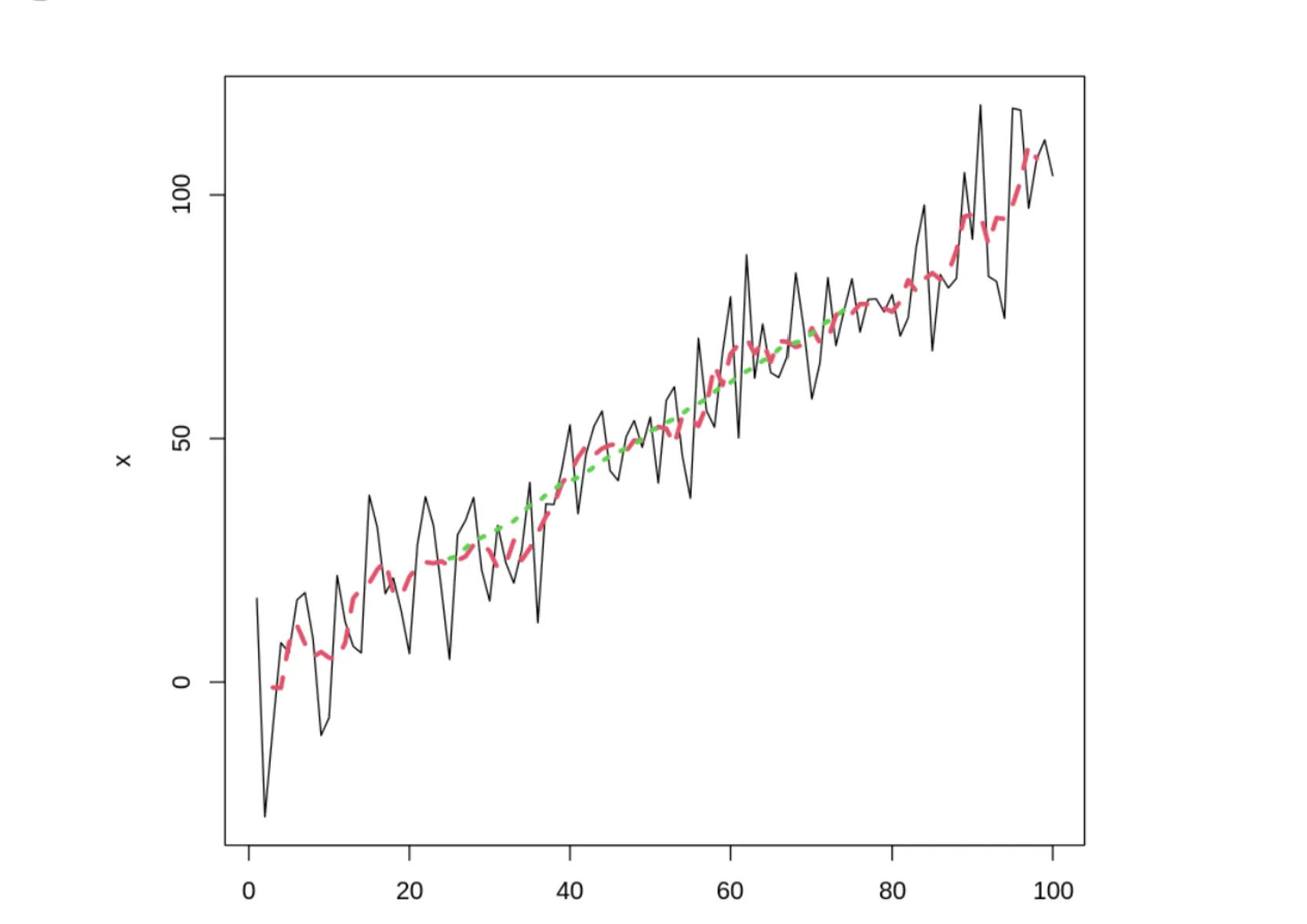
lines(filter(x, mn( 5)), col = 2, lwd = 3, lty = 2)
lines(filter(x, mn(50)), col = 3, lwd = 3, lty = 3)
R
복사
롤링 평균 평활화로 탐색적 곡선 두개를 만듬
•
이 곡선 이용하여 노이즈가 많은 데이터의 추세를 찾음
•
선형동작의 어떤 종류의 편차가 단순한 노이즈인지 조사해볼 수 있음
•
filter함수는 일차변환에 기반하므로 일차결합하지 않은 함수에서는 사용할 수 없음
•
zoo 패키지의 rollapply함수를 사용하는 것이 유용함
## 기능을 좀 더 '사용자 정의'하여 사용할 수도 있습니다.
install.packages("zoo")
require(zoo)
## x를 zoo 객체로 만들어 각 데이터를 인덱싱 해 줍니다
## rollapply 함수는 데이터, 윈도우크기, 적용함수, 롤링적용 정렬 방향,
## 윈도우크기만큼 데이터가 없어도 적용할 것인가? 등의 인자 값을 지정합니다
## rollapply 함수는 이동평균이나 합계(sum()) 함수같은 연속연산이 가능
## align left 미래에서 과거 방향으로 이동 평균 / align right는 과거에서 미래 방향으로 이동평균
## 미래데이터를 사용할때는 사전관찰 문제가 발생할 수 있음
## partial = True 윈도우가 20일때, 널값이 있어 19개의 데이터포인트만 있어도 계산한다
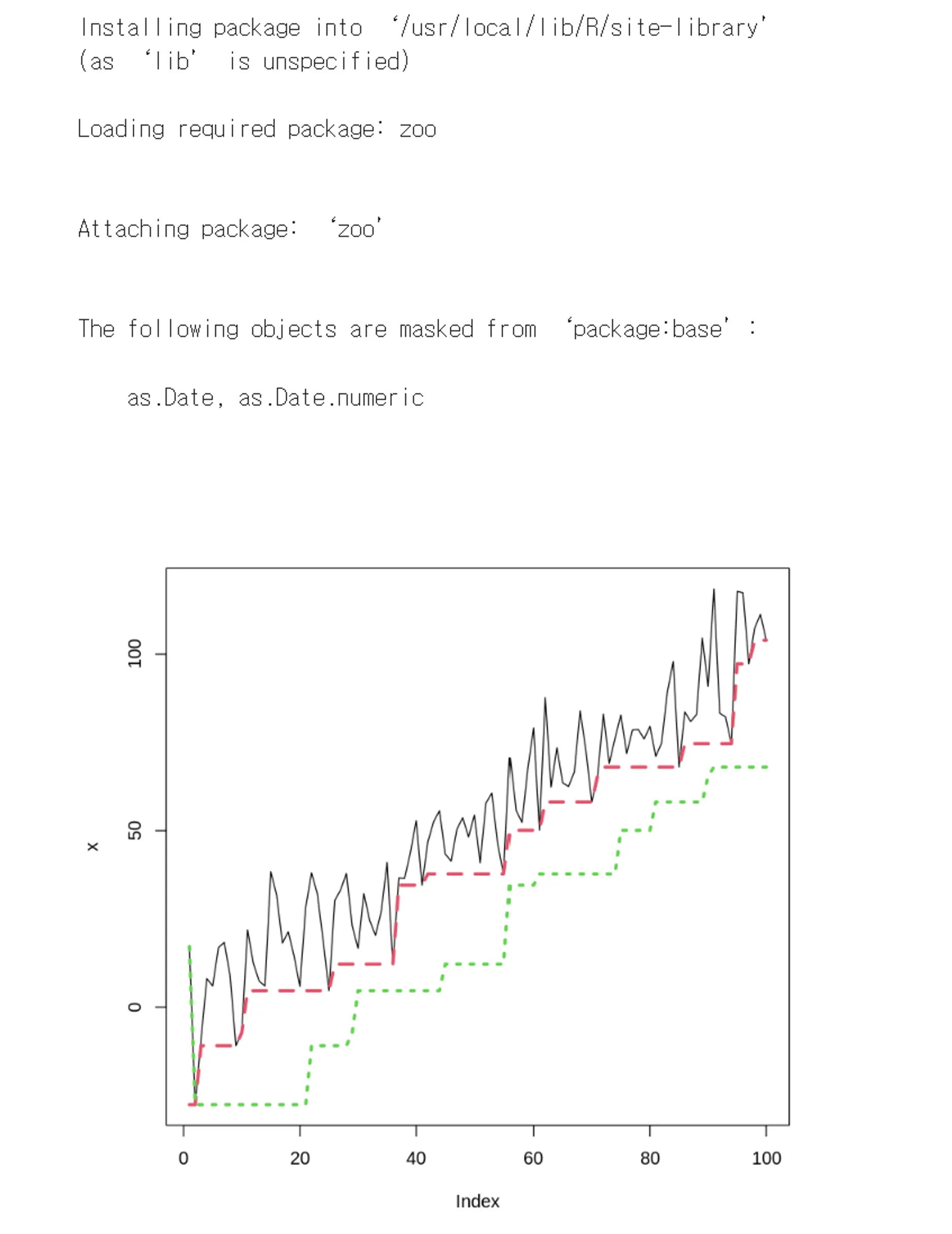
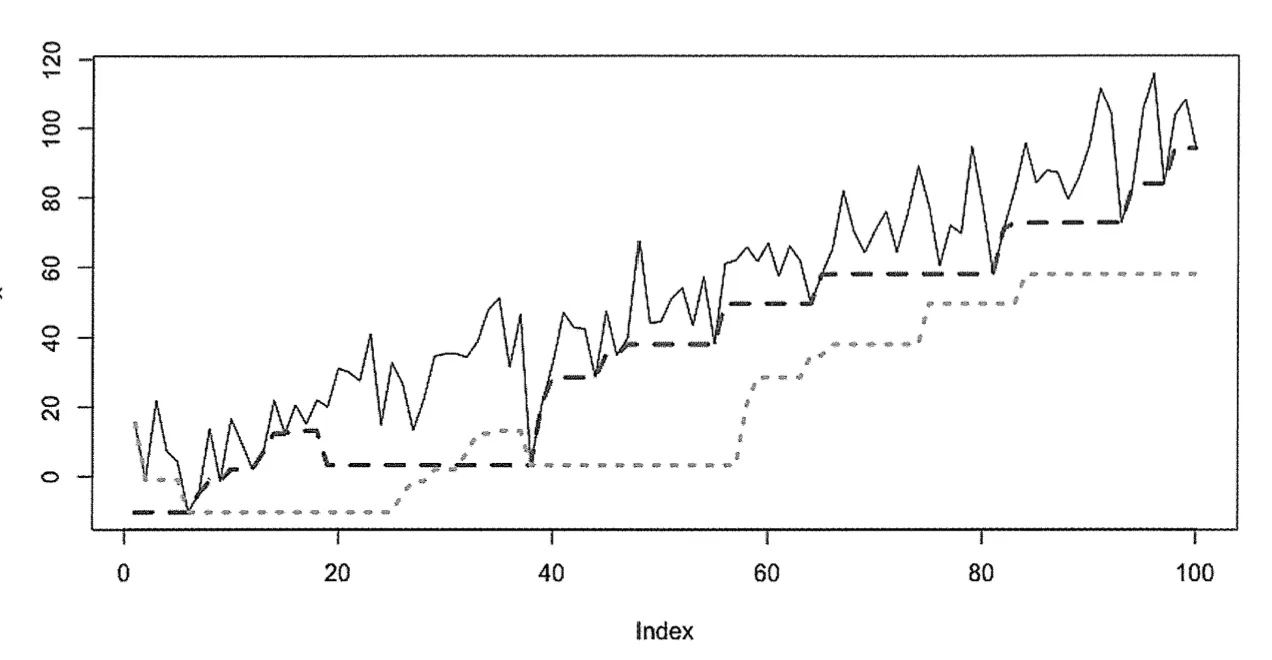
f1 <- rollapply(zoo(x), 20, function(w) min(w),
align = "left", partial = TRUE)
f2 <- rollapply(zoo(x), 20, function(w) min(w),
align = "right", partial = TRUE)
plot(x, lwd=1, type='l')
lines(f1, col=2, lwd=3, lty=2)
lines(f2, col=3, lwd=3, lty=3)
R
복사
<시계열을 위한 R의 다양한 옵션>
•
ts 객체
◦
균등한 간격의 완전한 시계열을 가정
◦
시계열의 시작, 끝, 빈도만을 저장함
◦
연도와 월같이 반복되는 주기 지원
•
zoo 객체
◦
타임스탬프를 색인 속성으로 저장(균등한 주기적인 시계열을 요구하지 않음)
◦
수직이나 수평으로 출력
◦
벡터나 행렬
확장 윈도expanding window
•
시계열 분석에서 사용되는 윈도(window) 기법중 하나
•
롤링윈도rolling window와 달리, 일정한 크기의 윈도를 유지하는 대신 데이터를 확장하여 시계열 전체 데이터를 포함할 때까지 윈도를 확장함
•
안정적인 요약통계를 추정시 의미있음
•
시간에 따른 검정 통계량test statistic의 추정치 확실
•
시스템이 정상일 때 가장 잘 동작함
•
더 많은 정보 수집:실시간으로 요약통계를 추정할 때, 온라인online 상태로 유지하는데 유용함
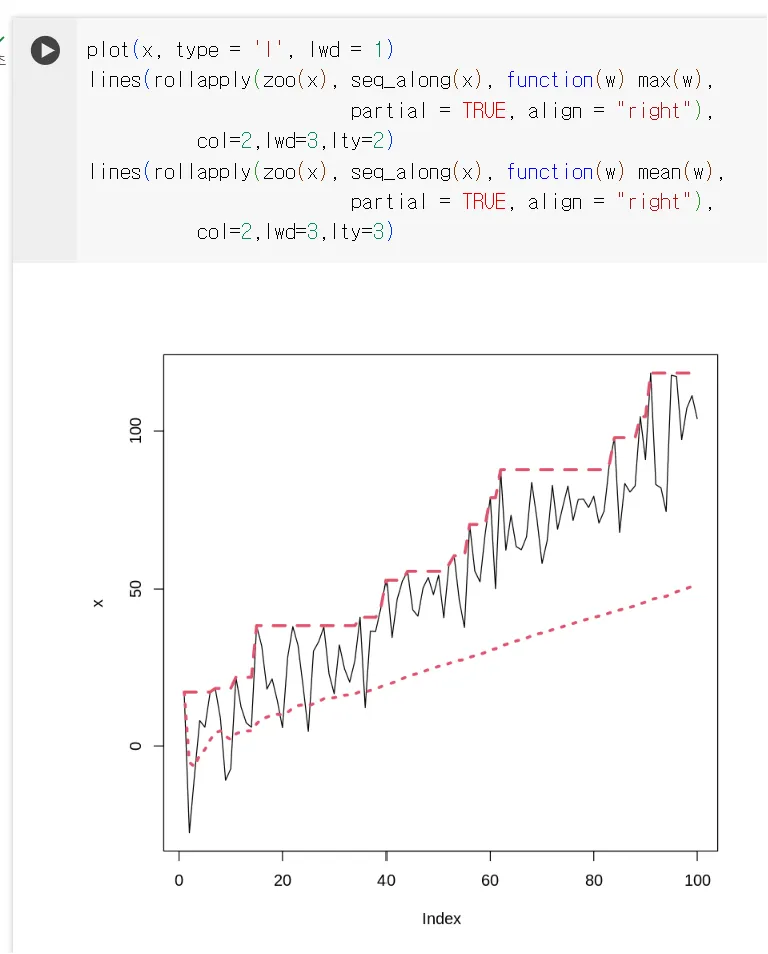
# 확장 윈도우
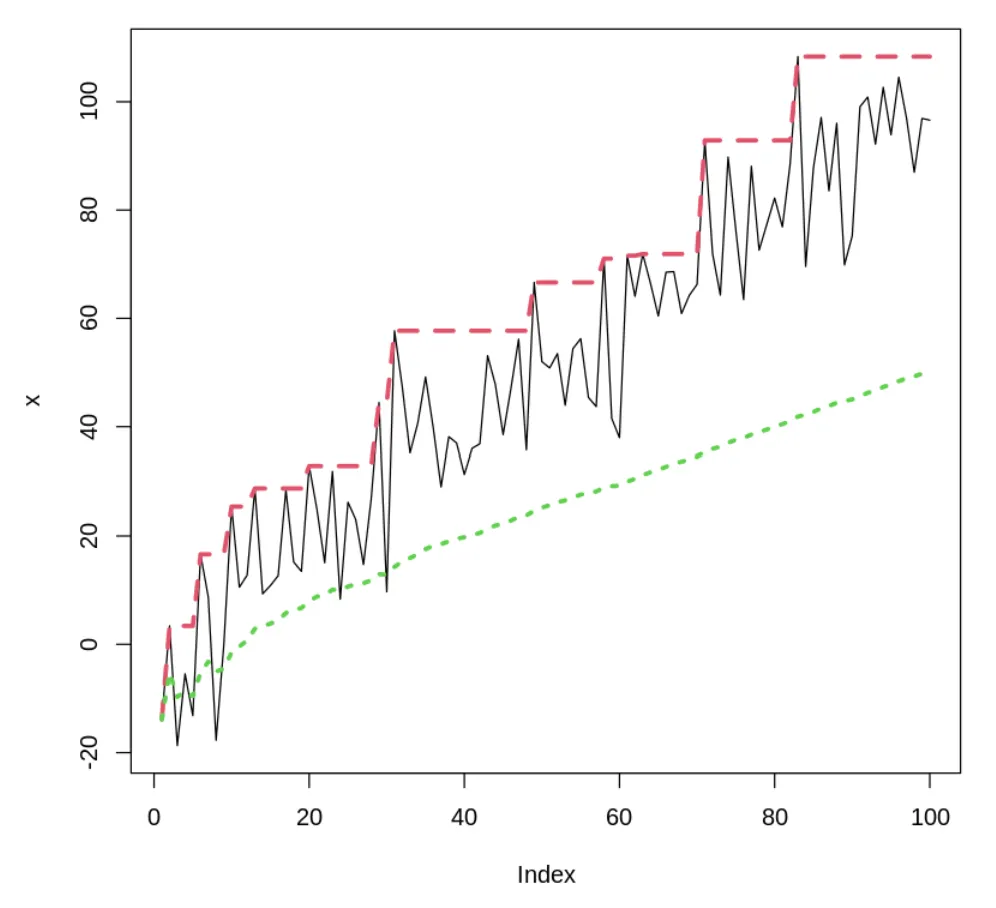
plot(x, type = 'l', lwd = 1)
lines(cummax(x), col = 2, lwd = 3, lty = 2) # 최대값
lines(cumsum(x)/1:length(x), col = 3, lwd = 3, lty = 3) # 평균
R
복사
•
빨강색 선: 최대값, 연두색점선: 평균
•
데이터의 특정 패턴을 나타내는데 사용
•
확장 윈도를 사용하여 계산한 최대값은 시계열 데이터의 전체적인 추세를 고려하여 증가하므로 확장윈도를 단조함수로 볼 수 있음
•
단조함수: 함수값이 증가하거나 감소하는 특성을 가지는 함수
•
확장 윈도의 장기적인 기억 때문에 근본적인 추세가 덜 두드러지고, 보다 부드러운 패턴을 나타냄, 롤링 평균보다 더 낮음
◦
cummax()와 cummin() 함수는 각각 누적 최대값과 누적 최소값을 계산하는 함수
◦
cumsum() 함수를 활용하여 누적 합계를 구할 수도 있음
•
시계열 데이터 x를 선 그래프로 그린후 cummax()함수 사용해 x의 누적 최대값 계산(시계열 데이터에서 각 지점까지의 최대값을 누적하여 계산한 것)
•
cumsum() 함수를 사용해 x의 누적 합계를 계산하고 이를 각 데이터 포인트까지의 평균으로 나누어 평균을 구함
•
첫번째 인수 x는 롤링 통계량을 계산할 데이터 자체
•
두번째 인수seq_along(x)는 데이터 x의 길이에 따라 순차적인 정수를 생성,
해당 데이터의 길이에 따라 윈도의 크기를 동적으로 조정하는 인자로 사용
◦
function(w) max(w)는 각 이동 창에 대해 최대값을 계산하는 함수를 정의
◦
function(w) mean(w)는 각 이동 창에 대해 평균을 계산하는 함수를 정의
사용자 정의 롤링 함수
•
적용 가능한 상황에서만 고려해야 함
•
특정 도메인 지식이 유용한 상황에서 특히 유용하게 사용될 수 있음
•
도메인 지식 활용
◦
주식 시장 데이터에서는 이동 평균 이상의 지표를 사용하여 특정 패턴을 탐지
•
노이즈 제거
◦
데이터에서 출렁이는 장치의 노이즈와 같은 추세가 없는 패턴을 제거하기 위해
◦
시계열 데이터의 신호와 노이즈를 분리하고 깨끗한 신호를 추출
•
패턴 탐지
◦
혈당 증가와 같은 단조로운 패턴을 탐지하여 건강 상태를 모니터링하는 데 사용
3.2.3 자체상관의 파악과 이해
•
‘자체상관’: 특정 시점의 값이 다른 시점의 값과 상관관계가 있다
ex) case1: 5월15일의 온도가 높아질때 8월15일의 온도도 같이 높아지는 상관관계(상관관계 有)
case2: 5월15일의 온도 정보만으로는 8월15일의 온도 범위의 어떤 정보도 알 수 없음(상관관계 無)
•
‘자기상관’: 특정 시점에 고정되지 않으며 자체상관을 일반화한 것, 특정 시점에 고정거리를 갖는 두 시점에 상관관계가 존재하는지와 같은 좀 더 일반적인 질문을 던져 볼 수 있음
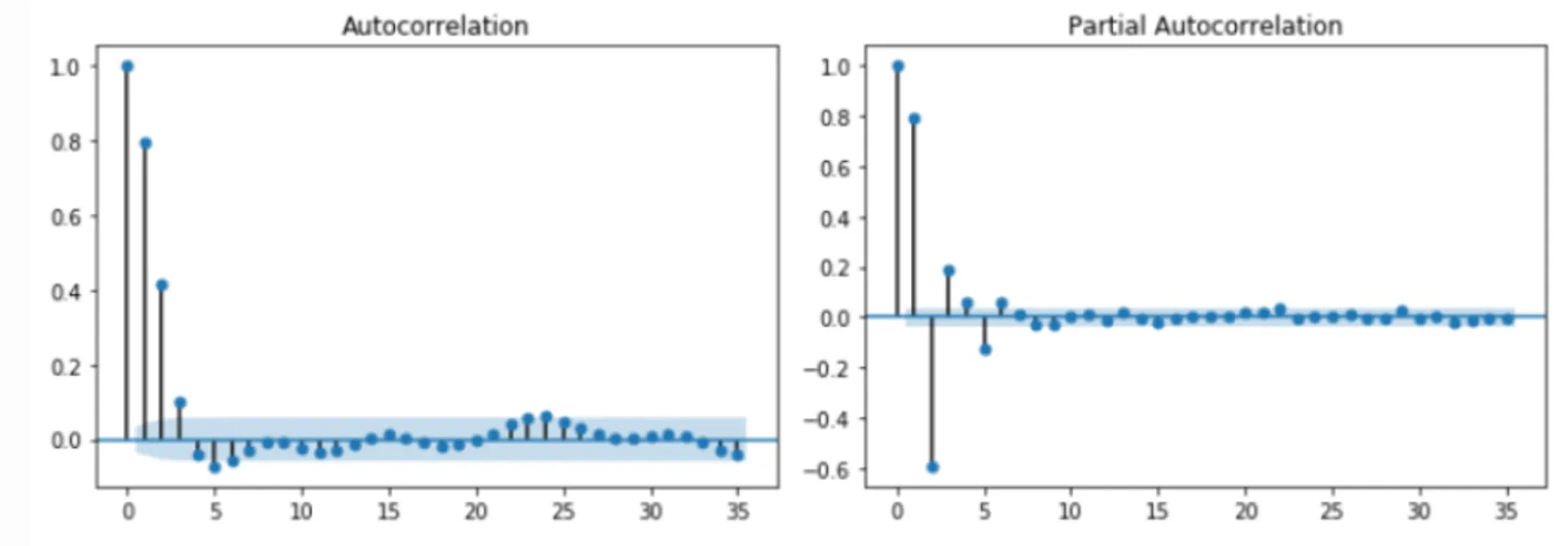
시계열 데이터의 성질을 분석하는데 있어서 중요하게 활용되고 있는 것이 상관도표(Correlogram) 상관도표는 Auto Correlation Function(ACF)과 Partial Auto Correlation Function(PACF) 중 하나를 그래프로 표현한 것.
상관도표를 활용하여 현 시점의 자료와 시점의 차이(lag)를 가지는 자료를 비교하여 어떤 관계를 가지고 있는지를 분석할 수 있음.
즉, 상관도표를 활용하여 시점의 차이의 영향력을 알아볼 수 있음.
자기상관(Auto Correlation) 기능
•
‘계열 상관’이라고도 알려져 있음
어떤 신호와 자신을 지연함수로 시간상 지연 이동한 신호 간의 상관관계
•
상관값이 두 변수 사이의 선형 관계의 크기를 측정하는 것처럼 자기상관은 시계열의 시차 값(Lagged Values) 사이의 관계를 측정
•
시간의 흐름에 따라 독립적이지 않고 과거의 데이터의 영향을 받는 상관관계
ex) 오늘 주식의 가격이 어제 가격에 영향을 받고 내일의 가격에 영향을 줌 → 이러한 경우 시계열 자료는 자기상관관계를 갖는다
시간에 따른 상관 정도를 나타내기 위해 사용하는 통계량 → 자기 상관 함수
자기 상관 함수(Auto Correlation Func, ACF) 특징
시간에 따른 상관 정도를 나타내기 위해 사용하는 함수
•
ACF의 주기성 = 원래 과정 주기성
•
주기 함수들의 합의 자기 상관 = 각 개별 함수에 대한 자기 상관의 합
•
시차 = 0 인경우, 모든 시계열의 자기 상관 계수 = 1
•
ACF는 양과 음의 시차에 관해서 대칭
•
0이 아닌 유효한 ACF 추정을 결정하는 통계적 규칙은 +/-1.96 x sqrt(n)의 임계영역 사용하는 것
편자기 상관 함수(Partial Auto Correlation Func, PACF) = 부분 자기 상관 함수
•
어떤 것들에 대한 상관관계를 보려고 할 때, 그에 영향을 주는 요소들을 제외하고 상관관계를 볼 때 PACF 를 이용
•
자신에 대한 그 시차의 편상관
•
두 시점 사이에 존재하는 모든 정보 고려
편자기 상관 함수(PACF) 특징
시간에 따른 시차의 편상관정도를 나타내기 위해 사용하는 함수
•
어떤 데이터가 유용한 정보를 가지고, 어떤 데이터가 단기간의 고조파인지 보여줄 수 있음
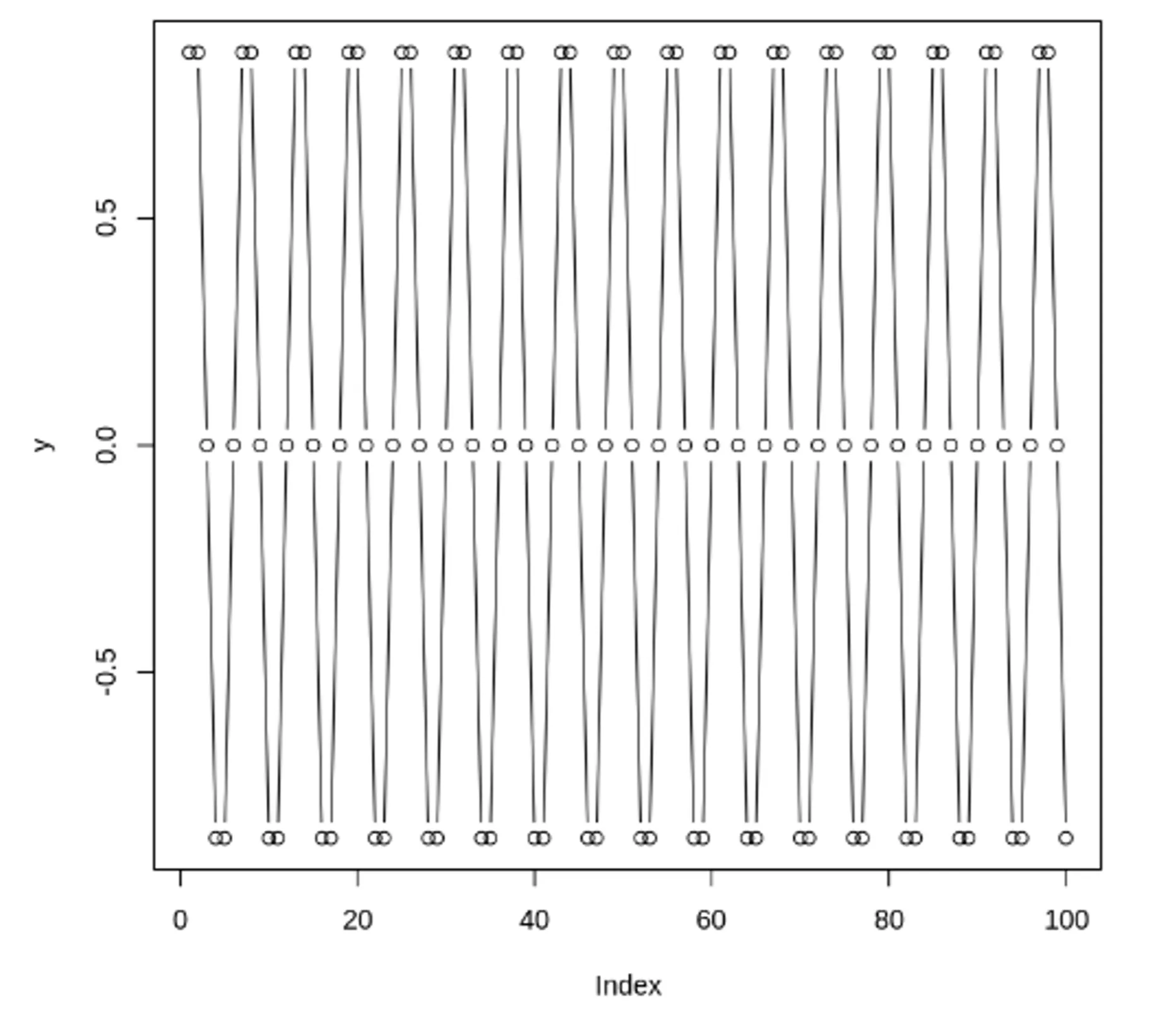
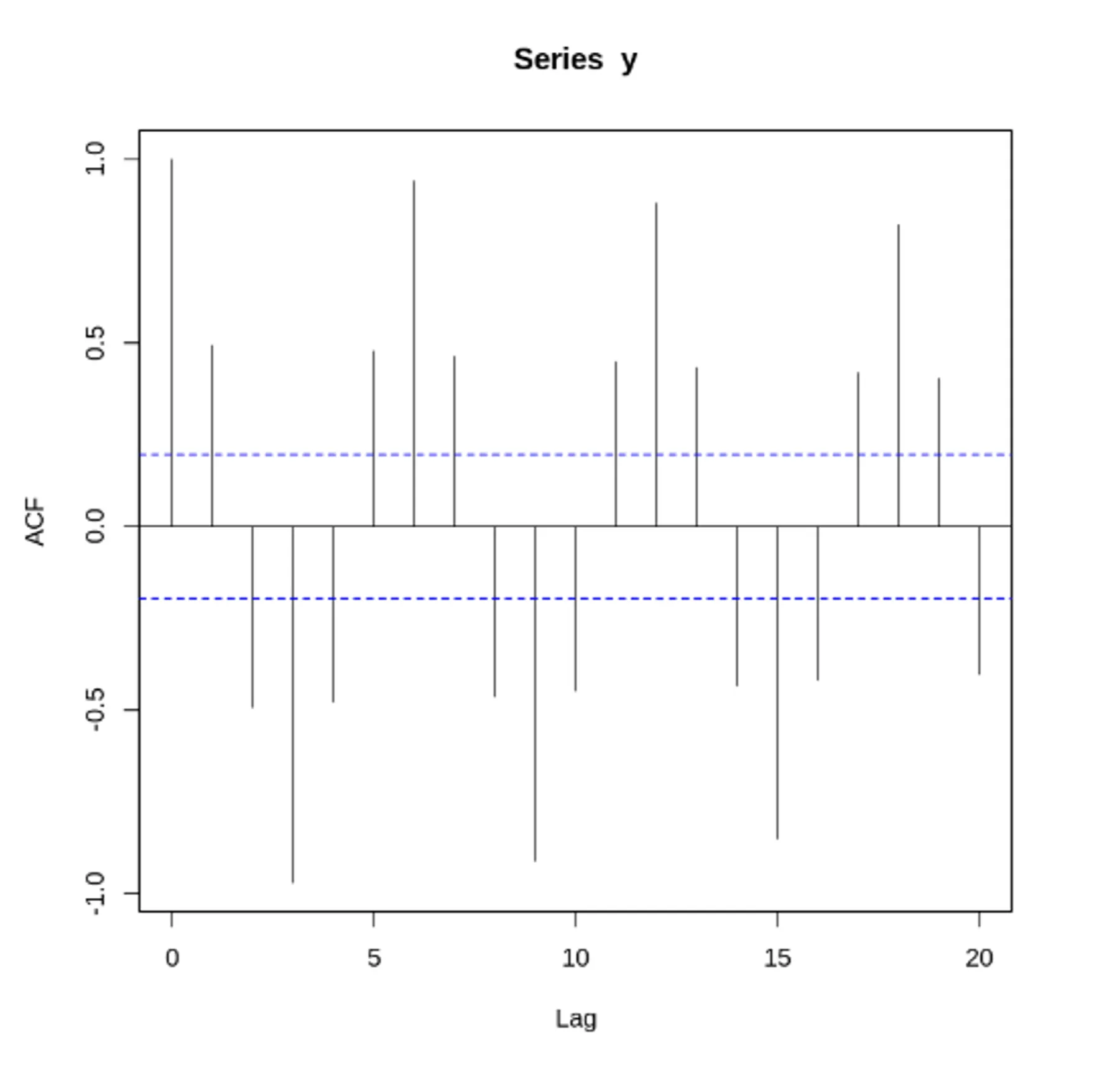
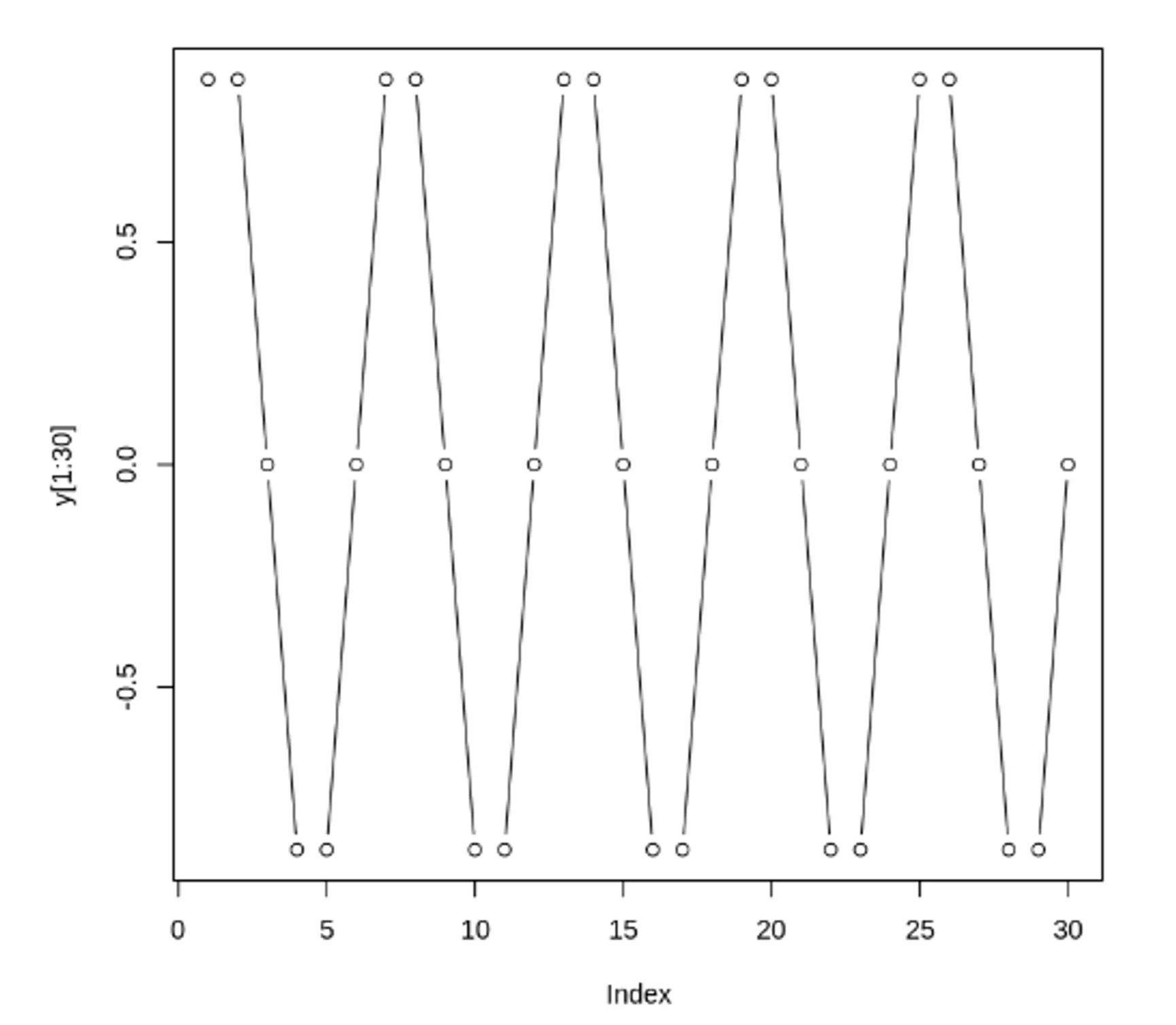
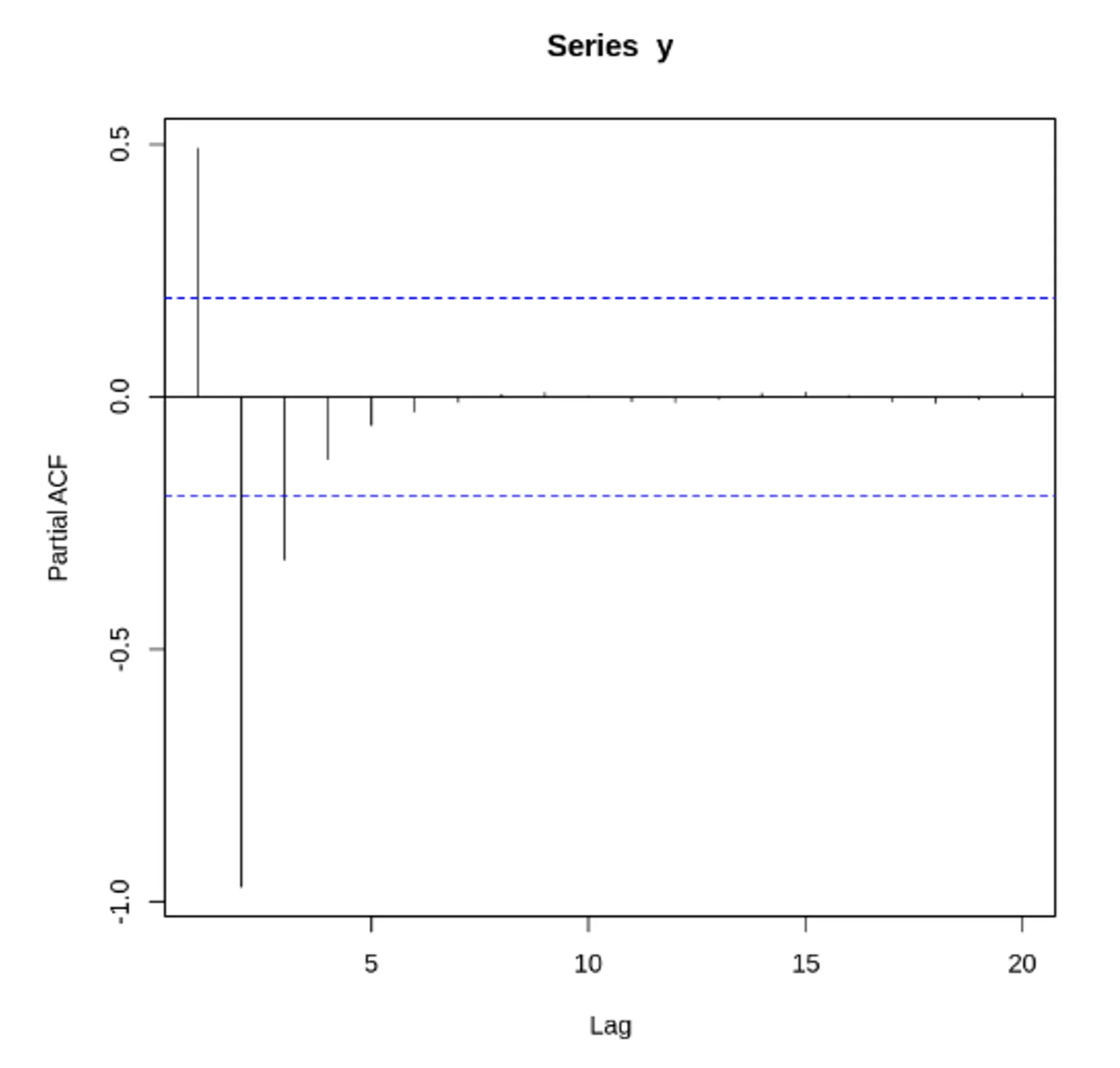
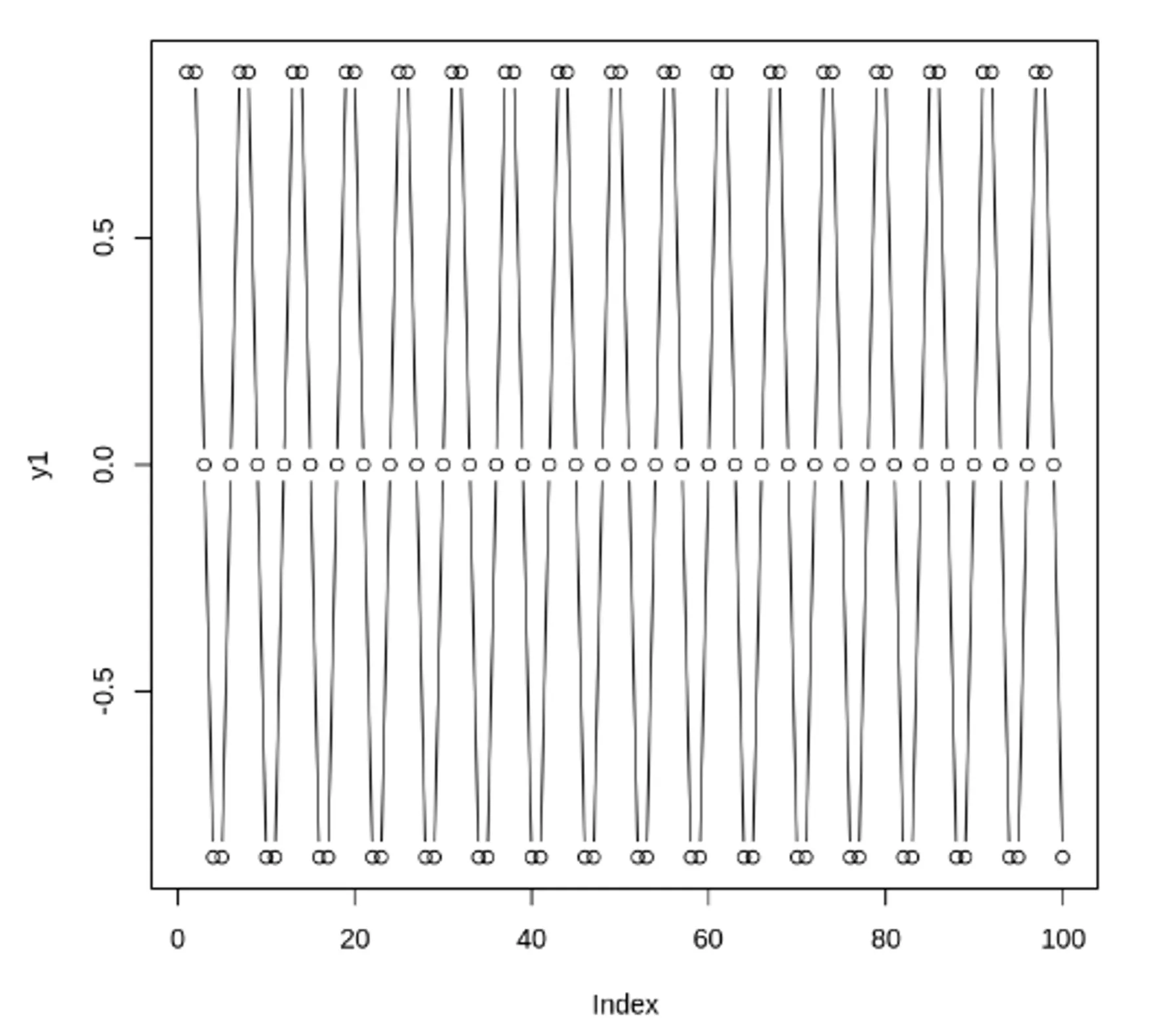
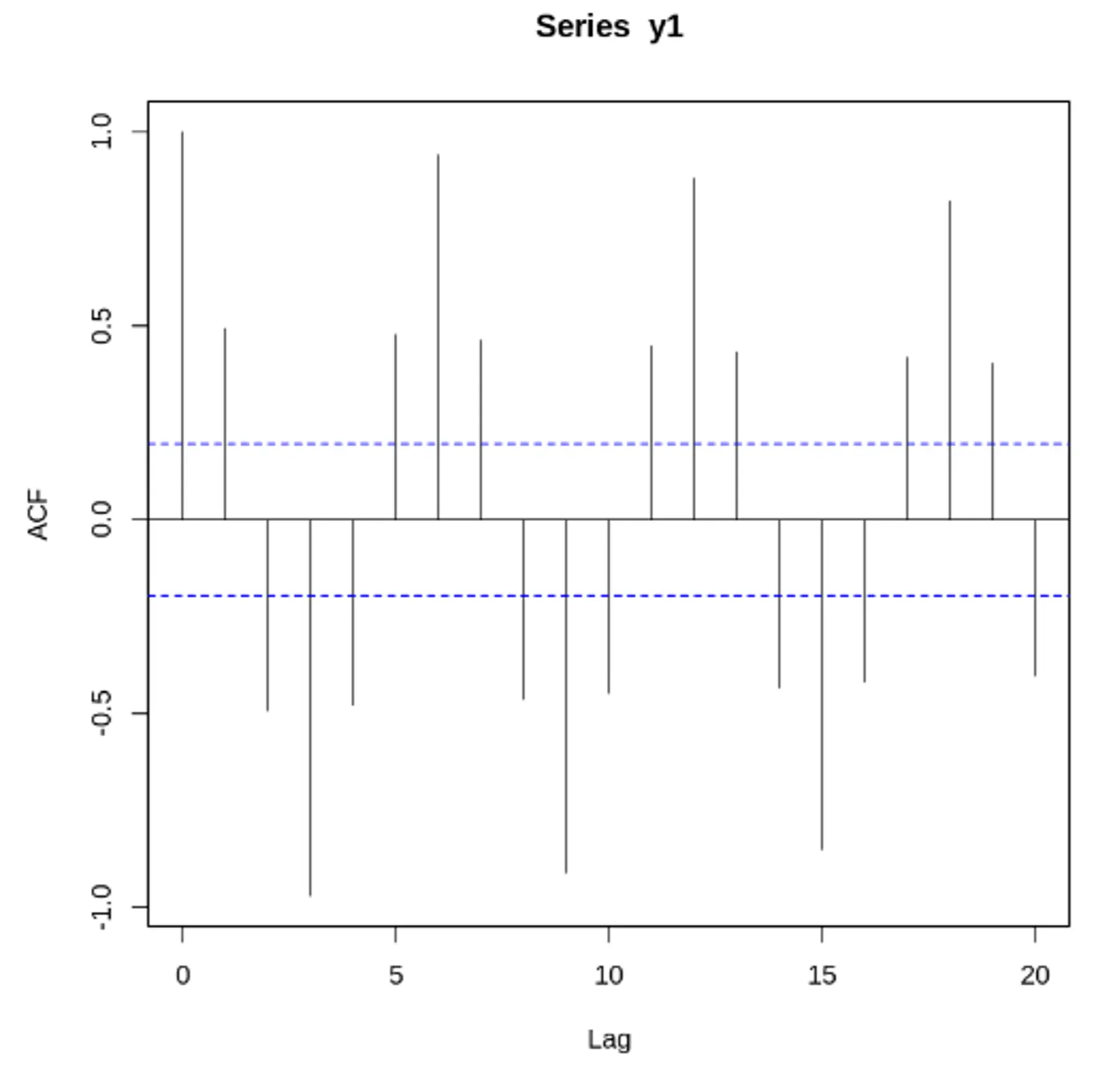
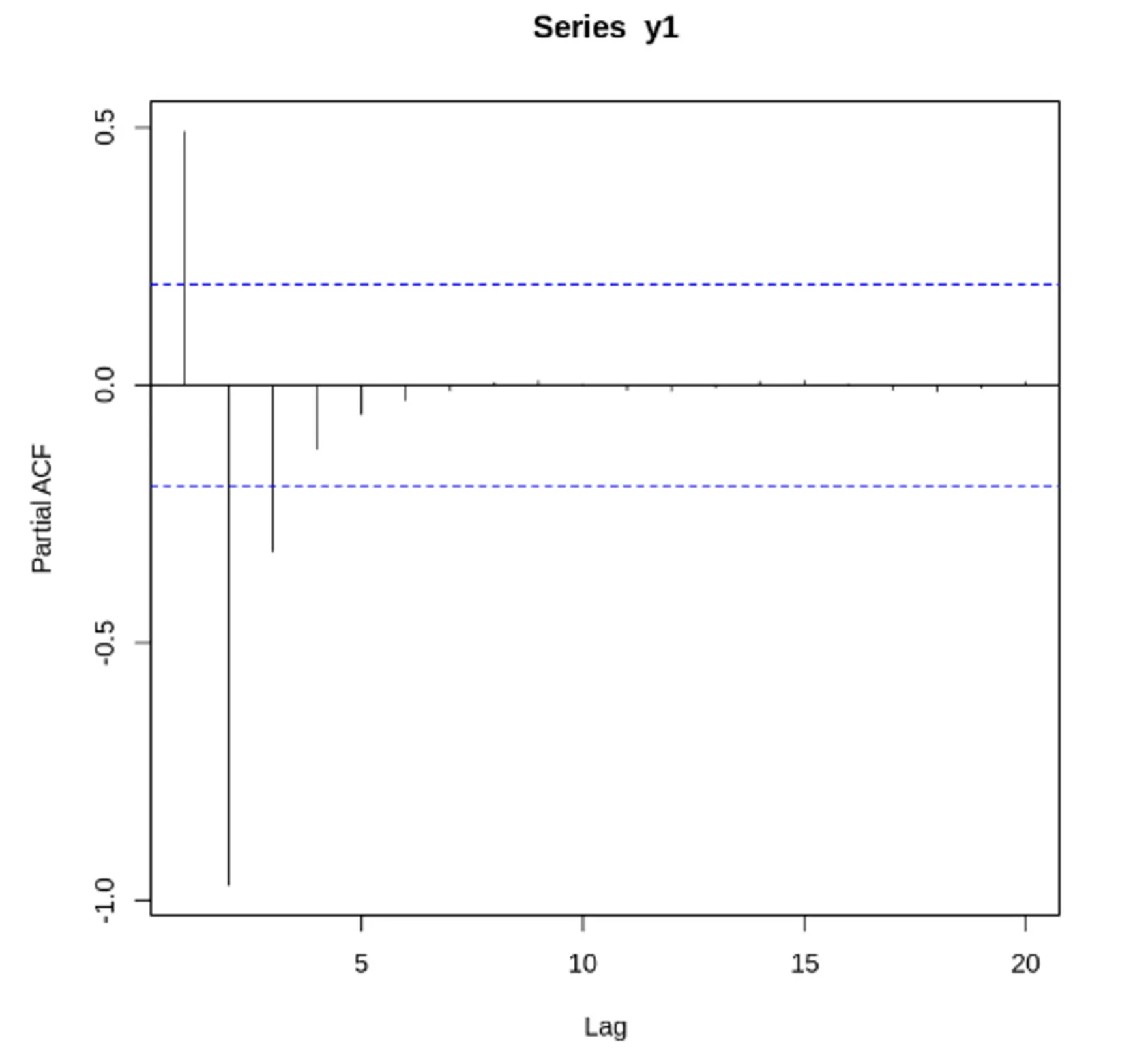
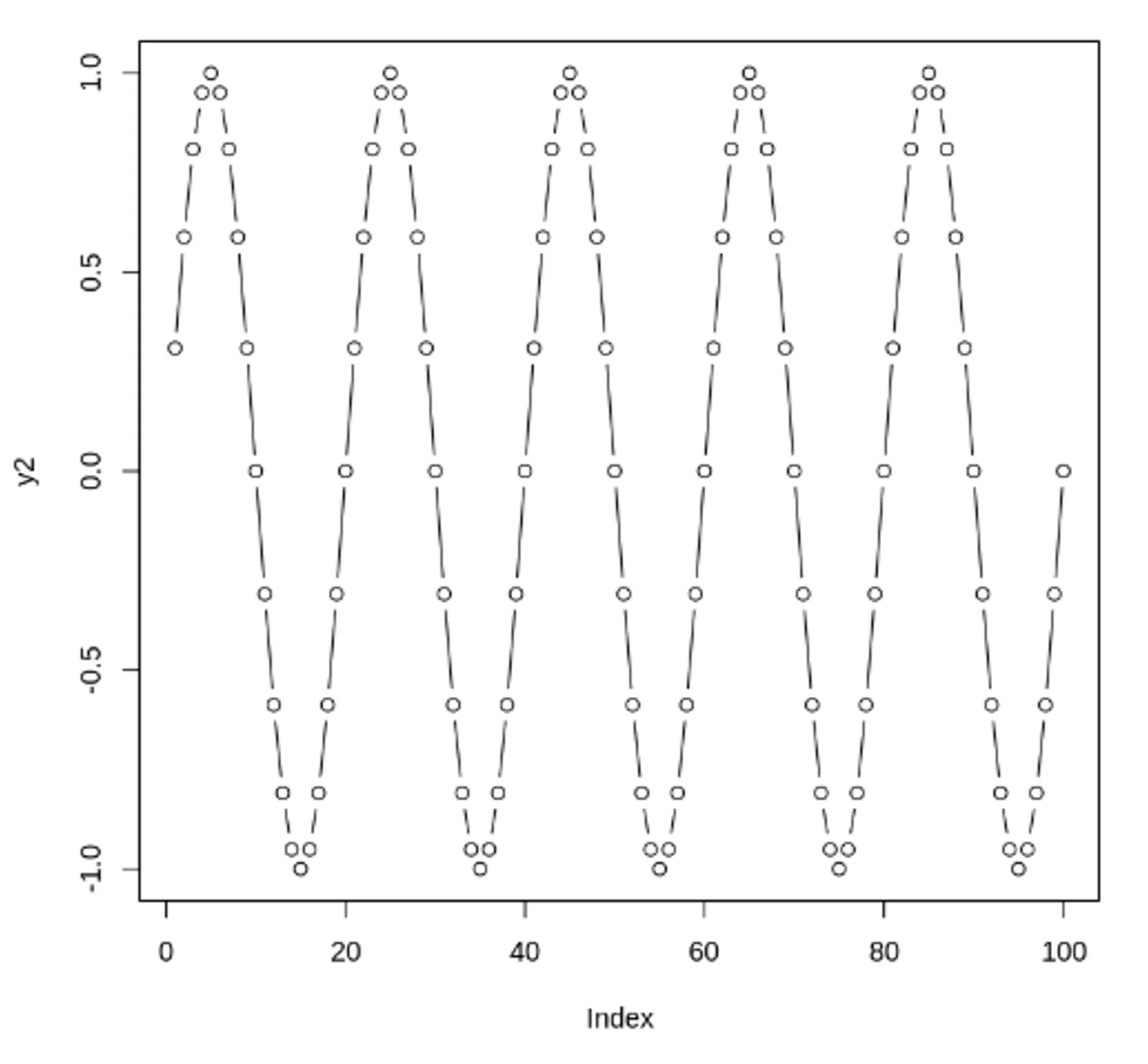
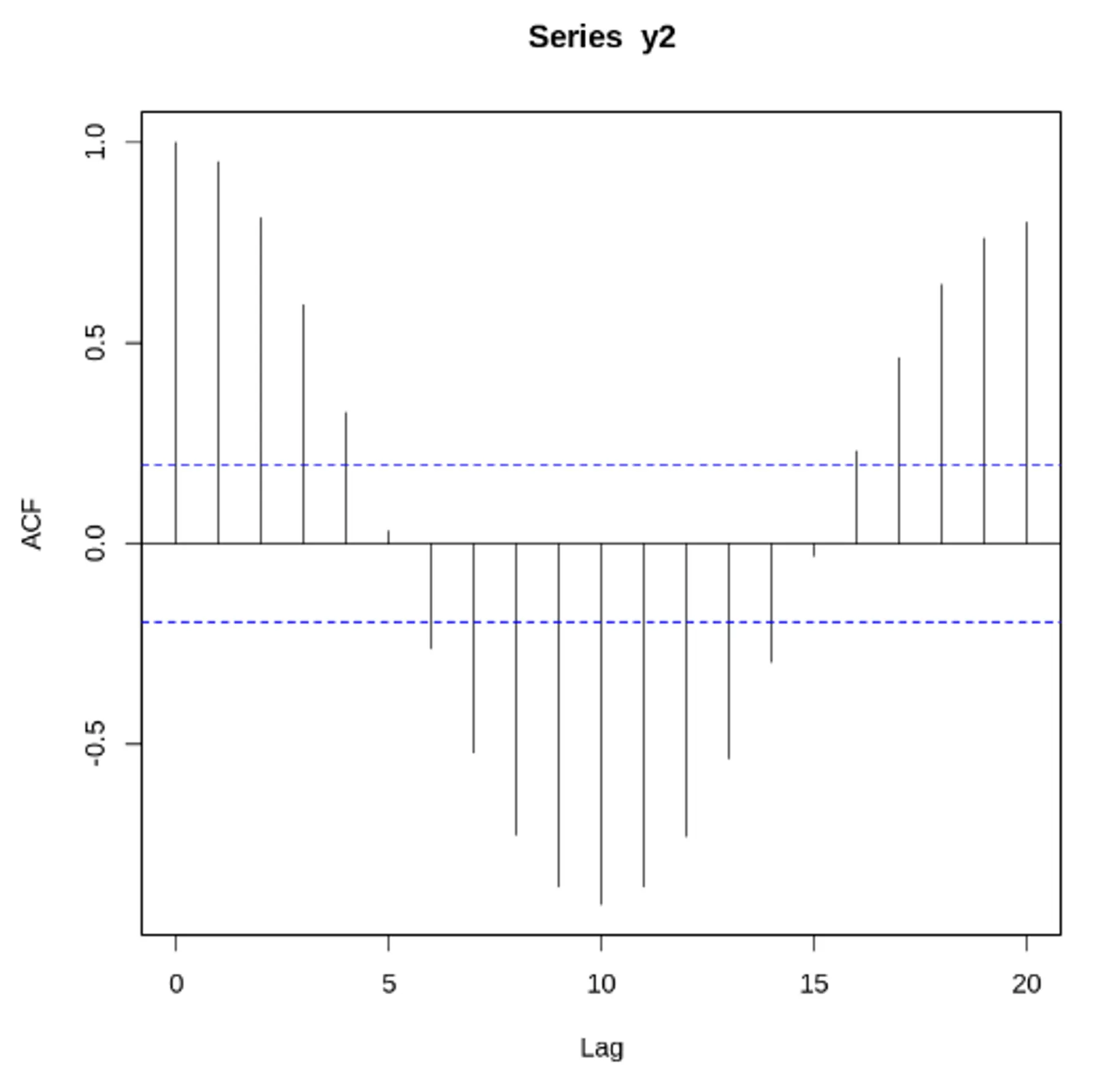
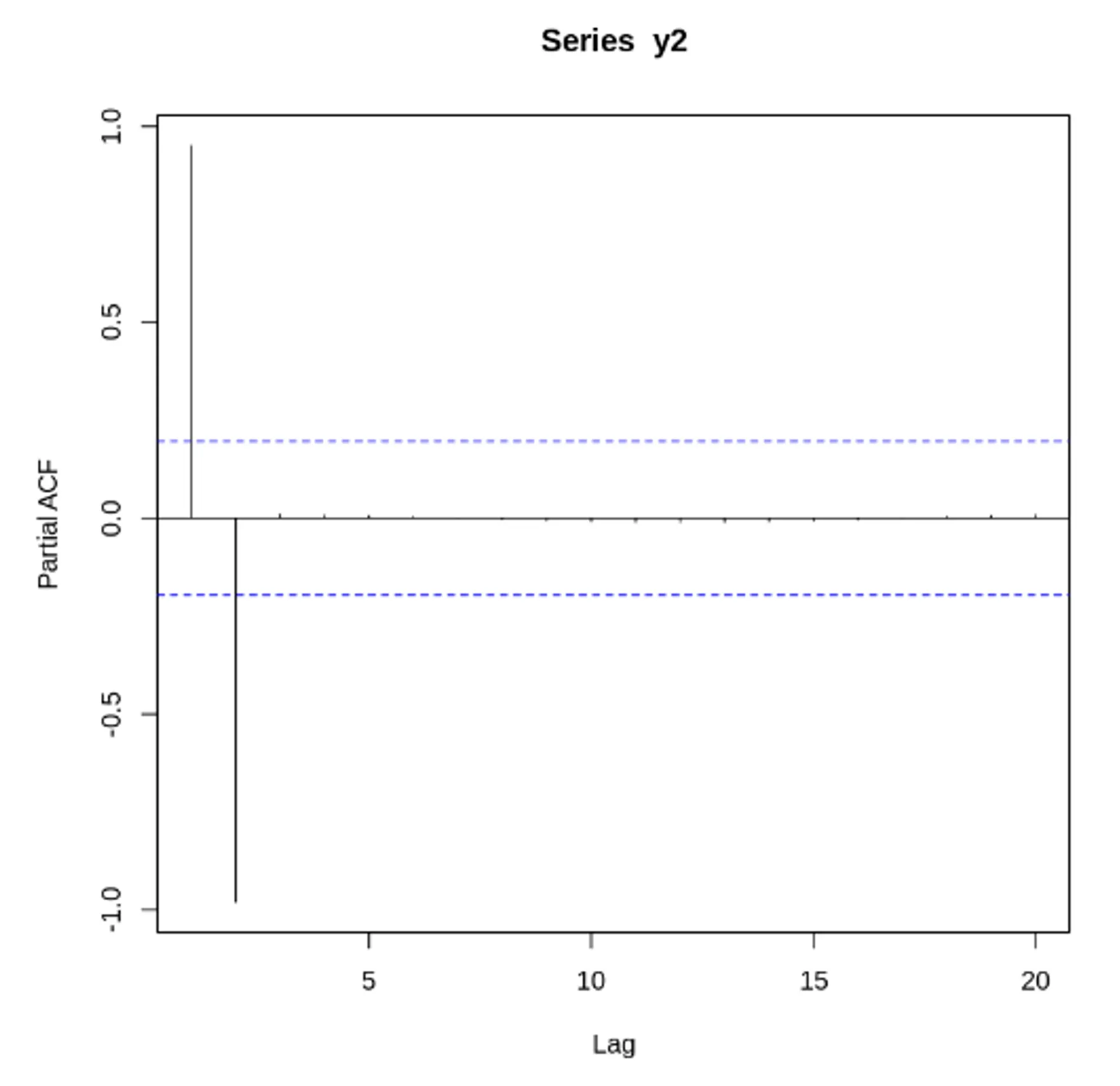
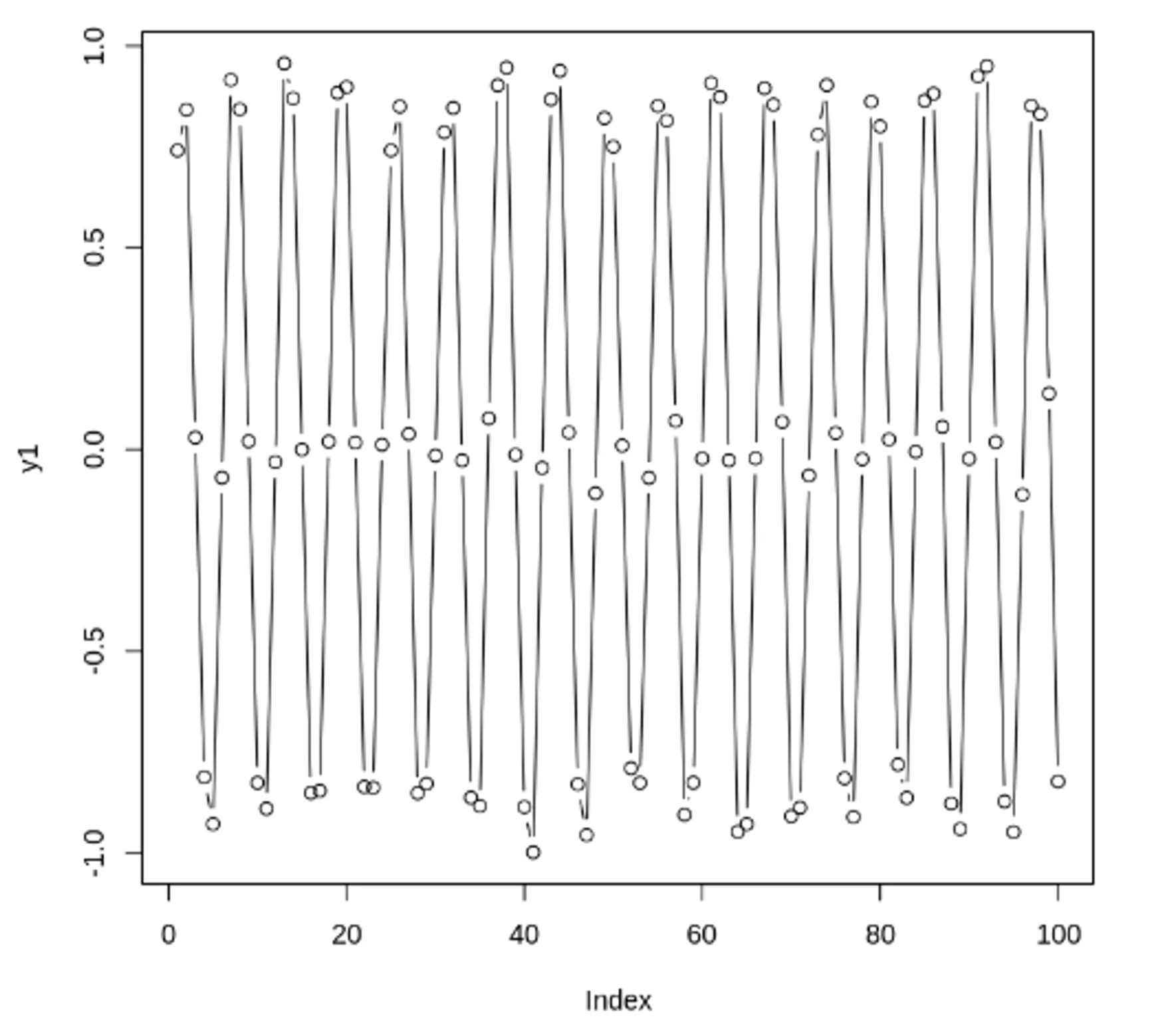
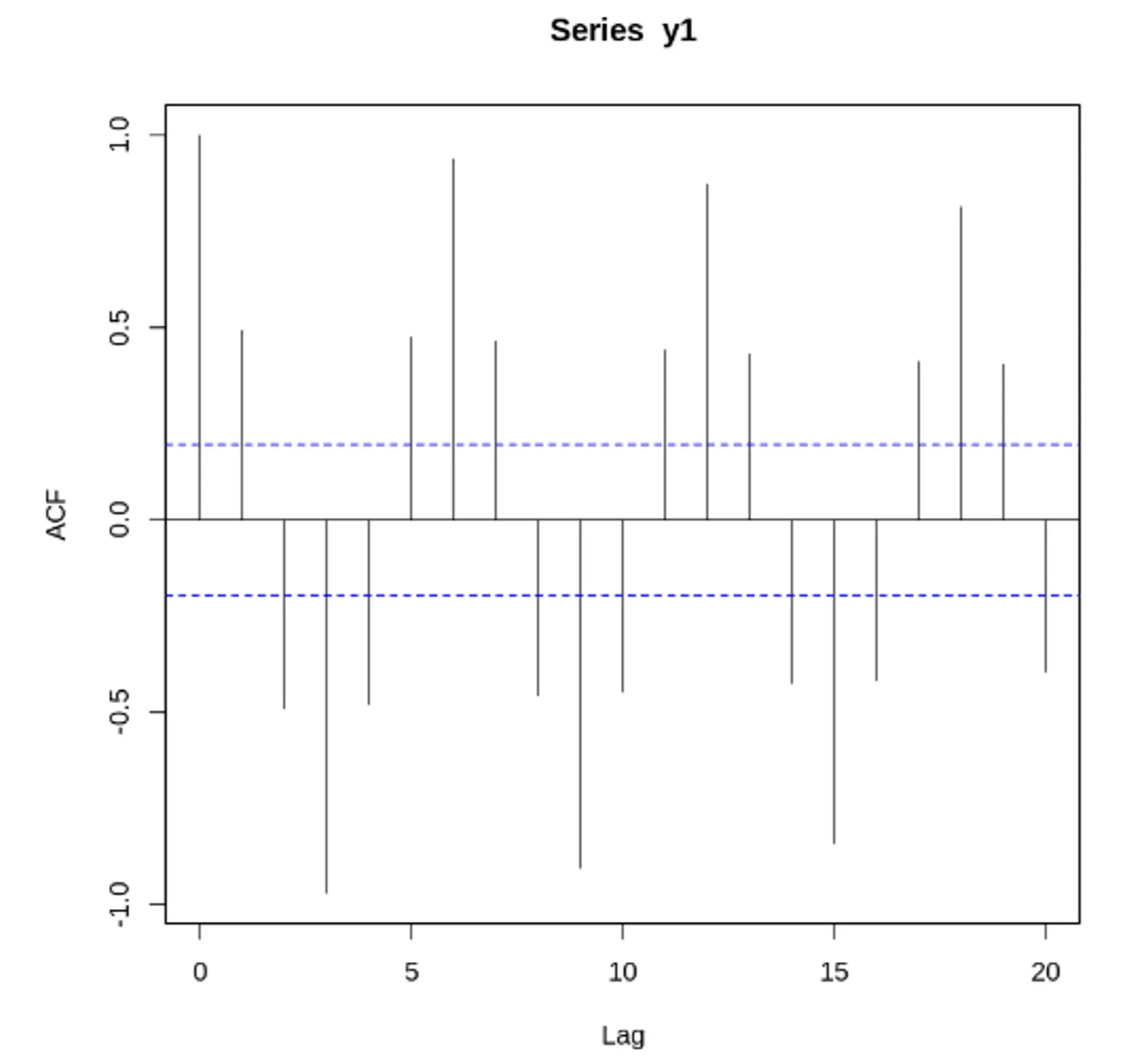
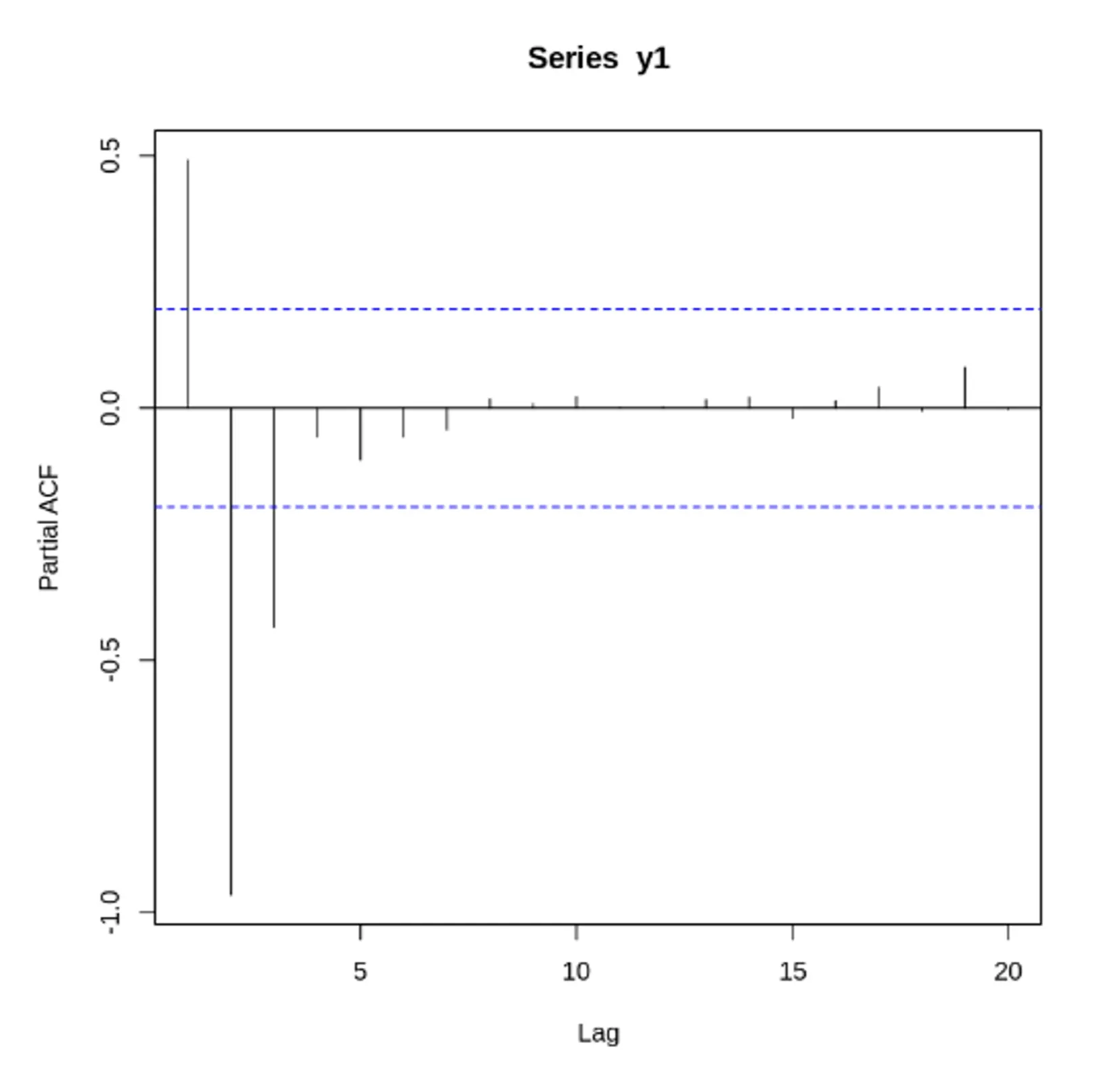
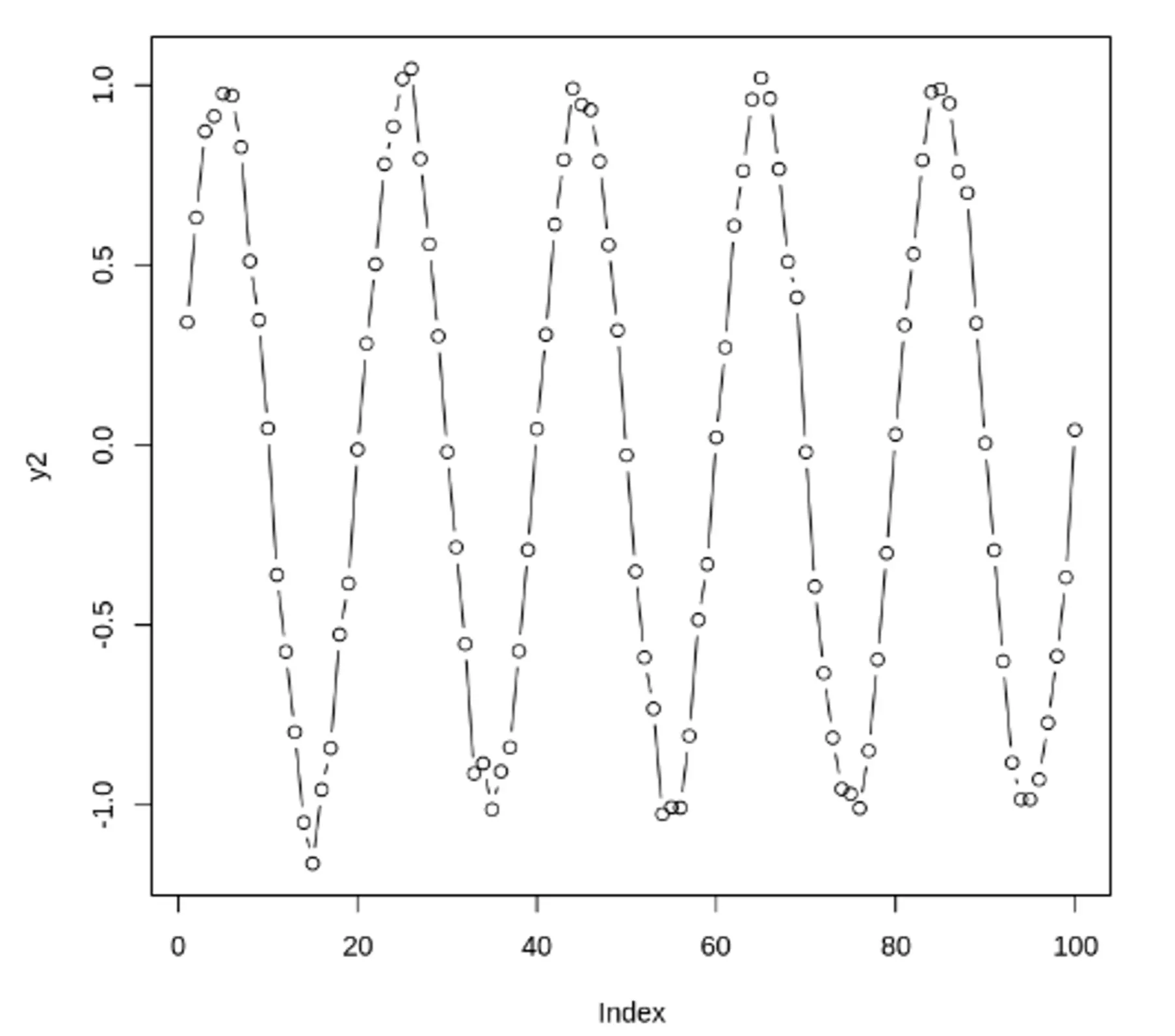
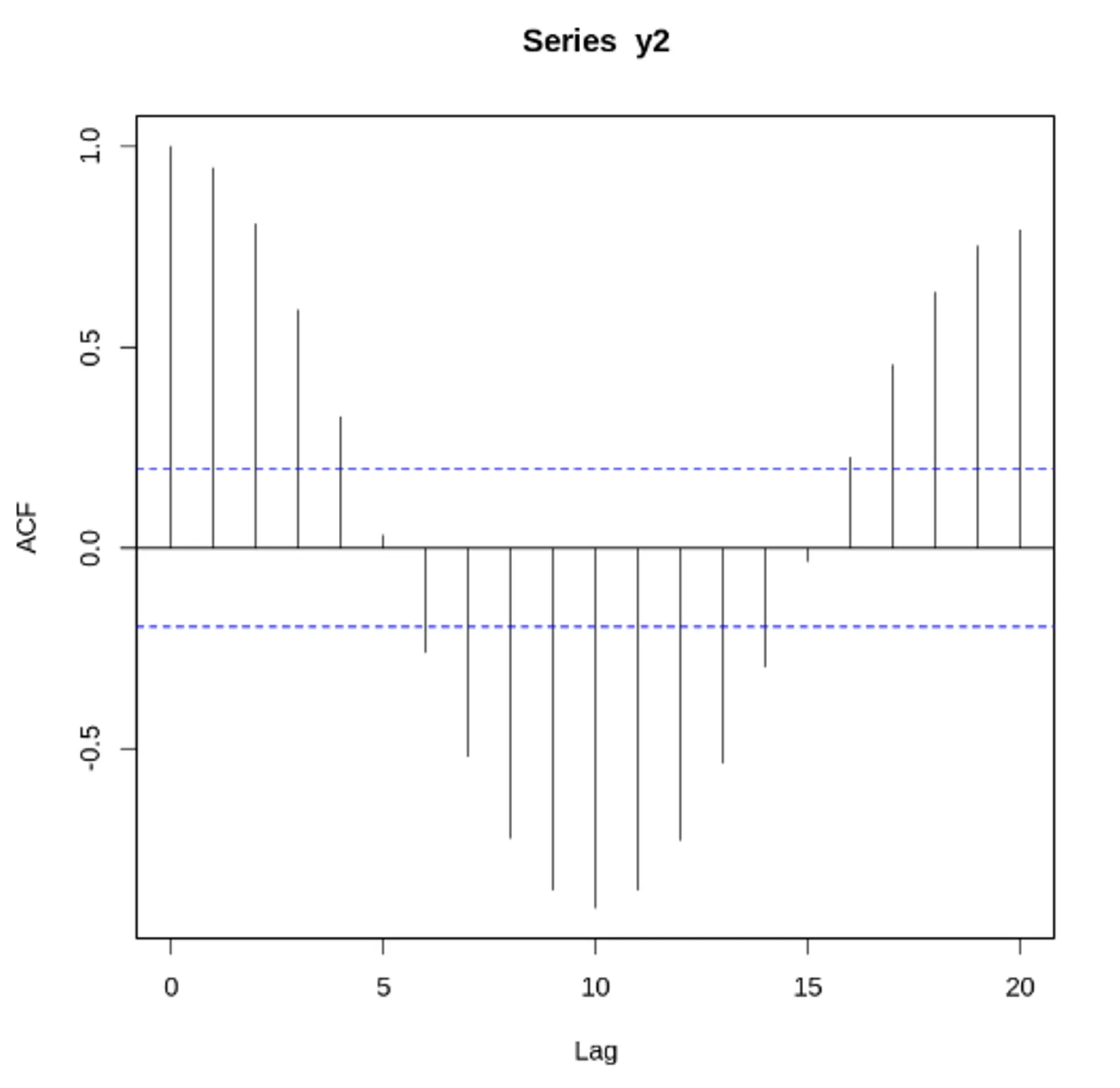
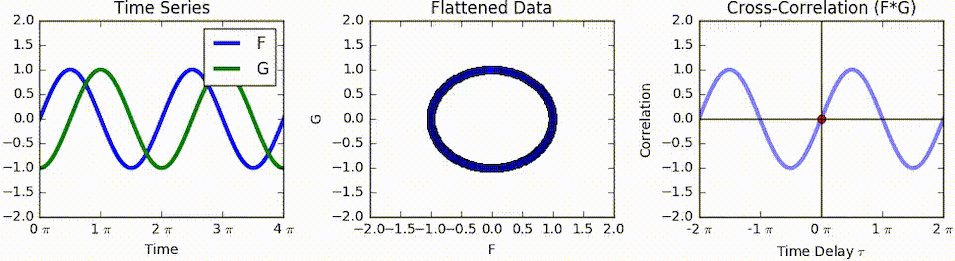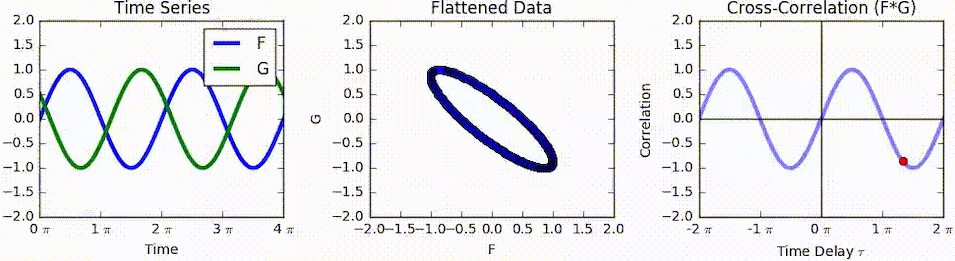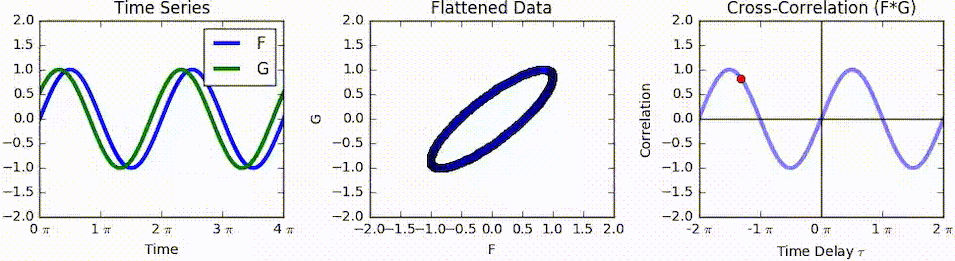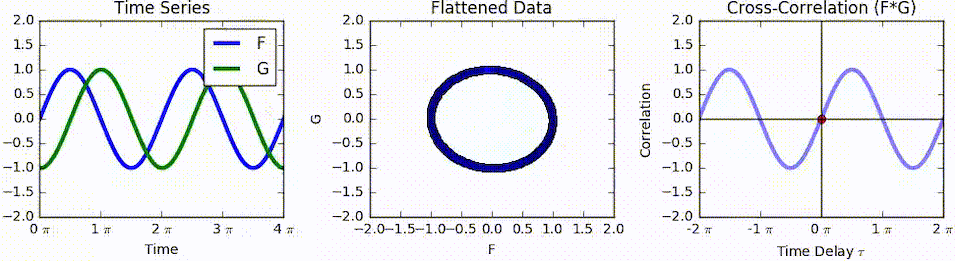
자기 상관 함수(ACF) VS 편자기 상관 함수(PACF) - 노이즈가 없는 경우
두 사인 함수와 각 함수에 대한 ACF, PACF 도표
정상 데이터의 ACF는 0으로 빠르게 떨어져야함. 비정상 데이터의 경우, 시차가 1일 때의 값은 큰 양수
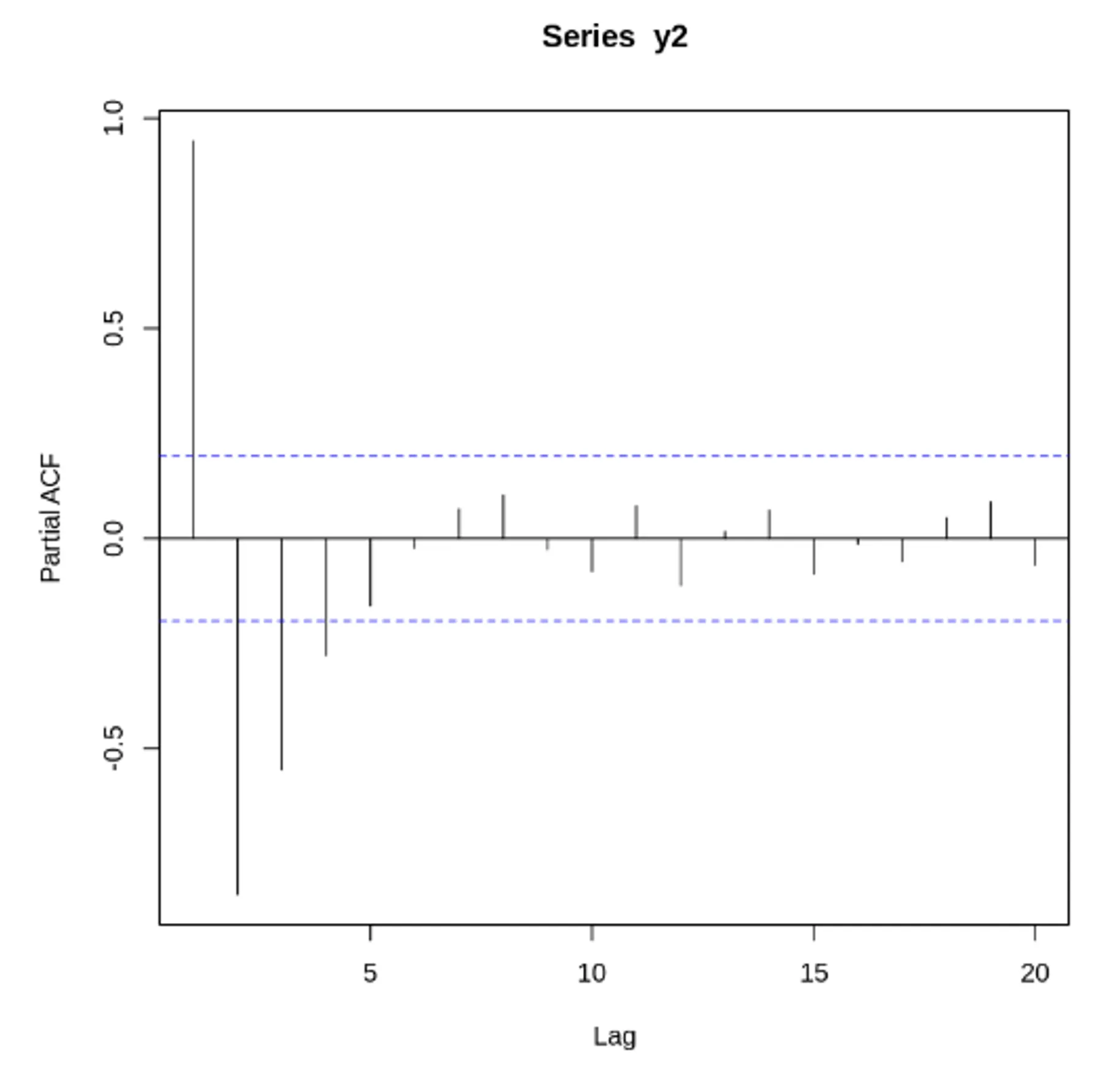
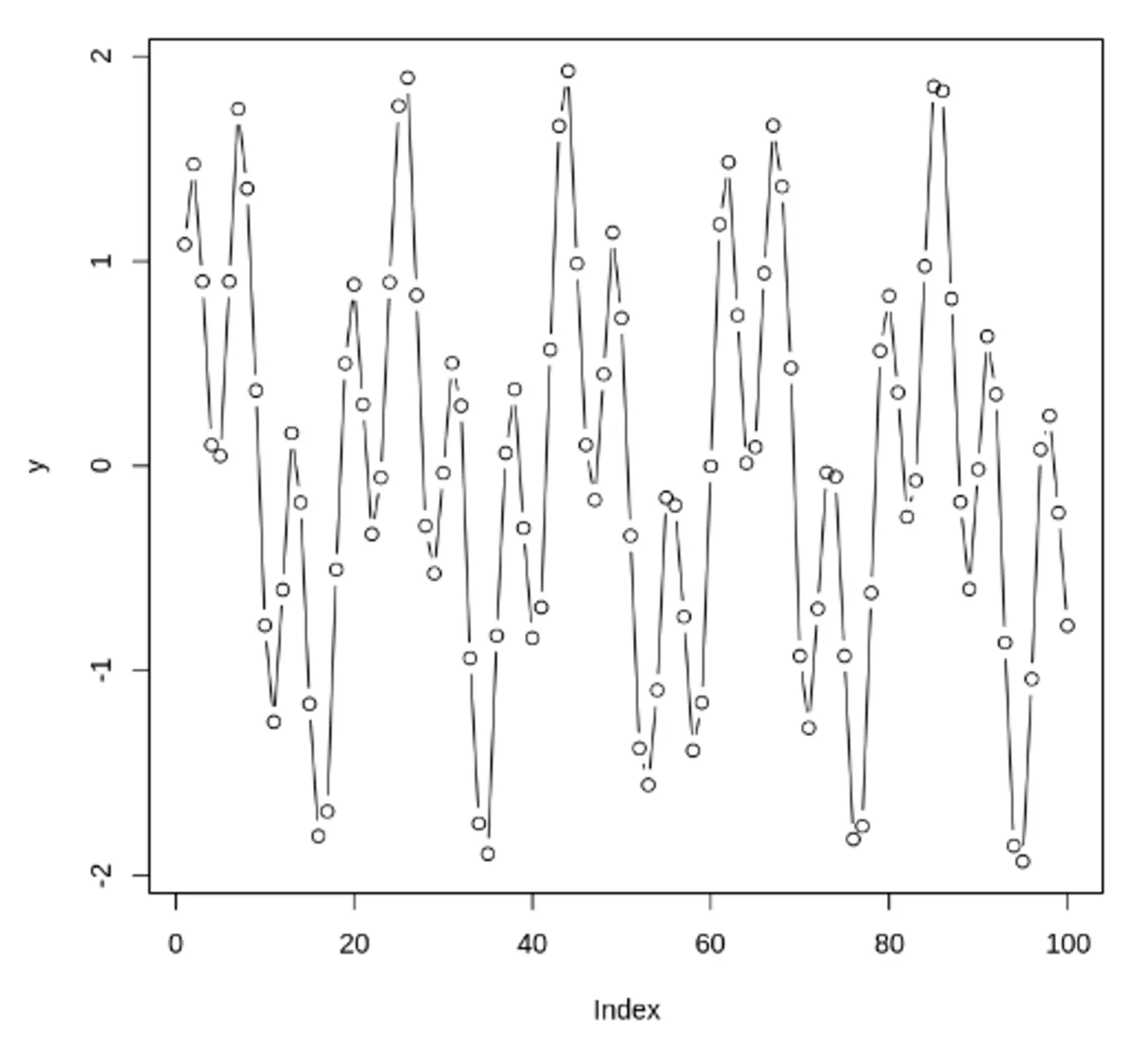
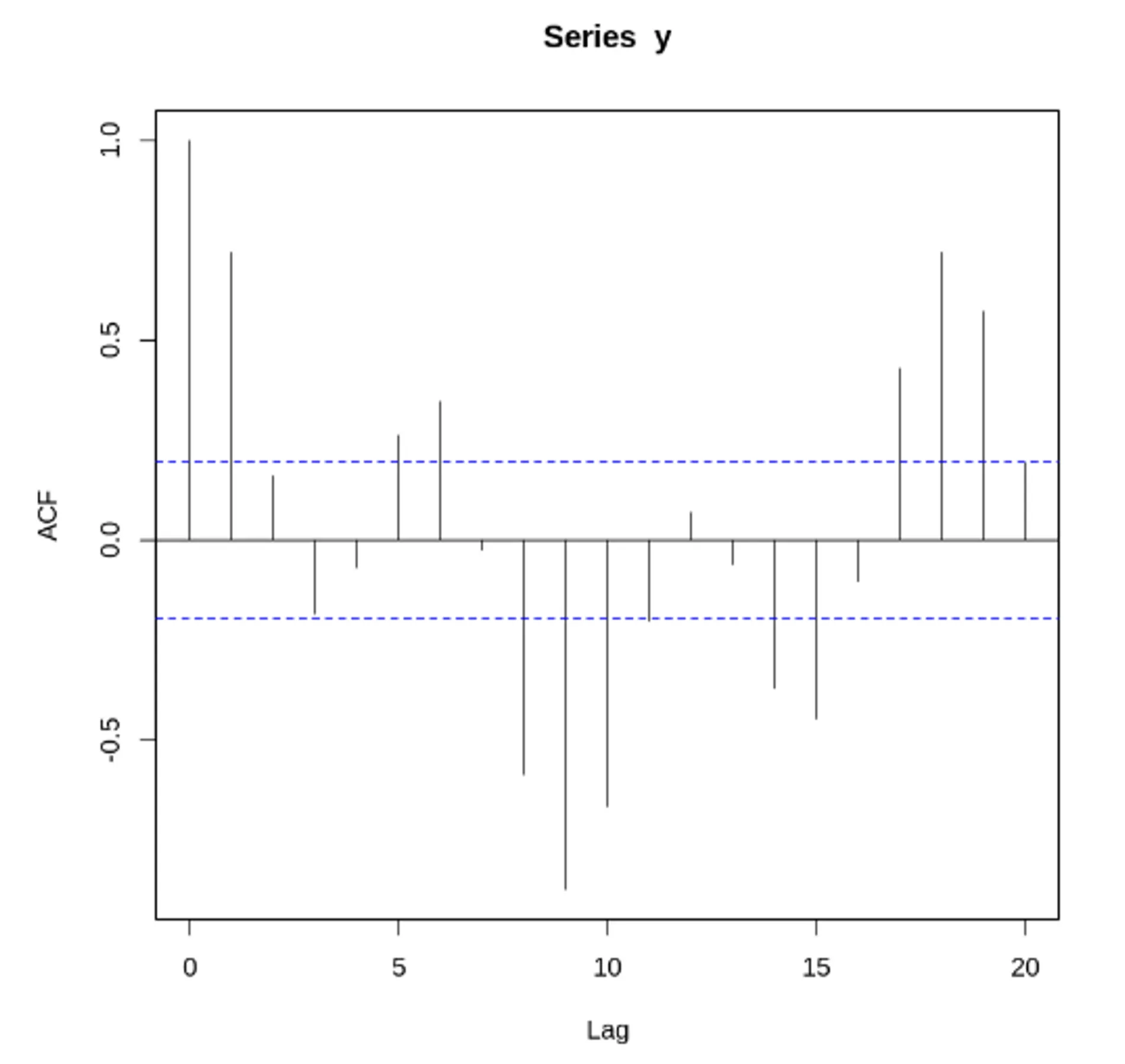
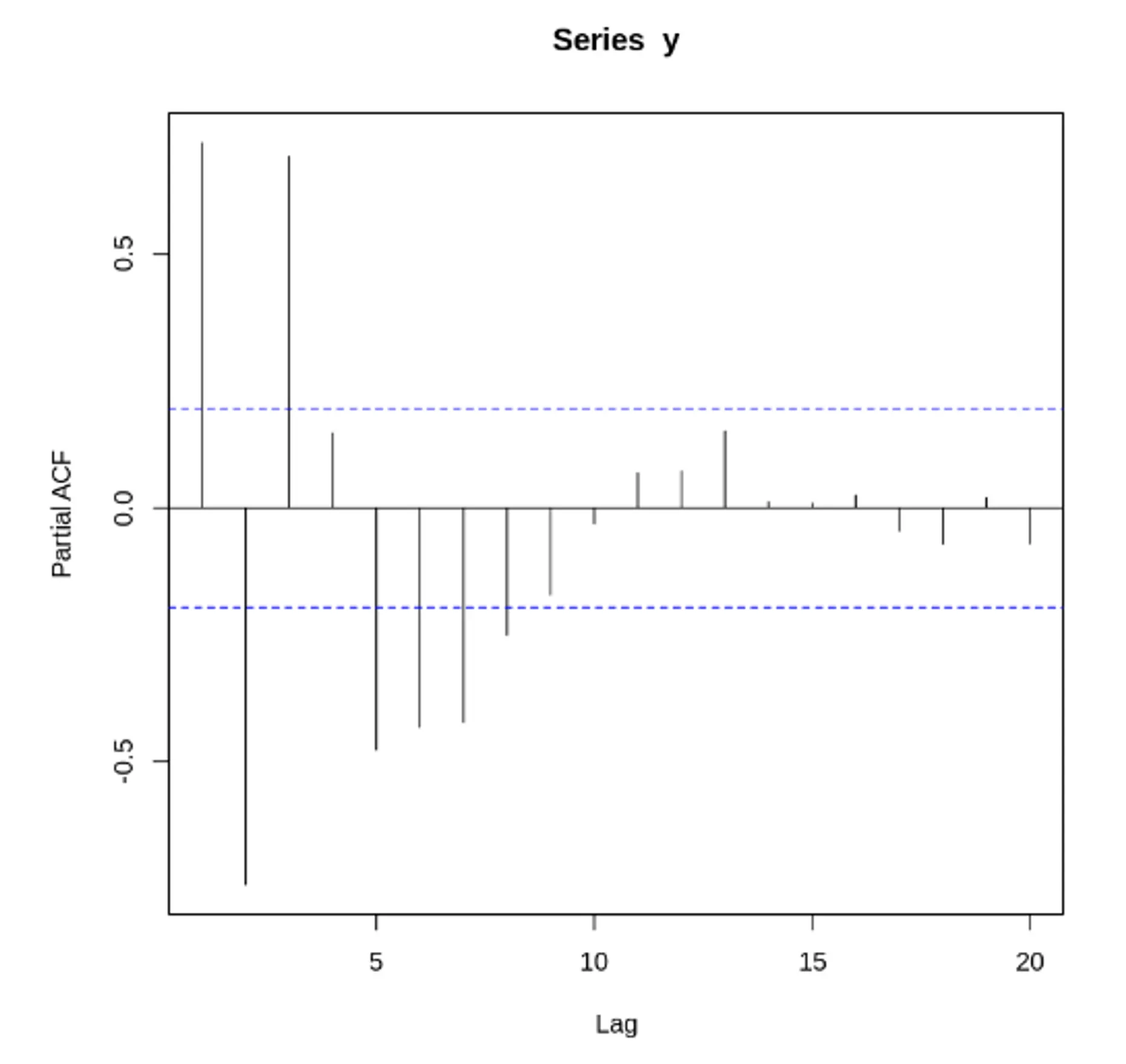
자기 상관 함수(ACF) VS 편자기 상관 함수(PACF) - 노이즈가 있는 경우
노이즈가 많은 두 사인 곡선과 이 둘의 합. ACF, PACF 도표
결론
•
어느 시점까지의 데이터가 현재 시점에 영향을 주는지 연산하는 함수
•
AR, MR 모델 적합성을 설정할때 필요한 함수(절단값으로 설정됨)
절단값: 아래 그림 중 값이 파란색 부분으로 들어오기 직전의 값
AR/MA 모형과 ACF/PACF 의 관계
AR(p) | MA(q) | |
ACF | 점차적으로 감소 | 시차 q 이후에 0 |
PACF | 시차 p 이후에 0 | 점차적으로 감소 |
참고
AR (Autoregression / 자기회귀)
•
이전 관측값의 오차항이 이후 관측값에 영향을 주는 모형
P 시점 전의 값이 현재 값에 영향을 줌
ex) ar(1)은 1시점 전에 의해 현재시점이 영향을 받는 모형, ar(2)는 2시점 전까지에 의해 현재 시점에 영향을 주는 모형
MA(Moving Average / 이동평균 모형)
•
관측값이 이전의 연속적인 오차항의 영향을 받는다는 모형
데이터의 평균값 자체가 시간에 따라 변화하는 경향을 시계열 모형으로 구성 한 것 ex) ACF는 3시점 이후 절단점을 보이고 PACF가 빠르게 감소하면 MA(2) 모형이라고 볼 수 있음
참고사이트
3.2.4 허위상관
허위 상관(Spurious Correlation)을 나타내는 시계열의 특징
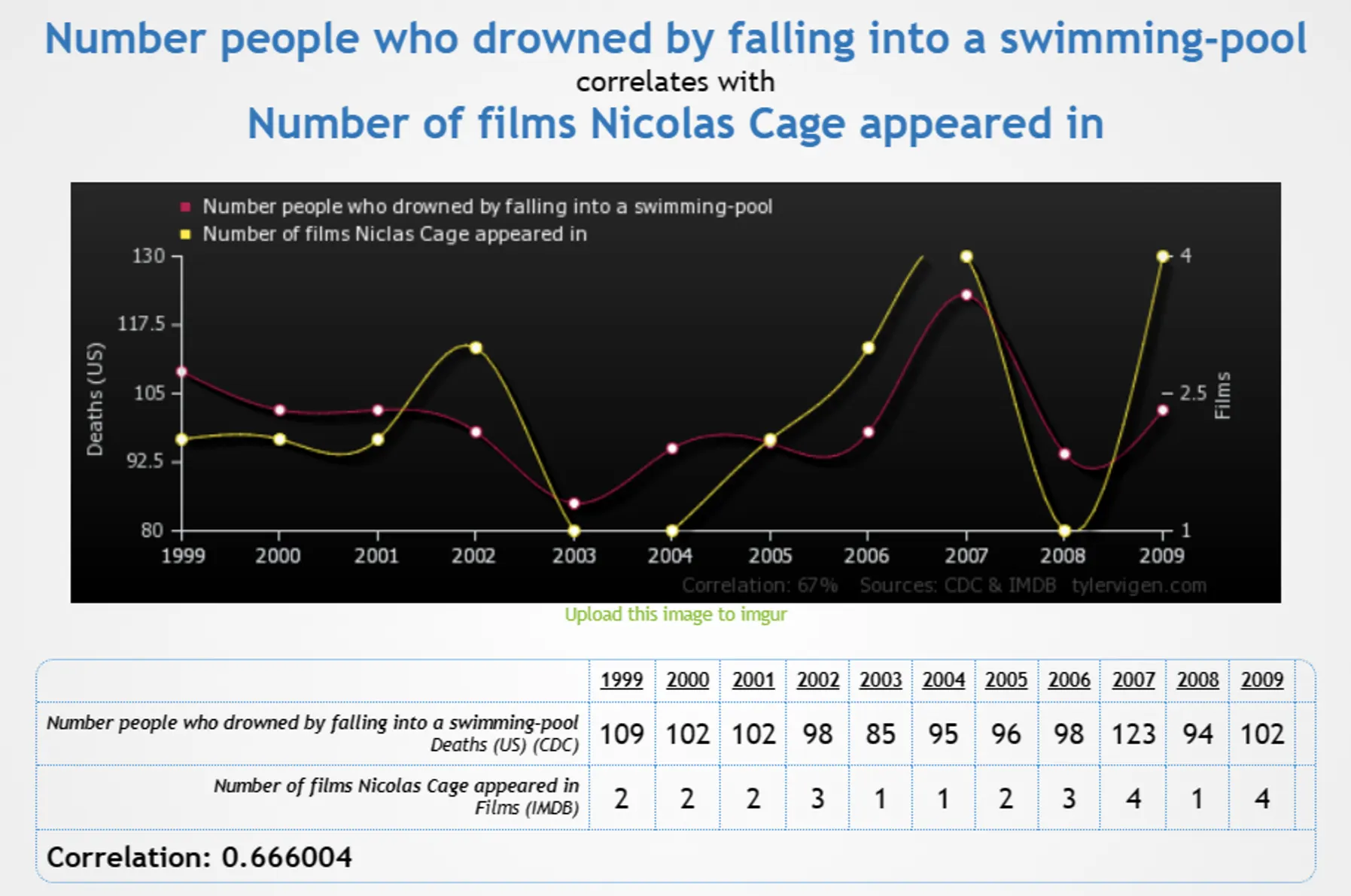
엄청나게 강한 상관관계를 가지고 있는 것처럼 보이지만, 그 결과를 설명하는 어떤한 원인가설도 없는 경우(인과 관계를 설명할 수 없는 경우)를 허위 상관관계라고 말함
•
근본적인 추세를 가진 데이터 → 정상 시계열보다 정보가 더 많기 때문에 여러 데이터가 함께 움직일 가능성이 높음
•
계절성을 가진 데이터 → 핫도그 소비와 익사(여름) 사이의 허위 상관관계
•
시간이 지나면서 변한 데이터의 수준이나 경사의 이동 → 무의미하게 높은 상관관계를 가진, 아령처럼 생긴 분포도를 생성
•
누적 합계 → 상관관계를 실제보다 더 좋아 보이게 만들기 위한 속임수로 사용
수영장에 빠져 익사한 사람 수와 니콜라스 케이지가 출연한 영화 수의 허위 상관
공적분(Cointegration)과의 관계
두 시계열 사이의 진짜 관계
•
공적분과 허위 상관 모두 높은 상관관계가 관측되어 이를 구별하는 것은 어려움
•
허위 상관은 어떤 관계도 없어도 되지만, 공적분 시계열은 서로 밀접한 관련성을 가짐
ex) ‘술 취한 사람과 그의 강아지’
3.3 유용한 시각화
•
데이터 시각화 : 데이터 분석 결과를 시각적으로 명확하게 표현하고 의사소통하는 것
◦
데이터를 한 눈에 이해할 수 있도록 함.
→ 시계열의 완벽한 탐색적 분석의 핵심은 그래프이다.
•
데이터 시각화의 효과
◦
분석할 때, 방대한 데이터에서 이상치, 패턴 등 주요 정보를 발견할 때 용이함.
◦
공유할 때, 사용자의 흥미 유발 및 몰입도를 제고시킬 수 있음.
따라서, 일반적인 질문의 해답을 구할 수 있는 방향의 시각화가 필요함.
•
복잡도에 따라 활용할 수 있는 다양한 시각화 기법
◦
종합적인 시간 분포도를 이해하기 위한 1차원 시각화
◦
시간에 따른 여러 측정치의 전형적인 궤적을 이해하기 위한 2차원 히스토그램
◦
두 개의 차원을 차지하는 시간, 또는 차원을 전혀 차지하지 않지만 내재된 시간에 대한 3차원 시각화
+ 데이터
3.3.1 1차원 시각화
여러 측정의 구성 단위가 있는 경우 시계열을 동시에 고려해야 함.
•
시각적으로 누적하여 시간에 따른 개별 분석 단위 강조하기
•
전체 회원을 대상으로 ‘붐비는’ 시기를 나타내거나 특정 회원의 ‘전체 활동 기간’ 중 활발했던 기간의 분포를 감각적으로 얻을 수 있음.
→ 간트 차트 : 프로젝트 일정관리를 위한 바(bar) 형태의 도구
# install.packages("timevis")
# Gantt Chart
require(timevis)
library("data.table")
donations <- fread("donations.csv")
d <- donations[, .(min(timestamp), max(timestamp)), user]
names(d) <- c("content", "start", "end")
d <- d[start != end]
timevis(d[sample(1:nrow(d), 20)])
R
복사
timevis(d[sample(1:nrow(d), 20)])
R
복사
‘timevis’ 함수는 d 데이터 프레임에 포함된 임의의 20개 행을 샘플링한 다음 시각화함.
→ 시간에 따라 데이터를 표시할 수 있는 대화형 시각화 도구를 사용하여 이루어짐.(간트 차트)
(프로젝트 관리에 유용한 차트임. 하나 이상 측정된 과정을 위한 시계열 분석에도 유용하게 사용됨.)
장점
1.
작업을 시간 및 수량적으로 일목요연하게 표시
2.
작업계획과 실적의 계속적 파악 용이
3.
작업자별, 부문별 업무성과의 객관적 상호 비교 가능
단점
1.
계획변화 및 변경 어려움.
2.
복잡하고 정밀한 일정계획 수립 어려움.
3.
작업상호간의 유기적인 관련성 파악 어려움.
4.
사전 예측 및 사후 통제 곤란
3.3.2 2차원 시각화
→ python으로 재구성
시간이 한 개 이상의 축에서 나타나는 특별한 경우
→ 매일, 매년 앞으로 나아가는 시간축과 시간, 요일 등에 따라서 시간을 펼쳐보는 경우
•
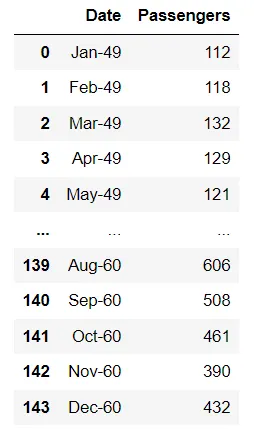
AirPassengers 데이터를 활용하여 계절성과 추세를 살펴보기
◦
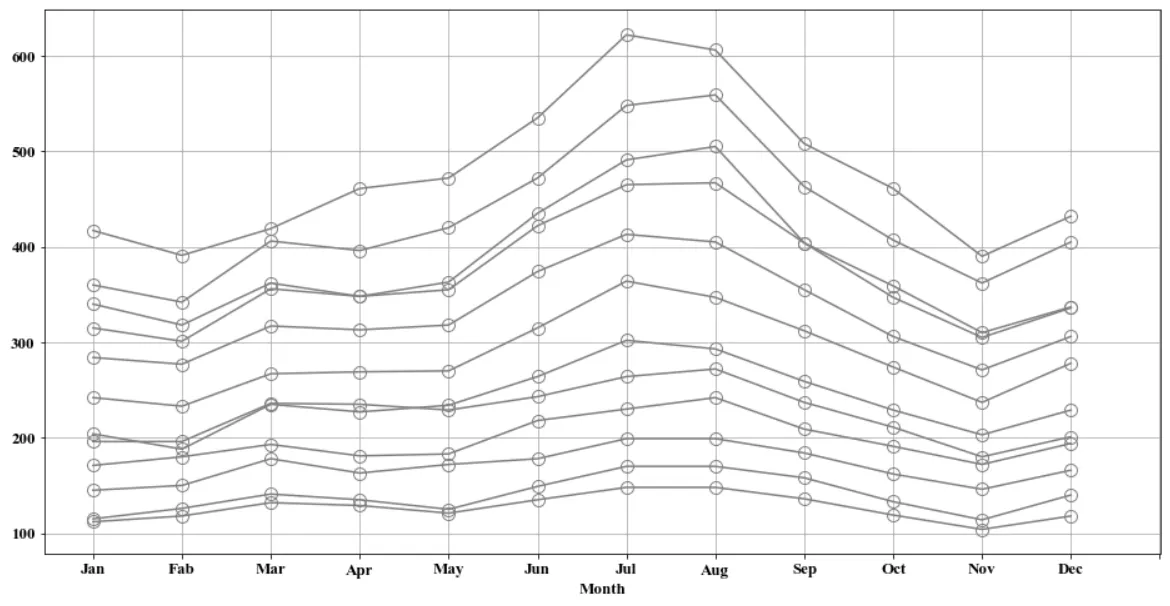
월의 진행을 반영하는 축에 기반하여 각 연도의 도표 그리기
t(matrix(AirPassengers, nrow = 12, ncol = 12))
R
복사
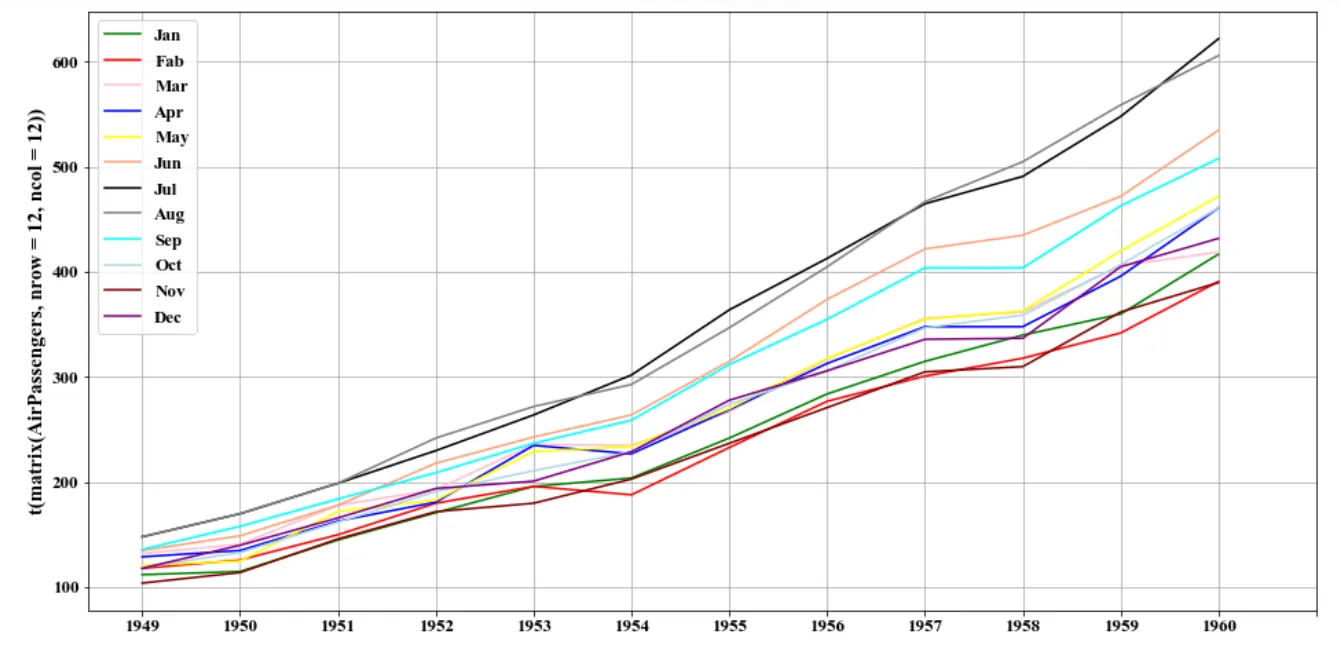
colors<-c("green","red", "pink", "blue",
"yellow","lightsalmon", "black", "gray",
"cyan", "lightblue", "maroon", "purple")
matplot(matrix(AirPassengers, nrow = 12, ncol = 12),
type = 'l', col = colors, lty = 1, lwd = 2.5,
xaxt = "n", ylab = "Passenger Count")
legend("topleft", legend = 1949:1960, lty = 1, lwd = 2.5,
col = colors)
axis(1, at = 1:12, labels = c("Jan", "Feb", "Mar", "Apr",
"May", "Jun", "Jul", "Aug",
"Sep", "Oct", "Nov", "Dec"))
R
복사
◦
오류가 발생하여 진행안됨. → Python으로 진행
Pass_mat = Pass_val.reshape([12,12])
Python
복사
Date_lab = ["Jan", "Fab", "Mar", "Apr", "May","Jun", "Jul","Aug",
"Sep", "Oct", "Nov", "Dec"]
plt.rcParams['font.family'] = 'TImes New Roman'
plt.rcParams['font.size'] = 13
fig = plt.figure(figsize=(16, 8))
ax = fig.add_subplot(1, 1, 1)
ax.grid(True)
for i in range(Pass_Trans.shape[0]):
ax.plot(Pass_Trans[:,i], color = Color_map[i])
ax.xaxis.set_major_locator(plt.MaxNLocator(12))
ax.set_xticks(np.arange(0, len(Pass_Trans)+1))
ax.set_xticklabels(Date_lab)
ax.set_ylabel("Passenger Count", Fontsize = 13)
ax.legend(np.arange(1949, 1961,1), loc='upper left')
Python
복사
•
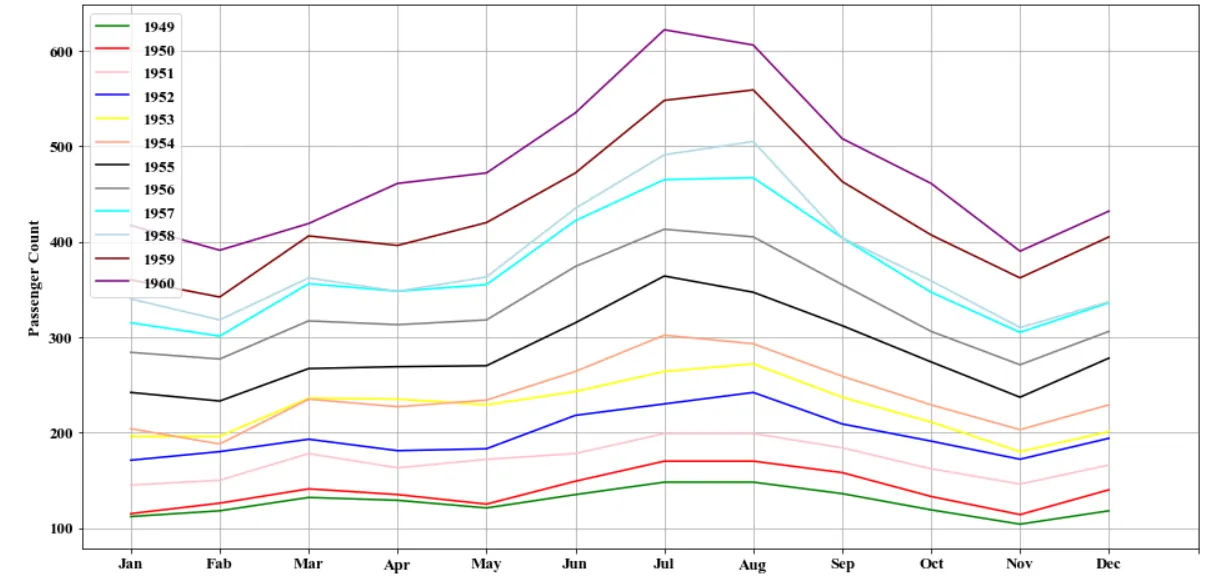
모든 연도가 공유하는 month에 대해 정의한 그래프
◦
항공 여객 수의 최고치는 7월 또는 8월에 기록됨.
◦
대부분 연도의 3월은 국소적 최고치를 보임.
•
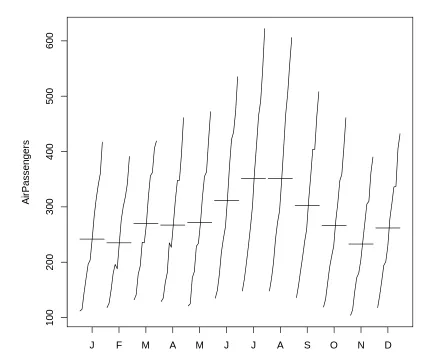
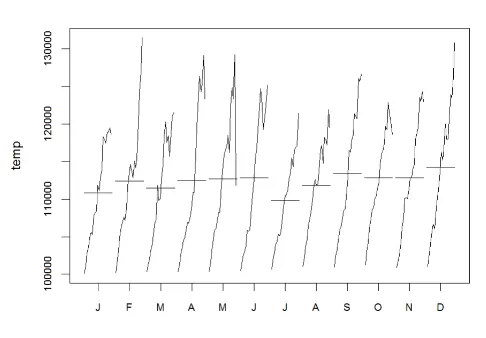
연도별 월별 곡선 도표
•
각 month에 대해 1949~1960년도에 대한 그래프 그리기
◦
월 별 탑승객 수와 연도 별 탑승객 증가 추세를 한 번에 확인
→ monthplot() 함수를 활용함 : 시계열 데이터의 월별 패턴 시각화
계절성이나 월별 변동성을 이해하는 데 도움이 됨.
1월과 7월 사이에 감소하는 추세를 볼 수 있음.
•
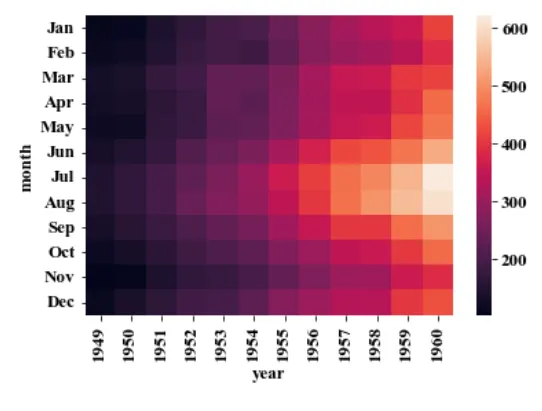
시계열 문맥에서 한 축은 시간, 다른 한 축은 관심 분야 단위로 구성된 2차원 히스토그램 그리기
◦
데이터의 구간을 나누어 구간화된 히트맵을 생성함.
◦
다중 시계열 데이터를 한 눈에 확인할 수 있음. / 계절성을 파악하는 데 활용함.
▪
Ex. 기준 [0, 10, 20, 30] / 데이터 [2, 13, 8, 27, 11]
→ 출력 값 [1, 2, 1, 3, 2]
np.searchsorted()
•
충분한 데이터가 없는 경우 해당 도표는 유용하게 사용되지 않음.
heatmap의 다양한 표현
•
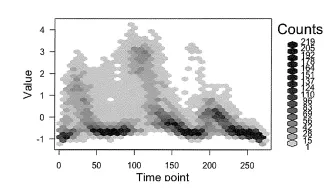
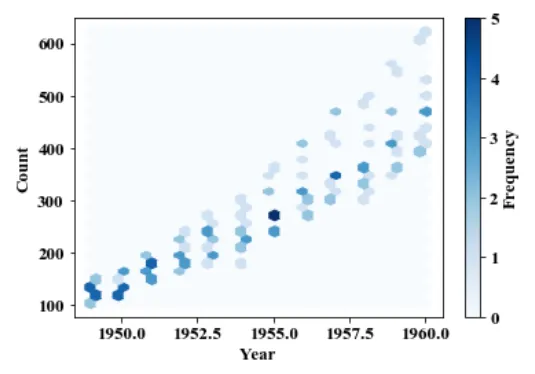
hexbin 메서드는 육각형의 그리드형태로 값을 반환하는 그래프이다.
w1<- words[V1== 1]
names(w1)<- c("type", 1:270)w1<- melt(w1,id.vars= "type")
w1<- w1[,-1]names(w1)<- c("Time point", "Value")
plot(hexbin(w1))
R
복사
plt.hexbin(f, df.values, gridsize = 30, cmap = "Blues")
plt.xlabel("Year")
plt.ylabel("Count")
plt.colorbar(label = 'Frequency')
Python
복사
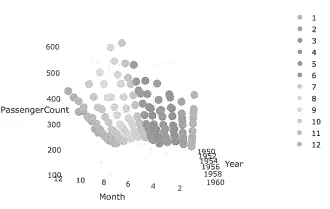
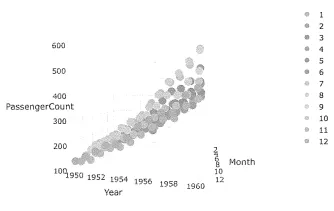
3.3.3 3차원 시각화
→ python으로 재구성
•
3차원 시각화 : 전체적인 윤곽을 이해하는 데 도움이 됨.
◦
소량의 데이터는 3차원으로 확장된 산점도로 표현하는 것이 2차원 히스토그램으로 표현하는 것보다 데이터의 윤곽을 이해하는 데 도움을 줄 수 있음.
◦
차원이 한 개 더 있는 만큼 다양한 시각에서 데이터의 분포를 확인할 수 있음.
require(plotly)
require(data.table)
months = 1:12
ap = data.table(matrix(AirPassengers, nrow = 12, ncol = 12))
names(ap) = as.character(1949:1960)
ap[, month := months]
ap = melt(ap, id.vars = 'month')
names(ap) = c("month", "year", "count")
p <- plot_ly(ap, x = ~month, y = ~year, z = ~count,
color = ~as.factor(month)) %>%
add_markers()%>%
layout(scene=list(xaxis = list(title = 'Month'),
yaxis = list(title = 'Year'),
zaxis = list(title = 'PassengerCount')))
JavaScript
복사
melt() 함수를 사용하여 데이터를 재구성합니다. 이를 통해 연도와 월에 따른 항공 여객 수를 담은 데이터 프레임을 만듦.
•
Python 사용한 3D 산점도 생성 및 데이터 시각화 예시
import plotly.graph_objects as go
import pandas as pd
import plotly.express as px
# Assuming AirPassengers data is already available in Python
# Create a DataFrame
months = list(range(1, 13))
ap = df
# Melt the DataFrame
ap_melted = pd.melt(ap.reset_index(), id_vars='month', var_name='year', value_name='count')
ap_melted.columns = ['month', 'year', 'count']
# Convert month and year to categorical variables
ap_melted['month'] = ap_melted['month'].astype('category')
ap_melted['year'] = ap_melted['year'].astype('category')
# Create 3D scatter plot
fig = go.Figure(data=[go.Scatter3d(
x=ap_melted['month'],
y=ap_melted['year'],
z=ap_melted['count'],
mode='markers',
marker=dict(
size=5,
# color=ap_melted['month'], # Color by month
colorscale='Viridis', # You can change the colorscale if needed
opacity=0.8
)
)])
# Update layout
fig.update_layout(scene=dict(
xaxis_title='Month',
yaxis_title='Year',
zaxis_title='Passenger Count'
))
fig.show()
Python
복사
•
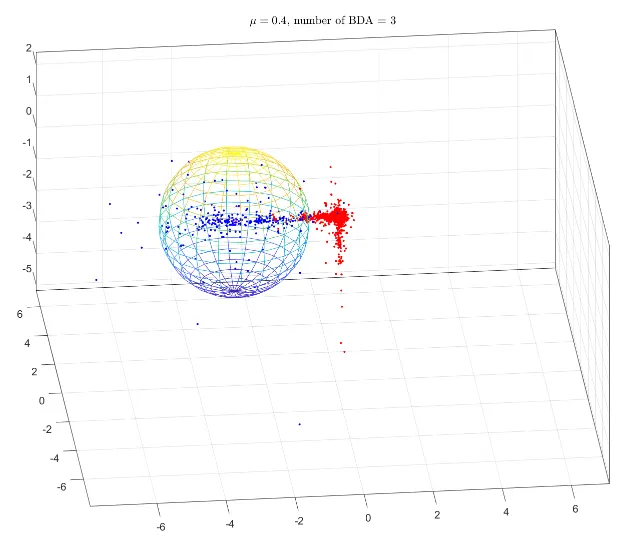
시계열 데이터가 아닌 경우, 데이터 분류를 위한 분포 확인 예시 → Matlab
시계열의 탐색적 자료 분석 [참고]
자기상관(autocorrelation 또는 series correlation)
어떤 신호(시계열)와 그 신호를 지연 이동한(time-lagged) 신호간의 상관관계
•
•
교차상관(cross-correlation)
◦
교차상관 분석 예
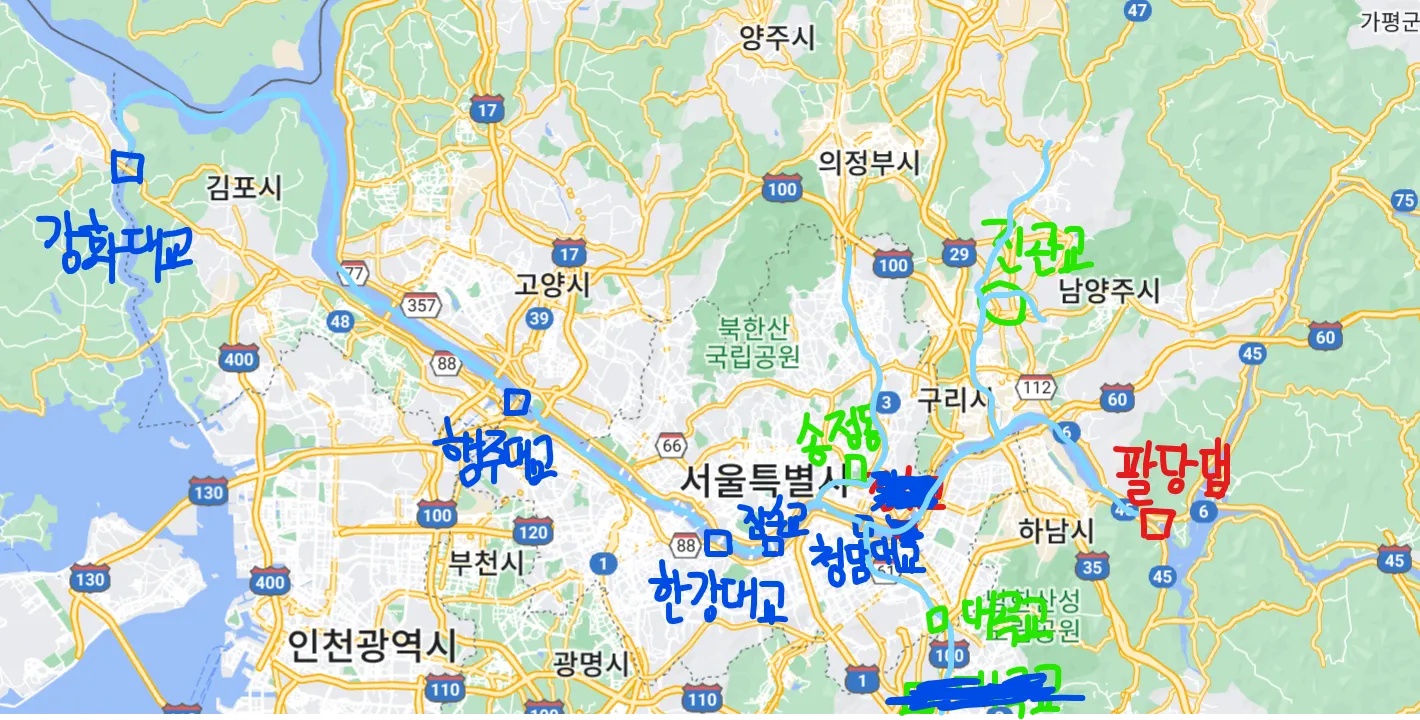
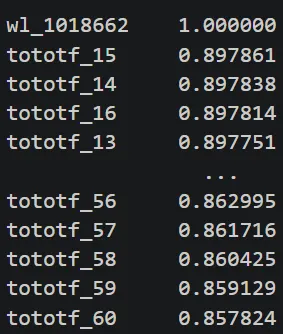
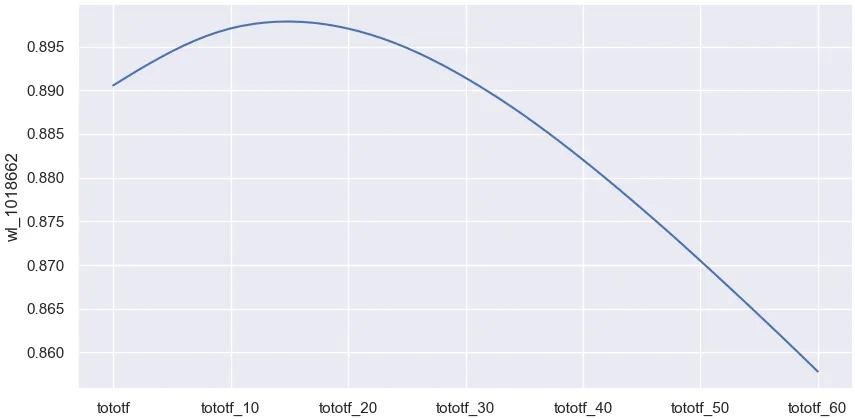
팔당댐 방류량과 청담대교 수위간의 CCF(Cross-Correlation Function) 결과
◦
15시간 전 방류량(tototf)이 청담대교 수위와 상관성이 가장 높았음
편자기상관함수(PACF: partial autocorrelation function) : 시간 효과(추세, 계절성)를 제거하는 방식의 자기상관함수
공적분(cointegration): 허위상관성이 아닌 두 시계열의 연관성(또는 인과관계)을 보여주는 통계적 지표
•
비유: 산책하는 집주인과 강아지의 이동 경로